Exponential growth
Encyclopedia
Exponential growth occurs when the growth rate of a mathematical function is proportional
to the function's current value. In the case of a discrete domain of definition with equal intervals it is also called geometric growth or geometric decay (the function values form a geometric progression
).
The exponential growth model is also known as the Malthusian growth model
. US scholar Albert Bartlett
pointed out the difficulty to grasp ramifications of exponential growth, stating: "The greatest shortcoming of the human race is our inability to understand the exponential function."
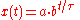
where the constant a is the initial value of x,
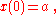
and the constant b is a positive growth factor, and τ is the time required for x to increase by a factor of b:
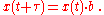
If τ > 0 and b > 1, then x has exponential growth. If τ < 0 and b > 1, or τ > 0 and 0 < b < 1, then x has exponential decay.
Example: If a species of bacteria doubles every ten minutes, starting out with only one bacterium, how many bacteria would be present after one hour? The question implies a = 1, b = 2 and τ = 10 min.
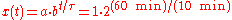
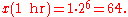
After one hour, or six ten-minute intervals, there would be sixty-four bacteria.
Many pairs (b, τ) of a dimensionless non-negative number b and an amount of time τ (a physical quantity
which can be expressed as the product of a number of units and a unit of time) represent the same growth rate, with τ proportional to log b. For any fixed b not equal to 1 (e.g. e or 2), the growth rate is given by the non-zero time τ. For any non-zero time τ the growth rate is given by the dimensionless positive number b.
Thus the law of exponential growth can be written in different but mathematically equivalent forms, by using a different base
. The most common forms are the following:
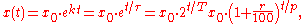
where x0 expresses the initial quantity x(0).
Parameters (negative in the case of exponential decay):
The quantities k,
, and T, and for a given p also r, have a one-to-one connection given by the following equation (which can be derived by taking the natural logarithm of the above):
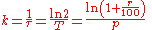
where k = 0 corresponds to r = 0 and to
and T being infinite.
If p is the unit of time the quotient t/p is simply the number of units of time. Using the notation t for the (dimensionless) number of units of time rather than the time itself, t/p can be replaced by t, but for uniformity this has been avoided here. In this case the division by p in the last formula is not a numerical division either, but converts a dimensionless number to the correct quantity including unit.
A popular approximated method for calculating the doubling time from the growth rate is the rule of 70,
i.e.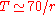
.
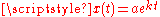satisfies the linear differential equation
:
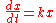
saying that the growth rate of x at time t is proportional to the value of x(t), and it has the initial value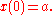
For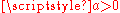
the differential equation is solved by the method of separation of variables
:
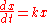
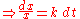
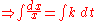
Incorporating the initial value gives:
The solution also applies for
where the logarithm is not defined.
For a nonlinear variation of this growth model see logistic function
.
) as well as any polynomial
growth, i.e., for all α:
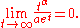
There is a whole hierarchy of conceivable growth rates that are slower than exponential and faster than linear (in the long run). See Degree of a polynomial#The degree computed from the function values.
Growth rates may also be faster than exponential.
In the above differential equation, if k < 0, then the quantity experiences exponential decay.
factors become significant (leading to a logistic growth model) or other underlying assumptions of the exponential growth model, such as continuity or instantaneous feedback, break down.
According to legend, a courtier presented the Persian king with a beautiful, hand-made chessboard
. The king asked what he would like in return for his gift and the courtier surprised the king by asking for one grain of rice on the first square, two grains on the second, four grains on the third etc. The king readily agreed and asked for the rice to be brought. All went well at first, but the requirement for 2 n − 1 grains on the nth square demanded over a million grains on the 21st square, more than a million million (aka trillion) on the 41st and there simply was not enough rice in the whole world for the final squares. (From Meadows et al. 1972, p. 29 via Porritt 2005)
For variation of this see second half of the chessboard in reference to the point where an exponentially growing factor begins to have a significant economic impact on an organization's overall business strategy.
French children are told a story in which they imagine having a pond with water lily
leaves floating on the surface. The lily population doubles in size every day and if left unchecked will smother the pond in 30 days, killing all the other living things in the water. Day after day the plant seems small and so it is decided to leave it to grow until it half-covers the pond, before cutting it back. They are then asked, on what day that will occur. This is revealed to be the 29th day, and then there will be just one day to save the pond. (From Meadows et al. 1972, p. 29 via Porritt 2005)
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
to the function's current value. In the case of a discrete domain of definition with equal intervals it is also called geometric growth or geometric decay (the function values form a geometric progression
Geometric progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
).
The exponential growth model is also known as the Malthusian growth model
Malthusian growth model
The Malthusian growth model, sometimes called the simple exponential growth model, is essentially exponential growth based on a constant rate of compound interest...
. US scholar Albert Bartlett
Albert Bartlett
Albert Allen Bartlett is an emeritus Professor of Physics at the University of Colorado at Boulder, USA. Professor Bartlett has lectured over 1,600 times since September, 1969 on Arithmetic, Population, and Energy...
pointed out the difficulty to grasp ramifications of exponential growth, stating: "The greatest shortcoming of the human race is our inability to understand the exponential function."
Examples
- BiologyBiologyBiology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
- The number of microorganismMicroorganismA microorganism or microbe is a microscopic organism that comprises either a single cell , cell clusters, or no cell at all...
s in a cultureMicrobiological cultureA microbiological culture, or microbial culture, is a method of multiplying microbial organisms by letting them reproduce in predetermined culture media under controlled laboratory conditions. Microbial cultures are used to determine the type of organism, its abundance in the sample being tested,...
both will grow exponentially until an essential nutrient is exhausted. Typically the first organism splitsCell divisionCell division is the process by which a parent cell divides into two or more daughter cells . Cell division is usually a small segment of a larger cell cycle. This type of cell division in eukaryotes is known as mitosis, and leaves the daughter cell capable of dividing again. The corresponding sort...
into two daughter organisms, who then each split to form four, who split to form eight, and so on. - A virus (for example SARS, or smallpoxSmallpoxSmallpox was an infectious disease unique to humans, caused by either of two virus variants, Variola major and Variola minor. The disease is also known by the Latin names Variola or Variola vera, which is a derivative of the Latin varius, meaning "spotted", or varus, meaning "pimple"...
) typically will spread exponentially at first, if no artificial immunizationImmunizationImmunization, or immunisation, is the process by which an individual's immune system becomes fortified against an agent ....
is available. Each infected person can infect multiple new people. - Human populationWorld populationThe world population is the total number of living humans on the planet Earth. As of today, it is estimated to be billion by the United States Census Bureau...
, if the number of births and deaths per person per year were to remain at current levels (but also see logistic growth). - Many responses of living beings to stimuliStimulus (physiology)In physiology, a stimulus is a detectable change in the internal or external environment. The ability of an organism or organ to respond to external stimuli is called sensitivity....
, including human perceptionPerceptionPerception is the process of attaining awareness or understanding of the environment by organizing and interpreting sensory information. All perception involves signals in the nervous system, which in turn result from physical stimulation of the sense organs...
, are logarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
ic responses, which are the inverse of exponential responses; the loudnessLoudnessLoudness is the quality of a sound that is primarily a psychological correlate of physical strength . More formally, it is defined as "that attribute of auditory sensation in terms of which sounds can be ordered on a scale extending from quiet to loud."Loudness, a subjective measure, is often...
and frequencyFrequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
of soundSoundSound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
are perceived logarithmically, even with very faint stimulus, within the limits of perception. This is the reason that exponentially increasing the brightnessBrightnessBrightness is an attribute of visual perception in which a source appears to be radiating or reflecting light. In other words, brightness is the perception elicited by the luminance of a visual target...
of visual stimuliVisual perceptionVisual perception is the ability to interpret information and surroundings from the effects of visible light reaching the eye. The resulting perception is also known as eyesight, sight, or vision...
is perceived by humans as a linear increase, rather than an exponential increase. This has survival value. Generally it is important for the organisms to respond to stimuli in a wide range of levels, from very low levels, to very high levels, while the accuracyAccuracy and precisionIn the fields of science, engineering, industry and statistics, the accuracy of a measurement system is the degree of closeness of measurements of a quantity to that quantity's actual value. The precision of a measurement system, also called reproducibility or repeatability, is the degree to which...
of the estimationEstimationEstimation is the calculated approximation of a result which is usable even if input data may be incomplete or uncertain.In statistics,*estimation theory and estimator, for topics involving inferences about probability distributions...
of differences at high levels of stimulus is much less important for survival.
- The number of microorganism
- PhysicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
- Avalanche breakdownAvalanche breakdownAvalanche breakdown is a phenomenon that can occur in both insulating and semiconducting materials. It is a form of electric current multiplication that can allow very large currents within materials which are otherwise good insulators. It is a type of electron avalanche...
within a dielectricDielectricA dielectric is an electrical insulator that can be polarized by an applied electric field. When a dielectric is placed in an electric field, electric charges do not flow through the material, as in a conductor, but only slightly shift from their average equilibrium positions causing dielectric...
material. A free electronElectronThe electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
becomes sufficiently accelerated by an externally applied electrical field that it frees up additional electrons as it collides with atomAtomThe atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s or moleculeMoleculeA molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s of the dielectric media. These secondary electrons also are accelerated, creating larger numbers of free electrons. The resulting exponential growth of electrons and ions may rapidly lead to complete dielectric breakdown of the material. - Nuclear chain reactionNuclear chain reactionA nuclear chain reaction occurs when one nuclear reaction causes an average of one or more nuclear reactions, thus leading to a self-propagating number of these reactions. The specific nuclear reaction may be the fission of heavy isotopes or the fusion of light isotopes...
(the concept behind nuclear reactors and nuclear weapons). Each uraniumUraniumUranium is a silvery-white metallic chemical element in the actinide series of the periodic table, with atomic number 92. It is assigned the chemical symbol U. A uranium atom has 92 protons and 92 electrons, of which 6 are valence electrons...
nucleusAtomic nucleusThe nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
that undergoes fissionNuclear fissionIn nuclear physics and nuclear chemistry, nuclear fission is a nuclear reaction in which the nucleus of an atom splits into smaller parts , often producing free neutrons and photons , and releasing a tremendous amount of energy...
produces multiple neutronNeutronThe neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
s, each of which can be absorbed by adjacent uranium atoms, causing them to fission in turn. If the probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of neutron absorption exceeds the probability of neutron escape (a functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the shapeShapeThe shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
and massMassMass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of the uranium), k > 0 and so the production rate of neutrons and induced uranium fissions increases exponentially, in an uncontrolled reaction. "Due to the exponential rate of increase, at any point in the chain reaction 99% of the energy will have been released in the last 4.6 generations. It is a reasonable approximation to think of the first 53 generations as a latency period leading up to the actual explosion, which only takes 3–4 generations." - Positive feedbackPositive feedbackPositive feedback is a process in which the effects of a small disturbance on a system include an increase in the magnitude of the perturbation. That is, A produces more of B which in turn produces more of A. In contrast, a system that responds to a perturbation in a way that reduces its effect is...
within the linear range of electrical or electroacoustic amplificationAmplifierGenerally, an amplifier or simply amp, is a device for increasing the power of a signal.In popular use, the term usually describes an electronic amplifier, in which the input "signal" is usually a voltage or a current. In audio applications, amplifiers drive the loudspeakers used in PA systems to...
can result in the exponential growth of the amplified signal, although resonanceResonanceIn physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
effects may favor some component frequencies of the signal over others. - Heat transferHeat transferHeat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer...
experiments yield results whose best fit line are exponential decay curves.
- Avalanche breakdown
- EconomicsEconomicsEconomics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
- Economic growthEconomic growthIn economics, economic growth is defined as the increasing capacity of the economy to satisfy the wants of goods and services of the members of society. Economic growth is enabled by increases in productivity, which lowers the inputs for a given amount of output. Lowered costs increase demand...
is expressed in percentage terms, implying exponential growth. For example, U.S. GDP per capita has grown at an exponential rate of approximately two percent per year for two centuries. - Multi-level marketingMulti-level marketingMulti-level marketing is a marketing strategy in which the sales force is compensated not only for sales they personally generate, but also for the sales of others they recruit, creating a downline of distributors and a hierarchy of multiple levels of compensation...
. Exponential increases are promised to appear in each new level of a starting member's downline as each subsequent member recruits more people.
- Economic growth
- FinanceFinance"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
- Compound interestCompound interestCompound interest arises when interest is added to the principal, so that from that moment on, the interest that has been added also itself earns interest. This addition of interest to the principal is called compounding...
at a constant interest rate provides exponential growth of the capital. See also rule of 72Rule of 72In finance, the rule of 72, the rule of 70 and the rule of 69 are methods for estimating an investment's doubling time. The rule number is divided by the interest percentage per period to obtain the approximate number of periods required for doubling...
. - Pyramid schemePyramid schemeA pyramid scheme is a non-sustainable business model that involves promising participants payment or services, primarily for enrolling other people into the scheme, rather than supplying any real investment or sale of products or services to the public...
s or Ponzi schemePonzi schemeA Ponzi scheme is a fraudulent investment operation that pays returns to its investors from their own money or the money paid by subsequent investors, rather than from any actual profit earned by the individual or organization running the operation...
s also show this type of growth resulting in high profits for a few initial investors and losses among great numbers of investors.
- Compound interest
- Computer technologyComputerA computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
- Processing powerClock rateThe clock rate typically refers to the frequency that a CPU is running at.For example, a crystal oscillator frequency reference typically is synonymous with a fixed sinusoidal waveform, a clock rate is that frequency reference translated by electronic circuitry into a corresponding square wave...
of computers. See also Moore's lawMoore's LawMoore's law describes a long-term trend in the history of computing hardware: the number of transistors that can be placed inexpensively on an integrated circuit doubles approximately every two years....
and technological singularityTechnological singularityTechnological singularity refers to the hypothetical future emergence of greater-than-human intelligence through technological means. Since the capabilities of such an intelligence would be difficult for an unaided human mind to comprehend, the occurrence of a technological singularity is seen as...
(under exponential growth, there are no singularities. The singularity here is a metaphor.). - In computational complexity theoryComputational complexity theoryComputational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, computer algorithms of exponential complexity require an exponentially increasing amount of resources (e.g. time, computer memory) for only a constant increase in problem size. So for an algorithm of time complexity 2x, if a problem of size x = 10 requires 10 seconds to complete, and a problem of size x = 11 requires 20 seconds, then a problem of size x = 12 will require 40 seconds. This kind of algorithm typically becomes unusable at very small problem sizes, often between 30 and 100 items (most computer algorithms need to be able to solve much larger problems, up to tens of thousands or even millions of items in reasonable times, something that would be physically impossible with an exponential algorithm). Also, the effects of Moore's LawMoore's LawMoore's law describes a long-term trend in the history of computing hardware: the number of transistors that can be placed inexpensively on an integrated circuit doubles approximately every two years....
do not help the situation much because doubling processor speed merely allows you to increase the problem size by a constant. E.g. if a slow processor can solve problems of size x in time t, then a processor twice as fast could only solve problems of size x+constant in the same time t. So exponentially complex algorithms are most often impractical, and the search for more efficient algorithms is one of the central goals of computer science today. - Internet traffic growthHistory of the InternetThe history of the Internet starts in the 1950s and 1960s with the development of computers. This began with point-to-point communication between mainframe computers and terminals, expanded to point-to-point connections between computers and then early research into packet switching...
.
- Processing power
Basic formula
A quantity x depends exponentially on time t if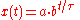where the constant a is the initial value of x,
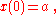
and the constant b is a positive growth factor, and τ is the time required for x to increase by a factor of b:
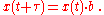
If τ > 0 and b > 1, then x has exponential growth. If τ < 0 and b > 1, or τ > 0 and 0 < b < 1, then x has exponential decay.
Example: If a species of bacteria doubles every ten minutes, starting out with only one bacterium, how many bacteria would be present after one hour? The question implies a = 1, b = 2 and τ = 10 min.
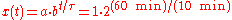
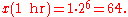
After one hour, or six ten-minute intervals, there would be sixty-four bacteria.
Many pairs (b, τ) of a dimensionless non-negative number b and an amount of time τ (a physical quantity
Physical quantity
A physical quantity is a physical property of a phenomenon, body, or substance, that can be quantified by measurement.-Definition of a physical quantity:Formally, the International Vocabulary of Metrology, 3rd edition defines quantity as:...
which can be expressed as the product of a number of units and a unit of time) represent the same growth rate, with τ proportional to log b. For any fixed b not equal to 1 (e.g. e or 2), the growth rate is given by the non-zero time τ. For any non-zero time τ the growth rate is given by the dimensionless positive number b.
Thus the law of exponential growth can be written in different but mathematically equivalent forms, by using a different base
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
. The most common forms are the following:
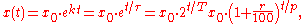
where x0 expresses the initial quantity x(0).
Parameters (negative in the case of exponential decay):
- The growth constant k is the frequencyFrequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
(number of times per unit time) of growing by a factor e; in finance it is also called the logarithmic return, continuously compounded return, or force of interest. - The e-folding timeE-foldingIn science, e-folding is the time interval in which an exponentially growing quantity increases by a factor of e. This term is often used in theoretical physics, especially when cosmic inflation is investigated...
is the time it takes to grow by a factor e. - The doubling timeDoubling timeThe doubling time is the period of time required for a quantity to double in size or value. It is applied to population growth, inflation, resource extraction, consumption of goods, compound interest, the volume of malignant tumours, and many other things which tend to grow over time...
T is the time it takes to double. - The percent increase r (a dimensionless number) in a period p.
The quantities k,
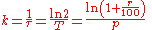
, and T, and for a given p also r, have a one-to-one connection given by the following equation (which can be derived by taking the natural logarithm of the above):where k = 0 corresponds to r = 0 and to
and T being infinite.If p is the unit of time the quotient t/p is simply the number of units of time. Using the notation t for the (dimensionless) number of units of time rather than the time itself, t/p can be replaced by t, but for uniformity this has been avoided here. In this case the division by p in the last formula is not a numerical division either, but converts a dimensionless number to the correct quantity including unit.
A popular approximated method for calculating the doubling time from the growth rate is the rule of 70,
i.e.
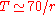.Differential equation
The exponential functionExponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
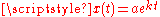satisfies the linear differential equationLinear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
:
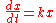
saying that the growth rate of x at time t is proportional to the value of x(t), and it has the initial value
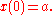
For
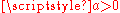the differential equation is solved by the method of separation of variablesSeparation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
:
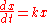
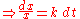
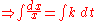
Incorporating the initial value gives:
The solution also applies for
where the logarithm is not defined.For a nonlinear variation of this growth model see logistic function
Logistic function
A logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P...
.
Other growth rates
In the long run, exponential growth of any kind will overtake linear growth of any kind (the basis of the Malthusian catastropheMalthusian catastrophe
A Malthusian catastrophe was originally foreseen to be a forced return to subsistence-level conditions once population growth had outpaced agricultural production...
) as well as any polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
growth, i.e., for all α:
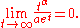
There is a whole hierarchy of conceivable growth rates that are slower than exponential and faster than linear (in the long run). See Degree of a polynomial#The degree computed from the function values.
Growth rates may also be faster than exponential.
In the above differential equation, if k < 0, then the quantity experiences exponential decay.
Limitations of models
Exponential growth models of physical phenomena only apply within limited regions, as unbounded growth is not physically realistic. Although growth may initially be exponential, the modelled phenomena will eventually enter a region in which previously ignored negative feedbackNegative feedback
Negative feedback occurs when the output of a system acts to oppose changes to the input of the system, with the result that the changes are attenuated. If the overall feedback of the system is negative, then the system will tend to be stable.- Overview :...
factors become significant (leading to a logistic growth model) or other underlying assumptions of the exponential growth model, such as continuity or instantaneous feedback, break down.
Rice on a chessboard
According to legend, a courtier presented the Persian king with a beautiful, hand-made chessboard
Chessboard
A chessboard is the type of checkerboard used in the board game chess, and consists of 64 squares arranged in two alternating colors...
. The king asked what he would like in return for his gift and the courtier surprised the king by asking for one grain of rice on the first square, two grains on the second, four grains on the third etc. The king readily agreed and asked for the rice to be brought. All went well at first, but the requirement for 2 n − 1 grains on the nth square demanded over a million grains on the 21st square, more than a million million (aka trillion) on the 41st and there simply was not enough rice in the whole world for the final squares. (From Meadows et al. 1972, p. 29 via Porritt 2005)
For variation of this see second half of the chessboard in reference to the point where an exponentially growing factor begins to have a significant economic impact on an organization's overall business strategy.
The water lily
French children are told a story in which they imagine having a pond with water lily
Nymphaeaceae
Nymphaeaceae is a family of flowering plants. Members of this family are commonly called water lilies and live in freshwater areas in temperate and tropical climates around the world. The family contains eight genera. There are about 70 species of water lilies around the world. The genus...
leaves floating on the surface. The lily population doubles in size every day and if left unchecked will smother the pond in 30 days, killing all the other living things in the water. Day after day the plant seems small and so it is decided to leave it to grow until it half-covers the pond, before cutting it back. They are then asked, on what day that will occur. This is revealed to be the 29th day, and then there will be just one day to save the pond. (From Meadows et al. 1972, p. 29 via Porritt 2005)
Sources
- Meadows, Donella H., Dennis L. Meadows, Jørgen Randers, and William W. Behrens III. (1972) The Limits to Growth. New York: University Books. ISBN 0-87663-165-0
- Porritt, J. Capitalism as if the world matters, Earthscan 2005. ISBN 1-84407-192-8
- Thomson, David G. Blueprint to a Billion: 7 Essentials to Achieve Exponential Growth, Wiley Dec 2005, ISBN 0-471-74747-5
- Tsirel, S. V. 2004. On the Possible Reasons for the Hyperexponential Growth of the Earth Population. Mathematical Modeling of Social and Economic Dynamics / Ed. by M. G. Dmitriev and A. P. Petrov, pp. 367–9. Moscow: Russian State Social University, 2004.
External links
- Exponent calculator — One of the best ways to see how exponents work is to simply try different examples. This calculator enables you to enter an exponent and a base number and see the result.
- Exponential Growth Calculator — This calculator enables you to perform a variety of calculations relating to exponential consumption growth.
- Understanding Exponential Growth — video clip 8.5 min
- Growth in a Finite World - Sustainability and the Exponential Function — Presentation
- Dr. Albert Bartlett: Arithmetic, Population and Energy — streaming video and audio 58 min