Rule of 72
Encyclopedia
In finance
, the rule of 72, the rule of 70 and the rule of 69 are methods for estimating an investment
's doubling time. The rule number is divided by the interest percentage per period to obtain the approximate number of periods (usually years) required for doubling. Although scientific calculator
s and spreadsheet
programs have functions to find the accurate doubling time, the rules are useful for mental calculation
s and when only a basic calculator
is available.
These rules apply to exponential growth
and are therefore used for compound interest
as opposed to simple interest calculations. They can also be used for decay to obtain a halving time. The choice of number is mostly a matter of preference, 69 is more accurate for continuous compounding, while 72 works well in common interest situations and is more easily divisible. Felix's Corollary provides a method of estimating the future value
of an annuity
using the same principles.
There are a number of variations to the rules that improve accuracy. For periodic compounding, the exact doubling time for an interest rate of r per period is: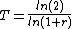
.
The formula above can be used for more than calculating the doubling time. If you want to know the tripling time, for example, simply replace the constant 2 in the numerator with 3. As another example, if you want to know the number of periods it takes for the initial value to rise by 50%, replace the constant 2 with 1.5.
Similarly, to determine the time it takes for the value of money to halve at a given rate, divide the rule quantity by that rate.
s: 1, 2, 3, 4, 6, 8, 9, and 12. It provides a good approximation for annual compounding, and for compounding at typical rates (from 6% to 10%). The approximations are less accurate at higher interest rates.
For continuous compounding, 69 gives accurate results for any rate. This is because ln
(2) is about 69.3%; see derivation below. Since daily compounding is close enough to continuous compounding, for most purposes 69, 69.3 or 70 are better than 72 for daily compounding. For lower annual rates than those above, 69.3 would also be more accurate than 72.
(1445–1514). He presents the rule in a discussion regarding the estimation of the doubling time of an investment, but does not derive or explain the rule, and it is thus assumed that the rule predates Pacioli by some time.
Roughly translated:
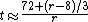
or for the same result, but simpler:
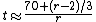
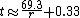
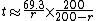
For example, if the interest rate is 18% the Rule of 69.3 says t = 3.85 years. The E-M Rule multiplies this by 200/(200-18), giving a doubling time of 4.23 years, where the actual doubling time at this rate is 4.19 years. (The E-M Rule thus gives a closer approximation than the Rule of 72.)
Note that if the numerator here is simply 69.3 times 200. As long as the product stays constant, the factors can be modified arbitrarily. The E-M rule could thus be written also as
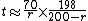or 
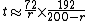
in order to keep the product mostly unchanged. In these variants, the multiplicative correction becomes 1 respectively for r=2 and r=8, the values for which the rule of 70 (respectively 72) is most precise.
Similarly, the 3rd-order Padé approximant
gives a more accurate answer over an even larger range of r, but it has a slightly more complicated formula:
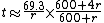
provides a method of approximating the future value
of an annuity
(a series of regular payments), using the same principles as the Rule of 72. The corollary states that future value of an annuity whose percentage interest rate and number of payments multiply to be 72 can be approximated by multiplying the sum of the payments by 1.5.
As an example, 12 periodic payments of $1000 growing at 6% per period will be worth approximately $18,000 after the last period. This can be calculated by multiplying the $12,000 of payments by 1.5. This is an application of Felix's corollary because 12 (= #periods) times 6 (= %interest) is 72. Likewise, 8 periodic thousand dollar payments at 9% will result in 1.5 times the $8000, or $12,000.
The equation is:
where:
Using Felix's corollary, one can estimate that by saving two-thirds of the total, in periodic deposits, the interest will take care of the rest (since 1.5 times two-thirds will equal the desired goal). So the goal becomes to set aside $720,000 in equal periodic deposits, such that it grows to approximate the target amount of $1,080,000.
is given by: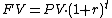
where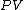
is the present value
,
is the number of time periods, and 
stands for the interest rate per time period.
The future value is double the present value when the following condition is met: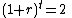
This equation is easily solved for
:
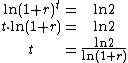
If
is small, then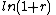 
approximately equals 
(this is the first term in the Taylor series). Together with the approximation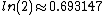 
, this gives: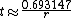
which improves in accuracy as the compounding of interest
becomes continuous (see derivation below).
However, humans tend to prefer performing mental calculations with percentage
s, so the formula is often restated as follows: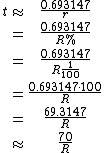
In order to derive the more precise adjustments presented above, it is noted that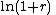
is more closely approximated by 
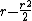(using the second term in the Taylor series
).
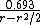can then be further simplified by Taylor approximations:
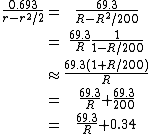
Replacing R/200 in the third line with 7.79 gives 72 on the numerator. This shows that the rule of 72 is most precise for periodically composed interests around 8%.
Alternatively, the E-M rule is obtained if the second-order Taylor approximation is used directly.
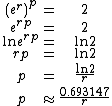
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, the rule of 72, the rule of 70 and the rule of 69 are methods for estimating an investment
Investment
Investment has different meanings in finance and economics. Finance investment is putting money into something with the expectation of gain, that upon thorough analysis, has a high degree of security for the principal amount, as well as security of return, within an expected period of time...
's doubling time. The rule number is divided by the interest percentage per period to obtain the approximate number of periods (usually years) required for doubling. Although scientific calculator
Scientific calculator
A scientific calculator is a type of electronic calculator, usually but not always handheld, designed to calculate problems in science, engineering, and mathematics...
s and spreadsheet
Spreadsheet
A spreadsheet is a computer application that simulates a paper accounting worksheet. It displays multiple cells usually in a two-dimensional matrix or grid consisting of rows and columns. Each cell contains alphanumeric text, numeric values or formulas...
programs have functions to find the accurate doubling time, the rules are useful for mental calculation
Mental calculation
Mental calculation comprises arithmetical calculations using only the human brain, with no help from calculators, computers, or pen and paper. People use mental calculation when computing tools are not available, when it is faster than other means of calculation , or in a competition context...
s and when only a basic calculator
Calculator
An electronic calculator is a small, portable, usually inexpensive electronic device used to perform the basic operations of arithmetic. Modern calculators are more portable than most computers, though most PDAs are comparable in size to handheld calculators.The first solid-state electronic...
is available.
These rules apply to exponential growth
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
and are therefore used for compound interest
Compound interest
Compound interest arises when interest is added to the principal, so that from that moment on, the interest that has been added also itself earns interest. This addition of interest to the principal is called compounding...
as opposed to simple interest calculations. They can also be used for decay to obtain a halving time. The choice of number is mostly a matter of preference, 69 is more accurate for continuous compounding, while 72 works well in common interest situations and is more easily divisible. Felix's Corollary provides a method of estimating the future value
Future value
Future value is the value of an asset at a specific date. It measures the nominal future sum of money that a given sum of money is "worth" at a specified time in the future assuming a certain interest rate, or more generally, rate of return; it is the present value multiplied by the accumulation...
of an annuity
Annuity (finance theory)
The term annuity is used in finance theory to refer to any terminating stream of fixed payments over a specified period of time. This usage is most commonly seen in discussions of finance, usually in connection with the valuation of the stream of payments, taking into account time value of money...
using the same principles.
There are a number of variations to the rules that improve accuracy. For periodic compounding, the exact doubling time for an interest rate of r per period is:
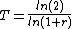.The formula above can be used for more than calculating the doubling time. If you want to know the tripling time, for example, simply replace the constant 2 in the numerator with 3. As another example, if you want to know the number of periods it takes for the initial value to rise by 50%, replace the constant 2 with 1.5.
Using the rule to estimate compounding periods
To estimate the number of periods required to double an original investment, divide the most convenient "rule-quantity" by the expected growth rate, expressed as a percentage.- For instance, if you were to invest $100 with compounding interest at a rate of 9% per annum, the rule of 72 gives 72/9 = 8 years required for the investment to be worth $200; an exact calculation gives 8.0432 years.
Similarly, to determine the time it takes for the value of money to halve at a given rate, divide the rule quantity by that rate.
- To determine the time for moneyMoneyMoney is any object or record that is generally accepted as payment for goods and services and repayment of debts in a given country or socio-economic context. The main functions of money are distinguished as: a medium of exchange; a unit of account; a store of value; and, occasionally in the past,...
's buying powerPurchasing powerPurchasing power is the number of goods/services that can be purchased with a unit of currency. For example, if you had taken one dollar to a store in the 1950s, you would have been able to buy a greater number of items than you would today, indicating that you would have had a greater purchasing...
to halve, financiers simply divide the rule-quantity by the inflation rateInflation rateIn economics, the inflation rate is a measure of inflation, the rate of increase of a price index . It is the percentage rate of change in price level over time. The rate of decrease in the purchasing power of money is approximately equal.The inflation rate is used to calculate the real interest...
. Thus at 3.5% inflationInflationIn economics, inflation is a rise in the general level of prices of goods and services in an economy over a period of time.When the general price level rises, each unit of currency buys fewer goods and services. Consequently, inflation also reflects an erosion in the purchasing power of money – a...
using the rule of 70, it should take approximately 70/3.5 = 20 years for the value of a unit of currency to halve.
- To estimate the impact of additional fees on financial policies (e.g., mutual fund fees and expensesMutual fund fees and expensesMutual fund fees and expenses are charges that may be incurred by investors who hold mutual funds. Running a mutual fund involves costs, including shareholder transaction costs, investment advisory fees, and marketing and distribution expenses...
, loading and expense charges on variable universal life insuranceVariable universal life insuranceVariable Universal Life Insurance is a type of life insurance that builds a cash value. In a VUL, the cash value can be invested in a wide variety of separate accounts, similar to mutual funds, and the choice of which of the available separate accounts to use is entirely up to the contract owner...
investment portfolios), divide 72 by the fee. For example, if the Universal Life policy charges a 3% fee over and above the cost of the underlying investment fund, then the total account value will be cut to 1/2 in 72 / 3 = 24 years, and then to just 1/4 the value in 48 years, compared to holding exactly the same investment outside the policy.
Choice of rule
The value 72 is a convenient choice of numerator, since it has many small divisorDivisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s: 1, 2, 3, 4, 6, 8, 9, and 12. It provides a good approximation for annual compounding, and for compounding at typical rates (from 6% to 10%). The approximations are less accurate at higher interest rates.
For continuous compounding, 69 gives accurate results for any rate. This is because ln
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
(2) is about 69.3%; see derivation below. Since daily compounding is close enough to continuous compounding, for most purposes 69, 69.3 or 70 are better than 72 for daily compounding. For lower annual rates than those above, 69.3 would also be more accurate than 72.
| Rate | Actual Years | Rule of 72 | Rule of 70 | Rule of 69.3 | 72 adjusted | E-M rule |
|---|---|---|---|---|---|---|
| 0.25% | 277.605 | 288.000 | 280.000 | 277.200 | 277.667 | 277.547 |
| 0.5% | 138.976 | 144.000 | 140.000 | 138.600 | 139.000 | 138.947 |
| 1% | 69.661 | 72.000 | 70.000 | 69.300 | 69.667 | 69.648 |
| 2% | 35.003 | 36.000 | 35.000 | 34.650 | 35.000 | 35.000 |
| 3% | 23.450 | 24.000 | 23.333 | 23.100 | 23.444 | 23.452 |
| 4% | 17.673 | 18.000 | 17.500 | 17.325 | 17.667 | 17.679 |
| 5% | 14.207 | 14.400 | 14.000 | 13.860 | 14.200 | 14.215 |
| 6% | 11.896 | 12.000 | 11.667 | 11.550 | 11.889 | 11.907 |
| 7% | 10.245 | 10.286 | 10.000 | 9.900 | 10.238 | 10.259 |
| 8% | 9.006 | 9.000 | 8.750 | 8.663 | 9.000 | 9.023 |
| 9% | 8.043 | 8.000 | 7.778 | 7.700 | 8.037 | 8.062 |
| 10% | 7.273 | 7.200 | 7.000 | 6.930 | 7.267 | 7.295 |
| 11% | 6.642 | 6.545 | 6.364 | 6.300 | 6.636 | 6.667 |
| 12% | 6.116 | 6.000 | 5.833 | 5.775 | 6.111 | 6.144 |
| 15% | 4.959 | 4.800 | 4.667 | 4.620 | 4.956 | 4.995 |
| 18% | 4.188 | 4.000 | 3.889 | 3.850 | 4.185 | 4.231 |
| 20% | 3.802 | 3.600 | 3.500 | 3.465 | 3.800 | 3.850 |
| 25% | 3.106 | 2.880 | 2.800 | 2.772 | 3.107 | 3.168 |
| 30% | 2.642 | 2.400 | 2.333 | 2.310 | 2.644 | 2.718 |
| 40% | 2.060 | 1.800 | 1.750 | 1.733 | 2.067 | 2.166 |
| 50% | 1.710 | 1.440 | 1.400 | 1.386 | 1.720 | 1.848 |
| 60% | 1.475 | 1.200 | 1.167 | 1.155 | 1.489 | 1.650 |
| 70% | 1.306 | 1.029 | 1.000 | 0.990 | 1.324 | 1.523 |
History
An early reference to the rule is in the Summa de Arithmetica (Venice, 1494. Fol. 181, n. 44) of Luca PacioliLuca Pacioli
Fra Luca Bartolomeo de Pacioli was an Italian mathematician, Franciscan friar, collaborator with Leonardo da Vinci, and seminal contributor to the field now known as accounting...
(1445–1514). He presents the rule in a discussion regarding the estimation of the doubling time of an investment, but does not derive or explain the rule, and it is thus assumed that the rule predates Pacioli by some time.
Roughly translated:
Adjustments for higher accuracy
For higher rates, a bigger numerator would be better (e.g. for 20%, using 76 to get 3.8 years would be only about 0.002 off, where using 72 to get 3.6 would be about 0.2 off). This is because, as above, the rule of 72 is only an approximation that is accurate for interest rates from 6% to 10%. Outside that range the error will vary from 2.4% to −14.0%. For every three percentage points away from 8% the value 72 could be adjusted by 1.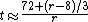or for the same result, but simpler:
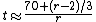
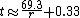
E-M rule
The Eckart-McHale second-order rule, the E-M rule, provides a multiplicative correction for the Rule of 69.3 that is very accurate for rates from 0%–20%. The Rule of 69.3 is normally only accurate at the lowest end of interest rates, from 0% to about 5%. To compute the E-M approximation, simply multiply the Rule of 69.3 result by 200/(200-r) as follows: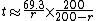For example, if the interest rate is 18% the Rule of 69.3 says t = 3.85 years. The E-M Rule multiplies this by 200/(200-18), giving a doubling time of 4.23 years, where the actual doubling time at this rate is 4.19 years. (The E-M Rule thus gives a closer approximation than the Rule of 72.)
Note that if the numerator here is simply 69.3 times 200. As long as the product stays constant, the factors can be modified arbitrarily. The E-M rule could thus be written also as
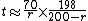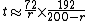
or in order to keep the product mostly unchanged. In these variants, the multiplicative correction becomes 1 respectively for r=2 and r=8, the values for which the rule of 70 (respectively 72) is most precise.
Similarly, the 3rd-order Padé approximant
Padé approximant
Padé approximant is the "best" approximation of a function by a rational function of given order - under this technique, the approximant's power series agrees with the power series of the function it is approximating....
gives a more accurate answer over an even larger range of r, but it has a slightly more complicated formula:
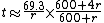
Felix's Corollary to the Rule of 72
Felix's CorollaryCorollary
A corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
provides a method of approximating the future value
Future value
Future value is the value of an asset at a specific date. It measures the nominal future sum of money that a given sum of money is "worth" at a specified time in the future assuming a certain interest rate, or more generally, rate of return; it is the present value multiplied by the accumulation...
of an annuity
Annuity (finance theory)
The term annuity is used in finance theory to refer to any terminating stream of fixed payments over a specified period of time. This usage is most commonly seen in discussions of finance, usually in connection with the valuation of the stream of payments, taking into account time value of money...
(a series of regular payments), using the same principles as the Rule of 72. The corollary states that future value of an annuity whose percentage interest rate and number of payments multiply to be 72 can be approximated by multiplying the sum of the payments by 1.5.
As an example, 12 periodic payments of $1000 growing at 6% per period will be worth approximately $18,000 after the last period. This can be calculated by multiplying the $12,000 of payments by 1.5. This is an application of Felix's corollary because 12 (= #periods) times 6 (= %interest) is 72. Likewise, 8 periodic thousand dollar payments at 9% will result in 1.5 times the $8000, or $12,000.
The equation is:
-
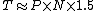when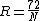 
where:
-
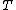is the total ending balance. -
is the periodic payment amount. -
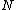is the number of payments. -
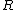is the interest rate multiplied by 
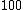; that is, the interest rate can be expressed as 
per period.
Accuracy
Felix's Corollary has accuracy issues similar to the Rule of 72; it is reasonably accurate in the 6% to 12% range (especially in the 8% to 9% range), and progressively loses accuracy at smaller or larger values. In addition, an adjustment needs to be considered in the cases where non-integer payments are required (such as at 7% or 10% or 12.5% interest). In such cases, a fractional last payment must be made as you would expect. As an example, at 10% interest, 7.2 periodic payments must be made. In normal cases, whole payments are made at the beginning of a period. It's not entirely obvious as to when the .2 payment must be made. But for purposes of approximation, the corollary works quite well.Millionaire's estimation
The millionaire's estimation is a simple savings calculator, posing the question "How much must I save per year to have saved $1,080,000?" Of course, the annual interest rate is a factor. In the original challenge, the number $1,080,000 was chosen because it is divisible by 72.Using Felix's corollary, one can estimate that by saving two-thirds of the total, in periodic deposits, the interest will take care of the rest (since 1.5 times two-thirds will equal the desired goal). So the goal becomes to set aside $720,000 in equal periodic deposits, such that it grows to approximate the target amount of $1,080,000.
| Rate of Interest (given) |
Periods, (calculated 72/Rate) |
Savings Required per Period, (calculated $720,000/Periods or Rate pct x $1MM) |
Amount Saved |
Actual Interest Accumulated |
Total |
|---|---|---|---|---|---|
| 2% | 36 | $20,000 | $720,000 | $340,685.09 | $1,060,685.09 |
| 4% | 18 | $40,000 | $720,000 | $346,849.18 | $1,066,849.18 |
| 6% | 12 | $60,000 | $720,000 | $352,928.26 | $1,072,928.26 |
| 8% | 9 | $80,000 | $720,000 | $358,925.00 | $1,078,925.00 |
| 9% | 8 | $90,000 | $720,000 | $361,893.28 | $1,081,893.28 |
| 12% | 6 | $120,000 | $720,000 | $370,681.41 | $1,090,681.41 |
Other Rules
Extending the Rule of 72 out further, other approximations can be determined for tripling and quadrupling. To estimate the time it would take to triple your money, one can use 114 instead of 72. And for quadrupling, use 144.Periodic compounding
For periodic compounding, future valueFuture value
Future value is the value of an asset at a specific date. It measures the nominal future sum of money that a given sum of money is "worth" at a specified time in the future assuming a certain interest rate, or more generally, rate of return; it is the present value multiplied by the accumulation...
is given by:
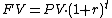
where
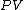is the present valuePresent value
Present value, also known as present discounted value, is the value on a given date of a future payment or series of future payments, discounted to reflect the time value of money and other factors such as investment risk...
,
is the number of time periods, and stands for the interest rate per time period.The future value is double the present value when the following condition is met:
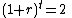
This equation is easily solved for
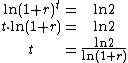
:If
is small, then 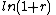approximately equals (this is the first term in the Taylor series). Together with the approximation 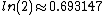, this gives: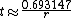which improves in accuracy as the compounding of interest
Compound interest
Compound interest arises when interest is added to the principal, so that from that moment on, the interest that has been added also itself earns interest. This addition of interest to the principal is called compounding...
becomes continuous (see derivation below).
However, humans tend to prefer performing mental calculations with percentage
Percentage
In mathematics, a percentage is a way of expressing a number as a fraction of 100 . It is often denoted using the percent sign, “%”, or the abbreviation “pct”. For example, 45% is equal to 45/100, or 0.45.Percentages are used to express how large/small one quantity is, relative to another quantity...
s, so the formula is often restated as follows:
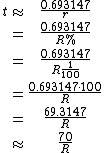
In order to derive the more precise adjustments presented above, it is noted that
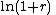is more closely approximated by 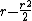(using the second term in the Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
).
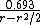can then be further simplified by Taylor approximations: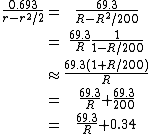Replacing R/200 in the third line with 7.79 gives 72 on the numerator. This shows that the rule of 72 is most precise for periodically composed interests around 8%.
Alternatively, the E-M rule is obtained if the second-order Taylor approximation is used directly.
Continuous compounding
For continuous compounding, the derivation is simpler: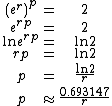See also
- Exponential growthExponential growthExponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
- Time value of moneyTime value of moneyThe time value of money is the value of money figuring in a given amount of interest earned over a given amount of time. The time value of money is the central concept in finance theory....
- InterestInterestInterest is a fee paid by a borrower of assets to the owner as a form of compensation for the use of the assets. It is most commonly the price paid for the use of borrowed money, or money earned by deposited funds....
- Discount
- Rule of 16Volatility (finance)In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
External links
- The Scales Of 70 – extends the rule of 72 beyond fixed-rate growth to variable rate compound growth including positive and negative rates.
- A note on the rule of 72 or how long it takes to double your money, The Investment Analysts Society of South AfricaInvestment Analysts Society of Southern AfricaThe Investment Analyst's Society of Southern Africa is the liaison body for the financial analyst profession in South Africa. It is based in Johannesburg South Africa, with members from Cape Town, Durban and throughout the region.-Membership:...
- Rule of 72 Calculator, moneychimp.com
- Rule of 72 Learning Tool, directinvesting.com