Padé approximant
Encyclopedia
Padé approximant is the "best" approximation of a function by a rational function
of given order - under this technique, the approximant's power series agrees with the power series of the function it is approximating.
The technique was developed by Henri Padé
, but goes back to Georg Frobenius who introduced the idea and investigated the features of rational approximations of power series.
The Padé approximant often gives better approximation of the function than truncating its Taylor series
, and it may still work where the Taylor series does not converge. For these reasons Padé approximants are used extensively in computer calculation
s. They have also been used as auxiliary function
s in Diophantine approximation
and transcendental number theory
, though for sharp results ad hoc methods in some sense inspired by the Padé theory typically replace them.
s m ≥ 0 and n ≥ 0, the Padé approximant of order [m/n] is the rational function
which agrees with
to the highest possible order, which amounts to
.
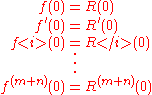Equivalently, if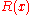
is expanded in a Maclaurin series (Taylor series
at 0), its first m + n terms would cancel the first m + n terms of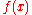
, and as such:
The Padé approximant is unique for given m and n, that is, the coefficients
can be uniquely determined. It is for reasons of uniqueness that the zero-th order term at the denominator of 
was chosen to be 1, otherwise the numerator and denominator of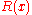 
would have been unique only up to
multiplication by a constant.
The Padé approximant defined above is also denoted as
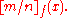
For given
, Padé approximants can be computed by Wynn
's epsilon algorithm and also other sequence transformations from the partial sums
of the Taylor series
of
, i.e., we have
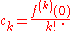
can also be a formal power series
, and, hence, Padé approximants can also be applied to the summation of divergent series
.
, say
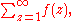
it can be useful to introduce the Padé or simply rational zeta function as
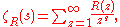
where
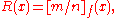
is just the Padé approximation of order (m, n) of the function f(x). The zeta regularization value at s = 0 is taken to be the sum of the divergent series.
The functional equation for this Padé zeta function is
where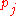
and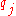 
are the coefficients in the Padé approximation. The subscript '0' means that the Padé is of order [0/0] and hence, we got the Riemann zeta function.
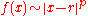, one calls x = r a critical point and p the associated critical exponent of f. If sufficient terms of the series expansion of f are known, one can approximately extract the critical points and the critical exponents from respectively the poles and residues of the Padé approximants 
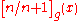where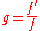 
.
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
of given order - under this technique, the approximant's power series agrees with the power series of the function it is approximating.
The technique was developed by Henri Padé
Henri Padé
Henri Eugène Padé was a French mathematician, who is now remembered mainly for his development of approximation techniques for functions using rational functions.He was educated at École Normale Supérieure in Paris...
, but goes back to Georg Frobenius who introduced the idea and investigated the features of rational approximations of power series.
The Padé approximant often gives better approximation of the function than truncating its Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
, and it may still work where the Taylor series does not converge. For these reasons Padé approximants are used extensively in computer calculation
Calculation
A calculation is a deliberate process for transforming one or more inputs into one or more results, with variable change.The term is used in a variety of senses, from the very definite arithmetical calculation of using an algorithm to the vague heuristics of calculating a strategy in a competition...
s. They have also been used as auxiliary function
Auxiliary function
In mathematics, auxiliary functions are an important construction in transcendental number theory. They are functions that appear in most proofs in this area of mathematics and that have specific, desirable properties, such as taking the value zero for many arguments, or having a zero of high...
s in Diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
and transcendental number theory
Transcendence theory
Transcendence theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.-Transcendence:...
, though for sharp results ad hoc methods in some sense inspired by the Padé theory typically replace them.
Definition
Given a function f and two integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s m ≥ 0 and n ≥ 0, the Padé approximant of order [m/n] is the rational function
which agrees with
to the highest possible order, which amounts to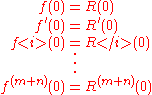.Equivalently, if
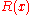is expanded in a Maclaurin series (Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
at 0), its first m + n terms would cancel the first m + n terms of
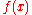, and as such:The Padé approximant is unique for given m and n, that is, the coefficients
can be uniquely determined. It is for reasons of uniqueness that the zero-th order term at the denominator of was chosen to be 1, otherwise the numerator and denominator of 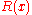would have been unique only up toUp to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
multiplication by a constant.
The Padé approximant defined above is also denoted as
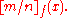
For given
, Padé approximants can be computed by WynnPeter Wynn (mathematician)
Peter Wynn is a mathematician. His main achievements concern approximation theory – in particular the theory of Padé approximants – and its application in numerical methods for improving the rate of convergence of sequences of real numbers....
's epsilon algorithm and also other sequence transformations from the partial sums
of the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of
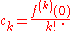
, i.e., we have can also be a formal power seriesFormal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
, and, hence, Padé approximants can also be applied to the summation of divergent series
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
.
Riemann–Padé zeta function
To study the resummation of a divergent seriesDivergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
, say
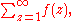
it can be useful to introduce the Padé or simply rational zeta function as
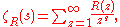
where
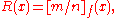
is just the Padé approximation of order (m, n) of the function f(x). The zeta regularization value at s = 0 is taken to be the sum of the divergent series.
The functional equation for this Padé zeta function is
where
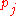and 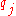are the coefficients in the Padé approximation. The subscript '0' means that the Padé is of order [0/0] and hence, we got the Riemann zeta function.DLog Padé method
Padé approximants can be used to extract critical points and exponents of functions. In thermodynamics, if a function f(x) behaves in a non-analytic way near a point x = r like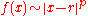, one calls x = r a critical point and p the associated critical exponent of f. If sufficient terms of the series expansion of f are known, one can approximately extract the critical points and the critical exponents from respectively the poles and residues of the Padé approximants 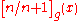where 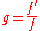.Generalizations
A Padé approximant approximates a function in one variable. An approximant in two variables is called a Chisholm approximant, in multiple variables a Canterbury approximant (after Graves-Morris at the University of Kent).External links
- Module for Padé Approximation, John H. Mathews California State University, FullertonCalifornia State University, FullertonCalifornia State University, Fullerton is a public university located in Fullerton, California. It is the largest institution in the CSU System by enrollment, it offers long-distance education and adult-degree programs...
- Padé Approximants, Oleksandr Pavlyk, The Wolfram Demonstrations Project
- A Short Introduction to Padé Approximants, Jerome Soucy Université LavalUniversité LavalLaval University is the oldest centre of education in Canada and was the first institution in North America to offer higher education in French...
- Data Analysis BriefBook: Pade Approximation, Rudolf K. Bock European Laboratory for Particle Physics, CERNCERNThe European Organization for Nuclear Research , known as CERN , is an international organization whose purpose is to operate the world's largest particle physics laboratory, which is situated in the northwest suburbs of Geneva on the Franco–Swiss border...
- Sinewave, Scott Dattalo, last accessed 2010-11-11.