
Transcendence theory
Encyclopedia
Transcendence theory is a branch of number theory
that investigates transcendental number
s, in both qualitative and quantitative ways.
tells us that if we have a non-zero polynomial
with integer coefficients then that polynomial will have a root in the complex numbers. That is, for any polynomial P with integer coefficients there will be a complex number α such that P(α) = 0. Transcendence theory is concerned with the converse question, given a complex number α, is there a polynomial P with integer coefficients such that P(α) = 0? If no such polynomial exists then the number is called transcendental.
More generally the theory deals with algebraic independence
of numbers. A set of numbers {α1,α2,…,αn} is called algebraically independent over a field k if there is no non-zero polynomial P in n variables with coefficients in k such that P(α1,α2,…,αn) = 0. So working out if a given number is transcendental is really a special case of algebraic independence where our set consists of just one number.
A related but broader notion than "algebraic" is whether there is a closed-form expression
for a number, including exponentials and logarithms as well as algebraic operations. There are various definitions of "closed-form", and questions about closed-form can often be reduced to questions about transcendence.
proved that the sine function was not an algebraic function. The question of whether certain classes of numbers could be transcendental dates back to 1748 when Euler asserted that the number logab was not algebraic for rational number
s a and b provided b is not of the form b = ac for some algebraic number c.
Euler's assertion was not proved until the twentieth century, but almost a hundred years after his claim Joseph Liouville
did manage to prove the existence of numbers that are not algebraic, something that until then had not been known for sure. His original papers on the matter in the 1840s sketched out arguments using continued fractions to construct transcendental numbers. Later, in the 1850s, he gave a necessary condition for a number to be algebraic, and thus a sufficient condition for a number to be transcendental. This transcendence criterion was not strong enough to be necessary too, and indeed it fails to detect that the number e is transcendental. But his work did provide a larger class of transcendental numbers, now known as Liouville numbers in his honour.
Liouville's criterion essentially said that algebraic numbers cannot be very well approximated by rational numbers. So if a number can be very well approximated by rational numbers then it must be transcendental. The exact meaning of "very well approximated" in Liouville's work relates to a certain exponent. He showed that if α is an algebraic number
of degree d ≥ 2 and ε is any number greater than zero, then the expression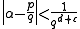
can be satisfied by only finitely many rational numbers p/q. Using this as a criterion for transcendence is not trivial, as one must check there are infinitely many solutions p/q for every d ≥ 2.
In the twentieth century work by Axel Thue
, Carl Siegel
, and Klaus Roth
reduced the exponent in Liouville's work from d + ε to d/2 + 1 + ε, and finally, in 1955, to 2 + ε. This result, known as the Thue-Siegel-Roth theorem, is ostensibly best possible, since if the exponent 2 + ε is replaced by just 2 then the result is no longer true. However, Serge Lang
conjectured an improvement of Roth's result; in particular he conjectured that q2+ε in the denominator of the right-hand side could be reduced to q2log(q)1+ε.
Roth's work effectively ended the work started by Liouville, and his theorem allowed mathematicians to prove the transcendence of many more numbers, such as the Champernowne constant
. The theorem is still not strong enough to detect all transcendental numbers, though, and many famous constants including e and π either are not or are not known to be very well approximable in the above sense.
. These are functions
which typically have many zeros at the points under consideration. Here "many zeros" may mean literally a lot of zeros, or as few as one zero but with a high multiplicity, or even many zeros all with high multiplicity. Charles Hermite
used auxiliary functions that approximated the functions ekx for each natural number
k in order to prove the transcendence of e in 1873. His work was built upon by Ferdinand von Lindemann
in the 1880s in order to prove that eα is transcendental for nonzero algebraic numbers α. In particular this proved that π is transcendental since eπi is algebraic, and thus answered the problem of antiquity as to whether it was possible to square the circle
. Karl Weierstrass
developed their work yet further and eventually proved the Lindemann-Weierstrass theorem in 1885.
In 1900 David Hilbert
posed his famous collection of problems
. The seventh of these
, and one of the hardest in Hilbert's estimation, asked about the transcendence of numbers of the form ab where a and b are algebraic, a isn't zero or one, and b is irrational. In the 1930s Alexander Gelfond
and Theodor Schneider
proved that all such numbers were indeed transcendental using a non-explicit auxiliary function whose existence was granted by Siegel's lemma
. This result, the Gelfond–Schneider theorem
, proved the transcendence of numbers such as eπ
and the Gelfond–Schneider constant.
The next big result in this field occurred in the 1960s, when Alan Baker made progress on a problem posed by Gel'fond on linear forms in logarithms
. Gel'fond himself had managed to find a non-trivial lower bound for the quantity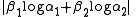
where all four unknowns are algebraic, the αs being neither zero nor one and the βs being irrational. Finding similar lower bounds for the sum of three or more logarithms had eluded Gel'fond, though. The proof of Baker's theorem
contained such bounds, solving Gauss' class number problem for class number one in the process. This work won Baker the Fields medal
for its uses in solving Diophantine equation
s. From a purely transcendental number theoretic viewpoint, Baker had proved that if α1,...,αn are algebraic numbers, none of them zero or one, and β1,...,βn are algebraic numbers such that 1,β1,...,βn are linearly independent over the rational numbers, then the number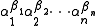
is transcendental.
started to develop set theory
and in 1874 published a paper proving
that the algebraic numbers could be put in one-to-one correspondence
with the set of natural numbers, and thus that the set of transcendental numbers must be uncountable
. Later, in 1891, Cantor used his more familiar diagonal argument
to prove the same result. While Cantor's result is often quoted as being purely existential and thus unusable for constructing a single transcendental number, the proofs in both the aforementioned papers give methods to construct transcendental numbers.
While Cantor used set theory to prove the plenitude of transcendental numbers, a recent development has been the use of model theory
in attempts to prove an unsolved problem in transcendental number theory. The problem is to determine the transcendence degree
of the field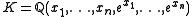
for complex numbers x1,...,xn that are linearly independent over the rational numbers. Stephen Schanuel
conjectured
that the answer is n, but no proof is known. In 2004, though, Boris Zilber published a paper that used model theoretic techniques to create a structure that behaves very much like the complex numbers equipped with the operations of addition, multiplication, and exponentiation. Moreover, in this abstract structure Schanuel's conjecture does indeed hold. Unfortunately it is not yet known that this structure is in fact the same as the complex numbers with the operations mentioned, it could be that Schanuel's conjecture is false and that there exists some other abstract structure that behaves very similarly to the complex numbers but where Schanuel's conjecture holds. Zilber did provide several criteria that would prove the structure in question was C, but could not prove the so-called Strong Exponential Closure axiom. The simplest case of this axiom has since been proved, but a proof that it holds in full generality is required to complete the proof of the conjecture.
used a cardinality argument to show that there are only countably many algebraic numbers, and hence almost all
numbers are transcendental. Transcendental numbers therefore represent the typical case; even so, it may be extremely difficult to prove that a given number is transcendental (or even simply irrational).
For this reason transcendence theory often works towards a more quantitative approach. So given a particular complex number α one can ask how close α is to being an algebraic number. For example, if one supposes that the number α is algebraic then can one show that it must have very high degree or a minimum polynomial with very large coefficients? Ultimately if it is possible to show that no finite degree or size of coefficient is sufficient then the number must be transcendental. Since a number α is transcendental if and only if P(α)≠0 for every non-zero polynomial P with integer coefficents, this problem can be approached by trying to find lower bounds of the form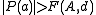
where the right hand side is some positive function depending on some measure A of the size of the coefficient
s of P, and its degree
d, and such that these lower bounds apply to all P ≠ 0. Such a bound is called a transcendence measure.
The case of d = 1 is that of "classical" diophantine approximation
asking for lower bounds for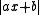 .
.
The methods of transcendence theory and diophantine approximation have much in common: they both use the auxiliary function
concept.
was the major advance in transcendence theory in the period 1900-1950. In the 1960s the method of Alan Baker on linear forms in logarithms
of algebraic number
s reanimated transcendence theory, with applications to numerous classical problems and diophantine equation
s.
A major problem in transcendence theory is showing that a particular set of numbers is algebraically independent rather than just showing that individual elements are transcendental. So while we know that e and π are transcendental that doesn't imply that e + π is transcendental, nor other combinations of the two (except eπ, Gelfond's constant
, which is known to be transcendental). Another major problem is dealing with numbers that are not related to the exponential function. The main results in transcendence theory tend to revolve around e and the logarithm function, which means that wholly new methods tend to be required to deal with numbers that cannot be expressed in terms of these two objects in an elementary fashion.
Schanuel's conjecture
would solve the first of these problems somewhat as it deals with algebraic independence and would indeed confirm that e+π is transcendental. It still revolves around the exponential function however and so would not necessarily deal with numbers such as Apéry's constant
or the Euler–Mascheroni constant
. Another extremely difficult unsolved problem is the so-called Constant or Identity problem
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
that investigates transcendental number
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
s, in both qualitative and quantitative ways.
Transcendence
The fundamental theorem of algebraFundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
tells us that if we have a non-zero polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with integer coefficients then that polynomial will have a root in the complex numbers. That is, for any polynomial P with integer coefficients there will be a complex number α such that P(α) = 0. Transcendence theory is concerned with the converse question, given a complex number α, is there a polynomial P with integer coefficients such that P(α) = 0? If no such polynomial exists then the number is called transcendental.
More generally the theory deals with algebraic independence
Algebraic independence
In abstract algebra, a subset S of a field L is algebraically independent over a subfield K if the elements of S do not satisfy any non-trivial polynomial equation with coefficients in K...
of numbers. A set of numbers {α1,α2,…,αn} is called algebraically independent over a field k if there is no non-zero polynomial P in n variables with coefficients in k such that P(α1,α2,…,αn) = 0. So working out if a given number is transcendental is really a special case of algebraic independence where our set consists of just one number.
A related but broader notion than "algebraic" is whether there is a closed-form expression
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
for a number, including exponentials and logarithms as well as algebraic operations. There are various definitions of "closed-form", and questions about closed-form can often be reduced to questions about transcendence.
Approximation by rational numbers: Liouville to Roth
Use of the term transcendental to refer to an object that is not algebraic dates back to the seventeenth century, when Gottfried LeibnizGottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
proved that the sine function was not an algebraic function. The question of whether certain classes of numbers could be transcendental dates back to 1748 when Euler asserted that the number logab was not algebraic for rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s a and b provided b is not of the form b = ac for some algebraic number c.
Euler's assertion was not proved until the twentieth century, but almost a hundred years after his claim Joseph Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
did manage to prove the existence of numbers that are not algebraic, something that until then had not been known for sure. His original papers on the matter in the 1840s sketched out arguments using continued fractions to construct transcendental numbers. Later, in the 1850s, he gave a necessary condition for a number to be algebraic, and thus a sufficient condition for a number to be transcendental. This transcendence criterion was not strong enough to be necessary too, and indeed it fails to detect that the number e is transcendental. But his work did provide a larger class of transcendental numbers, now known as Liouville numbers in his honour.
Liouville's criterion essentially said that algebraic numbers cannot be very well approximated by rational numbers. So if a number can be very well approximated by rational numbers then it must be transcendental. The exact meaning of "very well approximated" in Liouville's work relates to a certain exponent. He showed that if α is an algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
of degree d ≥ 2 and ε is any number greater than zero, then the expression
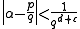
can be satisfied by only finitely many rational numbers p/q. Using this as a criterion for transcendence is not trivial, as one must check there are infinitely many solutions p/q for every d ≥ 2.
In the twentieth century work by Axel Thue
Axel Thue
Axel Thue was a Norwegian mathematician, known for highly original work in diophantine approximation, and combinatorics....
, Carl Siegel
Carl Ludwig Siegel
Carl Ludwig Siegel was a mathematician specialising in number theory and celestial mechanics. He was one of the most important mathematicians of the 20th century.-Biography:...
, and Klaus Roth
Klaus Roth
Klaus Friedrich Roth is a British mathematician known for work on diophantine approximation, the large sieve, and irregularities of distribution. He was born in Breslau, Prussia, but raised and educated in the UK. He graduated from Peterhouse, Cambridge in 1945...
reduced the exponent in Liouville's work from d + ε to d/2 + 1 + ε, and finally, in 1955, to 2 + ε. This result, known as the Thue-Siegel-Roth theorem, is ostensibly best possible, since if the exponent 2 + ε is replaced by just 2 then the result is no longer true. However, Serge Lang
Serge Lang
Serge Lang was a French-born American mathematician. He was known for his work in number theory and for his mathematics textbooks, including the influential Algebra...
conjectured an improvement of Roth's result; in particular he conjectured that q2+ε in the denominator of the right-hand side could be reduced to q2log(q)1+ε.
Roth's work effectively ended the work started by Liouville, and his theorem allowed mathematicians to prove the transcendence of many more numbers, such as the Champernowne constant
Champernowne constant
In mathematics, the Champernowne constant C10 is a transcendental real constant whose decimal expansion has important properties. It is named after mathematician D. G...
. The theorem is still not strong enough to detect all transcendental numbers, though, and many famous constants including e and π either are not or are not known to be very well approximable in the above sense.
Auxiliary functions: Hermite to Baker
Fortunately other methods were pioneered in the nineteenth century to deal with the algebraic properties of e, and consequently of π through Euler's identity. This work centred on use of the so-called auxiliary functionAuxiliary function
In mathematics, auxiliary functions are an important construction in transcendental number theory. They are functions that appear in most proofs in this area of mathematics and that have specific, desirable properties, such as taking the value zero for many arguments, or having a zero of high...
. These are functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
which typically have many zeros at the points under consideration. Here "many zeros" may mean literally a lot of zeros, or as few as one zero but with a high multiplicity, or even many zeros all with high multiplicity. Charles Hermite
Charles Hermite
Charles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....
used auxiliary functions that approximated the functions ekx for each natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
k in order to prove the transcendence of e in 1873. His work was built upon by Ferdinand von Lindemann
Ferdinand von Lindemann
Carl Louis Ferdinand von Lindemann was a German mathematician, noted for his proof, published in 1882, that π is a transcendental number, i.e., it is not a root of any polynomial with rational coefficients....
in the 1880s in order to prove that eα is transcendental for nonzero algebraic numbers α. In particular this proved that π is transcendental since eπi is algebraic, and thus answered the problem of antiquity as to whether it was possible to square the circle
Squaring the circle
Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
. Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
developed their work yet further and eventually proved the Lindemann-Weierstrass theorem in 1885.
In 1900 David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
posed his famous collection of problems
Hilbert's problems
Hilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
. The seventh of these
Hilbert's seventh problem
Hilbert's seventh problem is one of David Hilbert's list of open mathematical problems posed in 1900. It concerns the irrationality and transcendence of certain numbers...
, and one of the hardest in Hilbert's estimation, asked about the transcendence of numbers of the form ab where a and b are algebraic, a isn't zero or one, and b is irrational. In the 1930s Alexander Gelfond
Alexander Gelfond
Alexander Osipovich Gelfond was a Soviet mathematician, author of Gelfond's theorem.-Biography:Alexander Gelfond was born in St Petersburg, Russian Empire in the family of a professional physician and amateur philosopher Osip Isaakovich Gelfond. He entered the Moscow State University in 1924,...
and Theodor Schneider
Theodor Schneider
Theodor Schneider was a German mathematician, best known for providing proof of what is now known as the Gelfond–Schneider theorem in 1935....
proved that all such numbers were indeed transcendental using a non-explicit auxiliary function whose existence was granted by Siegel's lemma
Siegel's lemma
In transcendental number theory and Diophantine approximation, Siegel's lemma refers to bounds on the solutions of linear equations obtained by the construction of auxiliary functions. The existence of these polynomials was proven by Axel Thue; Thue's proof used Dirichlet's box principle. Carl...
. This result, the Gelfond–Schneider theorem
Gelfond–Schneider theorem
In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider...
, proved the transcendence of numbers such as eπ
Gelfond's constant
In mathematics, Gelfond's constant, named after Aleksandr Gelfond, is eπ, that is, e to the power of π. Like both e and π, this constant is a transcendental number. This can be proven by the Gelfond–Schneider theorem and noting the fact that...
and the Gelfond–Schneider constant.
The next big result in this field occurred in the 1960s, when Alan Baker made progress on a problem posed by Gel'fond on linear forms in logarithms
Linear forms in logarithms
In number theory the method of linear forms in logarithms is the application of estimatesfor the magnitude of a finite sum\sum \beta_i\log\alpha_i=\Lambda,...
. Gel'fond himself had managed to find a non-trivial lower bound for the quantity
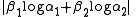
where all four unknowns are algebraic, the αs being neither zero nor one and the βs being irrational. Finding similar lower bounds for the sum of three or more logarithms had eluded Gel'fond, though. The proof of Baker's theorem
Baker's theorem
In transcendence theory, a mathematical discipline, Baker's theorem gives a lower bound for linear combinations of logarithms of algebraic numbers...
contained such bounds, solving Gauss' class number problem for class number one in the process. This work won Baker the Fields medal
Fields Medal
The Fields Medal, officially known as International Medal for Outstanding Discoveries in Mathematics, is a prize awarded to two, three, or four mathematicians not over 40 years of age at each International Congress of the International Mathematical Union , a meeting that takes place every four...
for its uses in solving Diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
s. From a purely transcendental number theoretic viewpoint, Baker had proved that if α1,...,αn are algebraic numbers, none of them zero or one, and β1,...,βn are algebraic numbers such that 1,β1,...,βn are linearly independent over the rational numbers, then the number
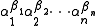
is transcendental.
Other techniques: Cantor and Zilber
In the 1870s Georg CantorGeorg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
started to develop set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
and in 1874 published a paper proving
Cantor's first uncountability proof
Georg Cantor's first uncountability proof demonstrates that the set of all real numbers is uncountable. This proof differs from the more familiar proof that uses his diagonal argument...
that the algebraic numbers could be put in one-to-one correspondence
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
with the set of natural numbers, and thus that the set of transcendental numbers must be uncountable
Uncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
. Later, in 1891, Cantor used his more familiar diagonal argument
Cantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
to prove the same result. While Cantor's result is often quoted as being purely existential and thus unusable for constructing a single transcendental number, the proofs in both the aforementioned papers give methods to construct transcendental numbers.
While Cantor used set theory to prove the plenitude of transcendental numbers, a recent development has been the use of model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
in attempts to prove an unsolved problem in transcendental number theory. The problem is to determine the transcendence degree
Transcendence degree
In abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
of the field
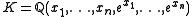
for complex numbers x1,...,xn that are linearly independent over the rational numbers. Stephen Schanuel
Stephen Schanuel
Stephen H. Schanuel is an American mathematician working in the fields of abstract algebra and number theory, more specifically category theory and measure theory....
conjectured
Schanuel's conjecture
In mathematics, specifically transcendence theory, Schanuel's conjecture is a conjecture made by Stephen Schanuel in the 1960s concerning the transcendence degree of certain field extensions of the rational numbers.-Statement:The conjecture is as follows:...
that the answer is n, but no proof is known. In 2004, though, Boris Zilber published a paper that used model theoretic techniques to create a structure that behaves very much like the complex numbers equipped with the operations of addition, multiplication, and exponentiation. Moreover, in this abstract structure Schanuel's conjecture does indeed hold. Unfortunately it is not yet known that this structure is in fact the same as the complex numbers with the operations mentioned, it could be that Schanuel's conjecture is false and that there exists some other abstract structure that behaves very similarly to the complex numbers but where Schanuel's conjecture holds. Zilber did provide several criteria that would prove the structure in question was C, but could not prove the so-called Strong Exponential Closure axiom. The simplest case of this axiom has since been proved, but a proof that it holds in full generality is required to complete the proof of the conjecture.
Approaches
A typical problem in this area of mathematics is to work out whether a given number is transcendental. CantorGeorg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
used a cardinality argument to show that there are only countably many algebraic numbers, and hence almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
numbers are transcendental. Transcendental numbers therefore represent the typical case; even so, it may be extremely difficult to prove that a given number is transcendental (or even simply irrational).
For this reason transcendence theory often works towards a more quantitative approach. So given a particular complex number α one can ask how close α is to being an algebraic number. For example, if one supposes that the number α is algebraic then can one show that it must have very high degree or a minimum polynomial with very large coefficients? Ultimately if it is possible to show that no finite degree or size of coefficient is sufficient then the number must be transcendental. Since a number α is transcendental if and only if P(α)≠0 for every non-zero polynomial P with integer coefficents, this problem can be approached by trying to find lower bounds of the form
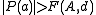
where the right hand side is some positive function depending on some measure A of the size of the coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s of P, and its degree
Degree (mathematics)
In mathematics, there are several meanings of degree depending on the subject.- Unit of angle :A degree , usually denoted by ° , is a measurement of a plane angle, representing 1⁄360 of a turn...
d, and such that these lower bounds apply to all P ≠ 0. Such a bound is called a transcendence measure.
The case of d = 1 is that of "classical" diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
asking for lower bounds for
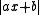 .
.The methods of transcendence theory and diophantine approximation have much in common: they both use the auxiliary function
Auxiliary function
In mathematics, auxiliary functions are an important construction in transcendental number theory. They are functions that appear in most proofs in this area of mathematics and that have specific, desirable properties, such as taking the value zero for many arguments, or having a zero of high...
concept.
Major results
The Gelfond–Schneider theoremGelfond–Schneider theorem
In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider...
was the major advance in transcendence theory in the period 1900-1950. In the 1960s the method of Alan Baker on linear forms in logarithms
Linear forms in logarithms
In number theory the method of linear forms in logarithms is the application of estimatesfor the magnitude of a finite sum\sum \beta_i\log\alpha_i=\Lambda,...
of algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s reanimated transcendence theory, with applications to numerous classical problems and diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
s.
Open problems
While the Gelfond-Schneider theorem proved that a large class of numbers was transcendental, this class was still countable. Many well known mathematical constants are still not known to be transcendental, and in some cases it is not even known whether they are rational or irrational. A partial list can be found here.A major problem in transcendence theory is showing that a particular set of numbers is algebraically independent rather than just showing that individual elements are transcendental. So while we know that e and π are transcendental that doesn't imply that e + π is transcendental, nor other combinations of the two (except eπ, Gelfond's constant
Gelfond's constant
In mathematics, Gelfond's constant, named after Aleksandr Gelfond, is eπ, that is, e to the power of π. Like both e and π, this constant is a transcendental number. This can be proven by the Gelfond–Schneider theorem and noting the fact that...
, which is known to be transcendental). Another major problem is dealing with numbers that are not related to the exponential function. The main results in transcendence theory tend to revolve around e and the logarithm function, which means that wholly new methods tend to be required to deal with numbers that cannot be expressed in terms of these two objects in an elementary fashion.
Schanuel's conjecture
Schanuel's conjecture
In mathematics, specifically transcendence theory, Schanuel's conjecture is a conjecture made by Stephen Schanuel in the 1960s concerning the transcendence degree of certain field extensions of the rational numbers.-Statement:The conjecture is as follows:...
would solve the first of these problems somewhat as it deals with algebraic independence and would indeed confirm that e+π is transcendental. It still revolves around the exponential function however and so would not necessarily deal with numbers such as Apéry's constant
Apéry's constant
In mathematics, Apéry's constant is a number that occurs in a variety of situations. It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics...
or the Euler–Mascheroni constant
Euler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
. Another extremely difficult unsolved problem is the so-called Constant or Identity problem
Constant problem
In mathematics, the constant problem is the problem of deciding if a given expression is equal to zero.-The problem:This problem is also referred to as the identity problem or the method of zero estimates. It has no formal statement as such but refers to a general problem prevalent in...
.

