
Algebraic independence
Encyclopedia
In abstract algebra
, a subset
S of a field
L is algebraically independent over a subfield
K if the elements of S do not satisfy any non-trivial
polynomial
equation with coefficients in K. This means that for every finite sequence α1, ..., αn of elements of S, no two of which are the same, then if P has coefficients in K and
then P is the zero polynomial.
In particular, a one element set {α} is algebraically independent over K if and only if
α is transcendental over K. In general, all the elements of an algebraically independent set over K are by necessity transcendental over K, but that is far from being a sufficient condition.
For example, the subset {√π
, 2π+1} of the real number
s R is not algebraically independent over the rational number
s Q, since the non-zero polynomial
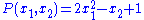
yields zero when √π is substituted for x1 and 2π+1 is substituted for x2.
The Lindemann-Weierstrass theorem can often be used to prove that some sets are algebraically independent over Q. It states that whenever α1,...,αn are algebraic number
s that are linearly independent over Q, then eα1,...,eαn are algebraically independent over Q.
It is not known whether the set {π
, e
} is algebraically independent over Q. In fact, it is not even known if π+e is irrational.
Nesterenko
proved in 1996 that:
Given a field extension
L/K, we can use Zorn's lemma
to show that there always exists a maximal algebraically independent subset of L over K. Further, all the maximal algebraically independent subsets have the same cardinality, known as the transcendence degree
of the extension.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
S of a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
L is algebraically independent over a subfield
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K if the elements of S do not satisfy any non-trivial
Trivial (mathematics)
In mathematics, the adjective trivial is frequently used for objects that have a very simple structure...
polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
equation with coefficients in K. This means that for every finite sequence α1, ..., αn of elements of S, no two of which are the same, then if P has coefficients in K and
- P(α1,...,αn) = 0
then P is the zero polynomial.
In particular, a one element set {α} is algebraically independent over K if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
α is transcendental over K. In general, all the elements of an algebraically independent set over K are by necessity transcendental over K, but that is far from being a sufficient condition.
For example, the subset {√π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, 2π+1} of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R is not algebraically independent over the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q, since the non-zero polynomial
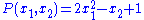
yields zero when √π is substituted for x1 and 2π+1 is substituted for x2.
The Lindemann-Weierstrass theorem can often be used to prove that some sets are algebraically independent over Q. It states that whenever α1,...,αn are algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s that are linearly independent over Q, then eα1,...,eαn are algebraically independent over Q.
It is not known whether the set {π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
} is algebraically independent over Q. In fact, it is not even known if π+e is irrational.
Nesterenko
Yuri Valentinovich Nesterenko
Yuri Valentinovich Nesterenko is a mathematician who has written papers in algebraic independence theory and transcendental number theory.In 1997 he was awarded the Ostrowski Prize for his proof that the numbers π and eπ are algebraically independent...
proved in 1996 that:
- the numbers π, eπ, and ΓGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
(1/4) are algebraically independent over Q. - the numbers π, eπ√3, and Γ(1/3) are algebraically independent over Q.
- for all positive integers n, the numbers π, eπ√n are algebraically independent over Q.
Given a field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
L/K, we can use Zorn's lemma
Zorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
to show that there always exists a maximal algebraically independent subset of L over K. Further, all the maximal algebraically independent subsets have the same cardinality, known as the transcendence degree
Transcendence degree
In abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
of the extension.

