
SABR Volatility Model
Encyclopedia
In mathematical finance
, the SABR model is a stochastic volatility
model, which attempts to capture the volatility smile
in derivatives markets. The name stands for "Stochastic
Alpha
, Beta
, Rho
", referring to the parameters of the model. The SABR model is widely used by practitioners in the financial industry, especially in the interest rate derivatives
markets. It was developed by Patrick Hagan, Deep Kumar, Andrew Lesniewski, and Diana Woodward.
 , such as a LIBOR forward rate
, such as a LIBOR forward rate
, a forward swap rate, or a forward stock price. The volatility of the forward is described by a parameter
is described by a parameter  . SABR is a dynamic model in which both
. SABR is a dynamic model in which both  and
and  are represented by stochastic state variables whose time evolution is given by the following system of stochastic differential equations:
are represented by stochastic state variables whose time evolution is given by the following system of stochastic differential equations:
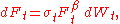
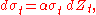
with the prescribed time zero (currently observed) values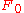 and
and 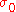 . Here,
. Here,  and
and 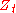 are two correlated Wiener processes
are two correlated Wiener processes
with correlation coefficient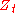 . The constant parameters
. The constant parameters 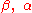 satisfy the conditions
satisfy the conditions  .
.
The above dynamics is a stochastic version of the CEV model with the skewness parameter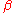 : in fact, it reduces to the CEV model if
: in fact, it reduces to the CEV model if  The parameter
The parameter  is often referred to as the volvol, and its meaning is that of the lognormal volatility of the volatility parameter
is often referred to as the volvol, and its meaning is that of the lognormal volatility of the volatility parameter  .
.
 struck at
struck at  , which expires
, which expires  years from now. The value of this option is equal to the suitably discounted expected value of the payoff
years from now. The value of this option is equal to the suitably discounted expected value of the payoff  under the probability distribution of the process
under the probability distribution of the process  .
.
Except for the special cases of and
and  , no closed form expression for this probability distribution is known. The general case can be solved approximately by means of an asymptotic expansion in the parameter
, no closed form expression for this probability distribution is known. The general case can be solved approximately by means of an asymptotic expansion in the parameter  . Under typical market conditions, this parameter is small and the approximate solution is actually quite accurate. Also significantly, this solution has a rather simple functional form, is very easy to implement in computer code, and lends itself well to risk management of large portfolios of options in real time.
. Under typical market conditions, this parameter is small and the approximate solution is actually quite accurate. Also significantly, this solution has a rather simple functional form, is very easy to implement in computer code, and lends itself well to risk management of large portfolios of options in real time.
It is convenient to express the solution in terms of the implied volatility
of the option. Namely, we force the SABR model price of the option into the form of the Black model
valuation formula. Then the implied volatility, which is the value of the lognormal volatility parameter in Black's model that forces it to match the SABR price, is approximately given by:

where, for clarity, we have set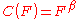 . The value
. The value  denotes a conveniently chosen midpoint between
denotes a conveniently chosen midpoint between  and
and  (such as the geometric average
(such as the geometric average  or the arithmetic average
or the arithmetic average 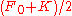 ). We have also set
). We have also set
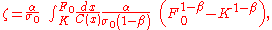
and
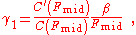

The function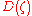 entering the formula above is given by
entering the formula above is given by
Mathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
, the SABR model is a stochastic volatility
Stochastic volatility
Stochastic volatility models are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the...
model, which attempts to capture the volatility smile
Volatility Smile
In finance, the volatility smile is a long-observed pattern in which at-the-money options tend to have lower implied volatilities than in- or out-of-the-money options. The pattern displays different characteristics for different markets and results from the probability of extreme moves...
in derivatives markets. The name stands for "Stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
Alpha
Alpha
Alpha is the first letter of the Greek alphabet. Alpha or ALPHA may also refer to:-Science:*Alpha , the highest ranking individuals in a community of social animals...
, Beta
Beta
Beta is the second letter of the Greek alphabet. Beta or BETA may also refer to:-Biology:*Beta , a genus of flowering plants, mostly referred to as beets*Beta, a rank in a community of social animals...
, Rho
Rho
Rho is the 17th letter of the Greek alphabet. In the system of Greek numerals, it has a value of 100. It is derived from Semitic resh "head"...
", referring to the parameters of the model. The SABR model is widely used by practitioners in the financial industry, especially in the interest rate derivatives
Interest rate derivative
An interest rate derivative is a derivative where the underlying asset is the right to pay or receive a notional amount of money at a given interest rate...
markets. It was developed by Patrick Hagan, Deep Kumar, Andrew Lesniewski, and Diana Woodward.
Dynamics
The SABR model describes a single forward , such as a LIBOR forward rate
, such as a LIBOR forward rateForward rate
The forward rate is the future yield on a bond. It is calculated using the yield curve. For example, the yield on a three-month Treasury bill six months from now is a forward rate.-Forward rate calculation:...
, a forward swap rate, or a forward stock price. The volatility of the forward
 is described by a parameter
is described by a parameter  . SABR is a dynamic model in which both
. SABR is a dynamic model in which both  and
and  are represented by stochastic state variables whose time evolution is given by the following system of stochastic differential equations:
are represented by stochastic state variables whose time evolution is given by the following system of stochastic differential equations: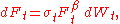
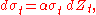
with the prescribed time zero (currently observed) values
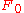 and
and 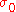 . Here,
. Here,  and
and 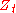 are two correlated Wiener processes
are two correlated Wiener processesWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
with correlation coefficient
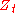 . The constant parameters
. The constant parameters 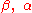 satisfy the conditions
satisfy the conditions  .
.The above dynamics is a stochastic version of the CEV model with the skewness parameter
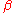 : in fact, it reduces to the CEV model if
: in fact, it reduces to the CEV model if  The parameter
The parameter  is often referred to as the volvol, and its meaning is that of the lognormal volatility of the volatility parameter
is often referred to as the volvol, and its meaning is that of the lognormal volatility of the volatility parameter  .
.Asymptotic solution
We consider a European option (say, a call) on the forward struck at
struck at  , which expires
, which expires  years from now. The value of this option is equal to the suitably discounted expected value of the payoff
years from now. The value of this option is equal to the suitably discounted expected value of the payoff  under the probability distribution of the process
under the probability distribution of the process  .
.Except for the special cases of
 and
and  , no closed form expression for this probability distribution is known. The general case can be solved approximately by means of an asymptotic expansion in the parameter
, no closed form expression for this probability distribution is known. The general case can be solved approximately by means of an asymptotic expansion in the parameter  . Under typical market conditions, this parameter is small and the approximate solution is actually quite accurate. Also significantly, this solution has a rather simple functional form, is very easy to implement in computer code, and lends itself well to risk management of large portfolios of options in real time.
. Under typical market conditions, this parameter is small and the approximate solution is actually quite accurate. Also significantly, this solution has a rather simple functional form, is very easy to implement in computer code, and lends itself well to risk management of large portfolios of options in real time.It is convenient to express the solution in terms of the implied volatility
Implied volatility
In financial mathematics, the implied volatility of an option contract is the volatility of the price of the underlying security that is implied by the market price of the option based on an option pricing model. In other words, it is the volatility that, when used in a particular pricing model,...
of the option. Namely, we force the SABR model price of the option into the form of the Black model
Black model
The Black model is a variant of the Black–Scholes option pricing model. Its primary applications are for pricing bond options, interest rate caps / floors, and swaptions...
valuation formula. Then the implied volatility, which is the value of the lognormal volatility parameter in Black's model that forces it to match the SABR price, is approximately given by:

where, for clarity, we have set
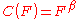 . The value
. The value  denotes a conveniently chosen midpoint between
denotes a conveniently chosen midpoint between  and
and  (such as the geometric average
(such as the geometric average  or the arithmetic average
or the arithmetic average 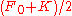 ). We have also set
). We have also set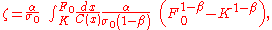
and
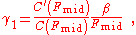

The function
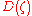 entering the formula above is given by
entering the formula above is given by-

Alternatively, one can express the SABR price in terms of the normal Black's model. Then the implied normal volatility can be asymptotically computed by means of the following expression:

It is worth noting that the normal SABR implied volatility is generally somewhat more accurate than the lognormal implied volatility.

