Black model
Encyclopedia
The Black model is a variant of the Black–Scholes option pricing model. Its primary applications are for pricing bond option
s, interest rate caps / floors, and swaption
s. It was first presented in a paper written by Fischer Black
in 1976.
Black's model can be generalized into a class of models known as log-normal forward models, also referred to as LIBOR market model
.
of the underlying is replaced by a discounted futures price F.
Suppose there is constant risk-free interest rate r and the futures price F(t) of a particular underlying is log-normal with constant volatility σ. Then the Black formula states the price for a European call option of maturity T on a futures contract
with futures price K and delivery date T (with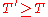
) is
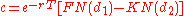
The corresponding put price is
where
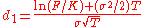
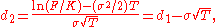
and N(.) is the cumulative normal distribution function.
Note that T' doesn't appear in the formulae even though it could be greater than T. This is because futures contracts are marked to market and so the payoff is realized when the option is exercised. If we consider an option on a forward contract
expiring at time T' > T, the payoff doesn't occur until T' . Thus the discount factor
is replaced by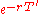 
since one must take into account the time value of money. The difference in the two cases is clear from the derivation below.
, which in turn is a simple, but clever, application of the Black–Scholes formula.
The payoff of the call option on the futures contract is max (0, F(T) - K). We can consider this an exchange (Margrabe) option by considering the first asset to be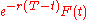
and the second asset to be the riskless bond paying off $1 at time T. Then the call option is exercised at time T when the first asset is worth more than K riskless bonds. The assumptions of Margrabe's formula are satisfied with these assets.
The only remaining thing to check is that the first asset is indeed an asset. This can be seen by considering a portfolio formed at time 0 by going long a forward contract with delivery date T and short F(0) riskless bonds (note that under the deterministic interest rate, the forward and futures prices are equal so there is no ambiguity here). Then at any time t you can unwind your obligation for the forward contract by shorting another forward with the same delivery date to get the difference in forward prices, but discounted to present value:
. Liquidating the F(0) riskless bonds, each of which is worth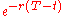 
, results in a net payoff of 
.
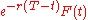Online tools
Bond option
In finance, a bond option is an option to buy or sell a bond at a certain price on or before the option expiry date. These instruments are typically traded OTC....
s, interest rate caps / floors, and swaption
Swaption
A swaption is an option granting its owner the right but not the obligation to enter into an underlying swap. Although options can be traded on a variety of swaps, the term "swaption" typically refers to options on interest rate swaps....
s. It was first presented in a paper written by Fischer Black
Fischer Black
Fischer Sheffey Black was an American economist, best known as one of the authors of the famous Black–Scholes equation.-Background:...
in 1976.
Black's model can be generalized into a class of models known as log-normal forward models, also referred to as LIBOR market model
LIBOR Market Model
The LIBOR market model, also known as the BGM Model , is a financial model of interest rates...
.
The Black formula
The Black formula is similar to the Black–Scholes formula for valuing stock options except that the spot priceSpot price
The spot price or spot rate of a commodity, a security or a currency is the price that is quoted for immediate settlement . Spot settlement is normally one or two business days from trade date...
of the underlying is replaced by a discounted futures price F.
Suppose there is constant risk-free interest rate r and the futures price F(t) of a particular underlying is log-normal with constant volatility σ. Then the Black formula states the price for a European call option of maturity T on a futures contract
Futures contract
In finance, a futures contract is a standardized contract between two parties to exchange a specified asset of standardized quantity and quality for a price agreed today with delivery occurring at a specified future date, the delivery date. The contracts are traded on a futures exchange...
with futures price K and delivery date T (with
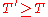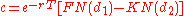
) isThe corresponding put price is
where
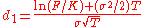
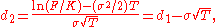
and N(.) is the cumulative normal distribution function.
Note that T' doesn't appear in the formulae even though it could be greater than T. This is because futures contracts are marked to market and so the payoff is realized when the option is exercised. If we consider an option on a forward contract
Forward contract
In finance, a forward contract or simply a forward is a non-standardized contract between two parties to buy or sell an asset at a specified future time at a price agreed today. This is in contrast to a spot contract, which is an agreement to buy or sell an asset today. It costs nothing to enter a...
expiring at time T' > T, the payoff doesn't occur until T' . Thus the discount factor
is replaced by 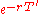since one must take into account the time value of money. The difference in the two cases is clear from the derivation below.Derivation and assumptions
The Black formula is easily derived from use of Margrabe's formulaMargrabe's formula
In mathematical finance, Margrabe's formula is an option pricing formula. It applies to an option to exchange one risky asset for another risky asset at maturity....
, which in turn is a simple, but clever, application of the Black–Scholes formula.
The payoff of the call option on the futures contract is max (0, F(T) - K). We can consider this an exchange (Margrabe) option by considering the first asset to be
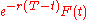and the second asset to be the riskless bond paying off $1 at time T. Then the call option is exercised at time T when the first asset is worth more than K riskless bonds. The assumptions of Margrabe's formula are satisfied with these assets.The only remaining thing to check is that the first asset is indeed an asset. This can be seen by considering a portfolio formed at time 0 by going long a forward contract with delivery date T and short F(0) riskless bonds (note that under the deterministic interest rate, the forward and futures prices are equal so there is no ambiguity here). Then at any time t you can unwind your obligation for the forward contract by shorting another forward with the same delivery date to get the difference in forward prices, but discounted to present value:
. Liquidating the F(0) riskless bonds, each of which is worth 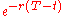, results in a net payoff of 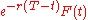.External links
Discussion- Martingales and Measures: Black's Model Dr. Jacqueline Henn-Overbeck, University of BaselUniversity of BaselThe University of Basel is located in Basel, Switzerland, and is considered to be one of leading universities in the country...
- Bond Options, Caps and the Black Model Dr. Milica Cudina, University of Texas at AustinUniversity of Texas at AustinThe University of Texas at Austin is a state research university located in Austin, Texas, USA, and is the flagship institution of the The University of Texas System. Founded in 1883, its campus is located approximately from the Texas State Capitol in Austin...
Online tools
- Caplet And Floorlet Calculator Dr. Shing Hing Man, Thomson-Reuters' Risk Management
- 'Greeks' Calculator using the Black model, Razvan Pascalau, Univ. of Alabama