Fat tail
Encyclopedia
A fat-tailed distribution is a probability distribution
that has the property, along with the heavy-tailed distribution
s, that they exhibit extremely large skewness
or kurtosis
. This comparison is often made relative to the ubiquitous normal distribution, which itself is an example of an exceptionally thin tail distribution, or to the exponential distribution
. Fat tail distributions have been empirically encountered in a fair number of areas: economics, physics, and earth sciences. Fat tail distributions have power law
decay in the tail of the distribution, but do not necessarily follow a power law everywhere.
X is said to have a fat tail if
That is, if X has a probability density function
,
,
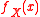Here the notation "
" is the "twiddles" notation used for the asymptotic equivalence of functions. Some reserve the term "fat tail" for distributions only where 0 < α < 2 (i.e. only in cases with infinite variance).
by five or more standard deviation
s ("5-sigma event") are extremely rare, with 10- or more sigma being practically impossible. On the other hand, fat tail distributions such as the Cauchy distribution
(and all other stable distributions with the exception of the normal distribution) are examples of fat tail distributions that have "infinite sigma" (more technically: "the variance
does not exist").
Thus when data naturally arise from a fat tail distribution, shoehorning the normal distribution model of risk—and an estimate of the corresponding sigma based necessarily on a finite sample size—would severely understate the true risk. Many—notably Benoît Mandelbrot
as well as Nassim Taleb
—have noted this shortcoming of the normal distribution model and have proposed that fat tail distributions such as the stable distribution govern asset returns frequently found in finance
.
The Black–Scholes model of option pricing is based on a normal distribution. If the distribution is actually a fat-tailed one, then the model will under-price options
that are far out of the money
, since a 5 or 7 sigma event is much more likely than the normal distribution would predict.
, fat tails are considered undesirable because of the additional risk
they imply. For example, an investment strategy may have an expected return, after one year, that is five times its standard deviation. Assuming a normal distribution, the likelihood of its failure (negative return) is less than one in a million; in practice, it may be higher. Normal distributions that emerge in finance generally do so because the factors influencing an asset's value or price are mathematically "well-behaved", and the central limit theorem
provides for such a distribution. However, traumatic "real-world" events (such as an oil shock, a large corporate bankruptcy, or an abrupt change in a political situation) are usually not mathematically well-behaved
.
Historical examples include the Black Monday (1987)
, or the unpegging of some currencies.
Fat tails in market return distributions also have some behavioral origins (investor excessive optimism or pessimism leading to large market moves) and are therefore studied in behavioral finance
.
In marketing
, the familiar 80-20 rule frequently found (e.g. "20% of customers account for 80% of the revenue") is a manifestation of a fat tail distribution underlying the data.
, political scientists Ian Bremmer
and Preston Keat
propose to apply the fat tail concept to geopolitics. As William Safire
notes in his etymology of the term, a fat tail occurs when there is an unexpectedly thick end or “tail” toward the edges of a distribution curve, indicating an irregularly high likelihood of catastrophic events. This represents the risks of a particular event occurring that are so unlikely to happen and difficult to predict that many choose to ignore their possibility. One example that Bremmer and Keat highlight in The Fat Tail is the August 1998 Russian devaluation and debt default. Leading up to this event, economic analysts predicted that Russia would not default because the country had both the ability and willingness to continue to make its payments. However, political analysts argued that Russia’s fragmented leadership and lack of market regulation—along with the fact that several powerful Russian officials would benefit from a default—reduced Russia’s willingness to pay. Since these political factors were missing from the economic models, the economists did not assign the correct probability to a Russian default.
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
that has the property, along with the heavy-tailed distribution
Heavy-tailed distribution
In probability theory, heavy-tailed distributions are probability distributions whose tails are not exponentially bounded: that is, they have heavier tails than the exponential distribution...
s, that they exhibit extremely large skewness
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
or kurtosis
Kurtosis
In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
. This comparison is often made relative to the ubiquitous normal distribution, which itself is an example of an exceptionally thin tail distribution, or to the exponential distribution
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
. Fat tail distributions have been empirically encountered in a fair number of areas: economics, physics, and earth sciences. Fat tail distributions have power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
decay in the tail of the distribution, but do not necessarily follow a power law everywhere.
Definition
The distribution of a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X is said to have a fat tail if
That is, if X has a probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
,
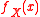,Here the notation "
" is the "twiddles" notation used for the asymptotic equivalence of functions. Some reserve the term "fat tail" for distributions only where 0 < α < 2 (i.e. only in cases with infinite variance).Fat tails and risk estimate distortions
By contrast to fat tail distributions, the normal distribution posits events that deviate from the meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
by five or more standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
s ("5-sigma event") are extremely rare, with 10- or more sigma being practically impossible. On the other hand, fat tail distributions such as the Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
(and all other stable distributions with the exception of the normal distribution) are examples of fat tail distributions that have "infinite sigma" (more technically: "the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
does not exist").
Thus when data naturally arise from a fat tail distribution, shoehorning the normal distribution model of risk—and an estimate of the corresponding sigma based necessarily on a finite sample size—would severely understate the true risk. Many—notably Benoît Mandelbrot
Benoît Mandelbrot
Benoît B. Mandelbrot was a French American mathematician. Born in Poland, he moved to France with his family when he was a child...
as well as Nassim Taleb
Nassim Taleb
Nassim Nicholas Taleb is a Lebanese American essayist whose work focuses on problems of randomness and probability. His 2007 book The Black Swan was described in a review by Sunday Times as one of the twelve most influential books since World War II....
—have noted this shortcoming of the normal distribution model and have proposed that fat tail distributions such as the stable distribution govern asset returns frequently found in finance
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
.
The Black–Scholes model of option pricing is based on a normal distribution. If the distribution is actually a fat-tailed one, then the model will under-price options
Option (finance)
In finance, an option is a derivative financial instrument that specifies a contract between two parties for a future transaction on an asset at a reference price. The buyer of the option gains the right, but not the obligation, to engage in that transaction, while the seller incurs the...
that are far out of the money
Moneyness
In finance, moneyness is a measure of the degree to which a derivative is likely to have positive monetary value at its expiration, in the risk-neutral measure. It can be measured in percentage probability, or in standard deviations....
, since a 5 or 7 sigma event is much more likely than the normal distribution would predict.
Applications in economics
In financeFinance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, fat tails are considered undesirable because of the additional risk
Risk
Risk is the potential that a chosen action or activity will lead to a loss . The notion implies that a choice having an influence on the outcome exists . Potential losses themselves may also be called "risks"...
they imply. For example, an investment strategy may have an expected return, after one year, that is five times its standard deviation. Assuming a normal distribution, the likelihood of its failure (negative return) is less than one in a million; in practice, it may be higher. Normal distributions that emerge in finance generally do so because the factors influencing an asset's value or price are mathematically "well-behaved", and the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
provides for such a distribution. However, traumatic "real-world" events (such as an oil shock, a large corporate bankruptcy, or an abrupt change in a political situation) are usually not mathematically well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
.
Historical examples include the Black Monday (1987)
Black Monday (1987)
In finance, Black Monday refers to Monday October 19, 1987, when stock markets around the world crashed, shedding a huge value in a very short time. The crash began in Hong Kong and spread west to Europe, hitting the United States after other markets had already declined by a significant margin...
, or the unpegging of some currencies.
Fat tails in market return distributions also have some behavioral origins (investor excessive optimism or pessimism leading to large market moves) and are therefore studied in behavioral finance
Behavioral finance
Behavioral economics and its related area of study, behavioral finance, use social, cognitive and emotional factors in understanding the economic decisions of individuals and institutions performing economic functions, including consumers, borrowers and investors, and their effects on market...
.
In marketing
Marketing
Marketing is the process used to determine what products or services may be of interest to customers, and the strategy to use in sales, communications and business development. It generates the strategy that underlies sales techniques, business communication, and business developments...
, the familiar 80-20 rule frequently found (e.g. "20% of customers account for 80% of the revenue") is a manifestation of a fat tail distribution underlying the data.
Applications in geopolitics
In The Fat Tail: The Power of Political Knowledge for Strategic InvestingThe Fat Tail: The Power of Political Knowledge for Strategic Investing
The Fat Tail: The Power of Political Knowledge for Strategic Investing is a book by political scientists Ian Bremmer and Preston Keat...
, political scientists Ian Bremmer
Ian Bremmer
Ian Bremmer is an American political scientist specializing in US foreign policy, states in transition, and global political risk. He is the president and founder of Eurasia Group, a leading global political risk research and consulting firm...
and Preston Keat
Preston Keat
Preston Keat is an American political scientist specializing on global political risk. He is a director of research and head of the Europe Practice of Eurasia Group, the global political risk consultancy. He also is the head of the Europe & Eurasia practice group, focusing on emerging markets in...
propose to apply the fat tail concept to geopolitics. As William Safire
William Safire
William Lewis Safire was an American author, columnist, journalist and presidential speechwriter....
notes in his etymology of the term, a fat tail occurs when there is an unexpectedly thick end or “tail” toward the edges of a distribution curve, indicating an irregularly high likelihood of catastrophic events. This represents the risks of a particular event occurring that are so unlikely to happen and difficult to predict that many choose to ignore their possibility. One example that Bremmer and Keat highlight in The Fat Tail is the August 1998 Russian devaluation and debt default. Leading up to this event, economic analysts predicted that Russia would not default because the country had both the ability and willingness to continue to make its payments. However, political analysts argued that Russia’s fragmented leadership and lack of market regulation—along with the fact that several powerful Russian officials would benefit from a default—reduced Russia’s willingness to pay. Since these political factors were missing from the economic models, the economists did not assign the correct probability to a Russian default.