Lévy distribution
Encyclopedia
In probability theory
and statistics
, the Lévy distribution, named after Paul Pierre Lévy
, is a continuous probability distribution for a non-negative random variable
. In spectroscopy
this distribution, with frequency as the dependent variable, is known as a van der Waals profile."van der Waals profile" appears with lowercase "van" in almost all sources, such as: Statistical mechanics of the liquid surface by Clive Anthony Croxton, 1980, A Wiley-Interscience publication, ISBN 0471276634, 9780471276630, http://books.google.it/books?id=Wve2AAAAIAAJ&q=%22Van+der+Waals+profile%22&dq=%22Van+der+Waals+profile%22&hl=en; and in Journal of technical physics, Volume 36, by Instytut Podstawowych Problemów Techniki (Polska Akademia Nauk), publisher: Państwowe Wydawn. Naukowe., 1995, http://books.google.it/books?id=2XpVAAAAMAAJ&q=%22Van+der+Waals+profile%22&dq=%22Van+der+Waals+profile%22&hl=en It is a special case of the inverse-gamma distribution.
It is one of the few distributions that are stable
and that have probability density function
s that are analytically expressible, the others being the normal distribution and the Cauchy distribution
. All three are special cases of the stable distributions, which does not generally have an analytically expressible probability density function.
of the Lévy distribution over the domain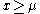 is
is
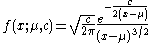
where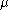 is the location parameter and
is the location parameter and  is the scale parameter
is the scale parameter
. The cumulative distribution function is
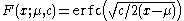
where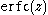 is the complementary error function
is the complementary error function
. The shift parameter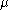 has the effect of shifting the curve to the right by an amount
has the effect of shifting the curve to the right by an amount 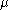 , and changing the support to the interval [
, and changing the support to the interval [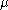 ,
, 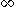 ). Like all stable distributions, the Levy distribution has a standard form f(x;0,1) which has the following property:
). Like all stable distributions, the Levy distribution has a standard form f(x;0,1) which has the following property:
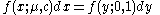
where y is defined as
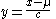
The characteristic function
of the Lévy distribution is given by
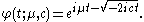
Note that the characteristic function can also be written in the same form used for the stable distribution with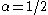 and
and 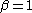 :
:
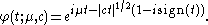
Assuming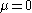 , the nth moment
, the nth moment
of the unshifted Lévy distribution is formally defined by:

which diverges for all n > 0 so that the moments of the Lévy distribution do not exist. The moment generating function is then formally defined by:
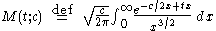
which diverges for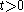 and is therefore not defined in an interval around zero, so that the moment generating function is not defined per se. Like all stable distributions except the normal distribution, the wing of the probability density function exhibits heavy tail behavior falling off according to a power law:
and is therefore not defined in an interval around zero, so that the moment generating function is not defined per se. Like all stable distributions except the normal distribution, the wing of the probability density function exhibits heavy tail behavior falling off according to a power law:
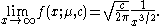
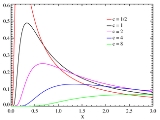
This is illustrated in the diagram below, in which the probability density functions for various values of c and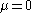 are plotted on a log-log scale.
are plotted on a log-log scale.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Lévy distribution, named after Paul Pierre Lévy
Paul Pierre Lévy
Paul Pierre Lévy was a Jewish French mathematician who was active especially in probability theory, introducing martingales and Lévy flights...
, is a continuous probability distribution for a non-negative random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
. In spectroscopy
Spectroscopy
Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
this distribution, with frequency as the dependent variable, is known as a van der Waals profile."van der Waals profile" appears with lowercase "van" in almost all sources, such as: Statistical mechanics of the liquid surface by Clive Anthony Croxton, 1980, A Wiley-Interscience publication, ISBN 0471276634, 9780471276630, http://books.google.it/books?id=Wve2AAAAIAAJ&q=%22Van+der+Waals+profile%22&dq=%22Van+der+Waals+profile%22&hl=en; and in Journal of technical physics, Volume 36, by Instytut Podstawowych Problemów Techniki (Polska Akademia Nauk), publisher: Państwowe Wydawn. Naukowe., 1995, http://books.google.it/books?id=2XpVAAAAMAAJ&q=%22Van+der+Waals+profile%22&dq=%22Van+der+Waals+profile%22&hl=en It is a special case of the inverse-gamma distribution.
It is one of the few distributions that are stable
Stability (probability)
In probability theory, the stability of a random variable is the property that a linear combination of two independent copies of the variable has the same distribution, up to location and scale parameters. The distributions of random variables having this property are said to be "stable...
and that have probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s that are analytically expressible, the others being the normal distribution and the Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
. All three are special cases of the stable distributions, which does not generally have an analytically expressible probability density function.
Definition
The probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of the Lévy distribution over the domain
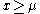 is
is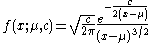
where
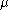 is the location parameter and
is the location parameter and  is the scale parameter
is the scale parameterScale parameter
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
. The cumulative distribution function is
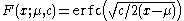
where
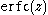 is the complementary error function
is the complementary error functionError function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
. The shift parameter
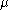 has the effect of shifting the curve to the right by an amount
has the effect of shifting the curve to the right by an amount 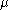 , and changing the support to the interval [
, and changing the support to the interval [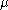 ,
, 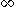 ). Like all stable distributions, the Levy distribution has a standard form f(x;0,1) which has the following property:
). Like all stable distributions, the Levy distribution has a standard form f(x;0,1) which has the following property: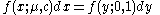
where y is defined as
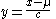
The characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
of the Lévy distribution is given by
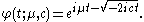
Note that the characteristic function can also be written in the same form used for the stable distribution with
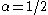 and
and 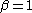 :
: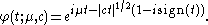
Assuming
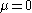 , the nth moment
, the nth momentMoment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of the unshifted Lévy distribution is formally defined by:

which diverges for all n > 0 so that the moments of the Lévy distribution do not exist. The moment generating function is then formally defined by:
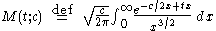
which diverges for
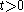 and is therefore not defined in an interval around zero, so that the moment generating function is not defined per se. Like all stable distributions except the normal distribution, the wing of the probability density function exhibits heavy tail behavior falling off according to a power law:
and is therefore not defined in an interval around zero, so that the moment generating function is not defined per se. Like all stable distributions except the normal distribution, the wing of the probability density function exhibits heavy tail behavior falling off according to a power law: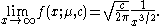
This is illustrated in the diagram below, in which the probability density functions for various values of c and
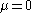 are plotted on a log-log scale.
are plotted on a log-log scale.Related distributions
- If
 then
then 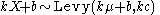
- If
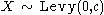 then
then  (inverse gamma distribution)
(inverse gamma distribution) - Lévy distribution is a special case of type 5 Pearson distributionPearson distributionThe Pearson distribution is a family of continuous probability distributions. It was first published by Karl Pearson in 1895 and subsequently extended by him in 1901 and 1916 in a series of articles on biostatistics.- History :...
- If
 (Normal distribution) then
(Normal distribution) then 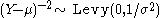
- If
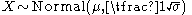 then
then 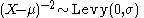
- If
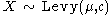 then
then 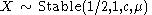 (Stable distribution)
(Stable distribution) - If
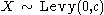 then
then 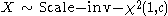 (Scaled-inverse-chi-squared distribution)
(Scaled-inverse-chi-squared distribution) - If
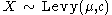 then
then 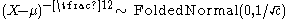 (Folded normal distributionFolded Normal DistributionThe folded normal distribution is a probability distribution related to the normal distribution. Given a normally distributed random variable X with mean μ and variance σ2, the random variable Y = |X| has a folded normal distribution. Such a case may be encountered if only the magnitude of some...
(Folded normal distributionFolded Normal DistributionThe folded normal distribution is a probability distribution related to the normal distribution. Given a normally distributed random variable X with mean μ and variance σ2, the random variable Y = |X| has a folded normal distribution. Such a case may be encountered if only the magnitude of some...
)
Applications
- The frequency of geomagnetic reversalGeomagnetic reversalA geomagnetic reversal is a change in the Earth's magnetic field such that the positions of magnetic north and magnetic south are interchanged. The Earth's field has alternated between periods of normal polarity, in which the direction of the field was the same as the present direction, and reverse...
s appears to follow a Lévy distribution - The time of hittingHitting timeIn the study of stochastic processes in mathematics, a hitting time is a particular instance of a stopping time, the first time at which a given process "hits" a given subset of the state space...
a single point (different from the starting point 0) by the Brownian motionWiener processIn mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
(different from the starting point 0) by the Brownian motionWiener processIn mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
has the Lévy distribution with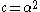 . (For a Brownian motion with drift, this time may follow an inverse Gaussian distributionInverse Gaussian distribution| cdf = \Phi\left +\exp\left \Phi\left...
. (For a Brownian motion with drift, this time may follow an inverse Gaussian distributionInverse Gaussian distribution| cdf = \Phi\left +\exp\left \Phi\left...
, which has the Lévy distribution as a limit.)
- The length of the path followed by a photon in a turbid medium follows the Lévy distribution.

