Pearson distribution - AbsoluteAstronomy.com

The Pearson distribution is a family of continuous probability distribution

Probability distribution

In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....

s. It was first published by Karl Pearson

Karl Pearson

Karl Pearson FRS was an influential English mathematician who has been credited for establishing the disciplineof mathematical statistics....

in 1895 and subsequently extended by him in 1901 and 1916 in a series of articles on biostatistics

Biostatistics

Biostatistics is the application of statistics to a wide range of topics in biology...

History

The Pearson system was originally devised in an effort to model visibly skew

Skewness

In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...

ed observations. It was well known at the time how to adjust a theoretical model to fit the first two cumulant

Cumulant

In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...

s or moment

Moment (mathematics)

In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...

s of observed data: Any probability distribution

Probability distribution

In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....

can be extended straightforwardly to form a location-scale family

Location-scale family

In probability theory, especially as that field is used in statistics, a location-scale family is a family of univariate probability distributions parametrized by a location parameter and a non-negative scale parameter; if X is any random variable whose probability distribution belongs to such a...

. Except in pathological

Pathological (mathematics)

In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....

cases, a location-scale family can be made to fit the observed mean (first cumulant) and variance

Variance

In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...

(second cumulant) arbitrarily well. However, it was not known how to construct probability distributions in which the skewness

Skewness

(standardized third cumulant) and kurtosis

Kurtosis

In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...

(standardized fourth cumulant) could be adjusted equally freely. This need became apparent when trying to fit known theoretical models to observed data that exhibited skewness. Pearson's examples include survival data, which are usually asymmetric.

In his original paper, Pearson (1895, p. 360) identified four types of distributions (numbered I through IV) in addition to the normal distribution (which was originally known as type V). The classification depended on whether the distributions were support

Support (mathematics)

In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...

ed on a bounded interval, on a half-line, or on the whole real line

Real line

In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...

; and whether they were potentially skewed or necessarily symmetric. A second paper (Pearson 1901) fixed two omissions: it redefined the type V distribution (originally just the normal distribution, but now the inverse-gamma distribution) and introduced the type VI distribution. Together the first two papers cover the five main types of the Pearson system (I, III, VI, V, and IV). In a third paper, Pearson (1916) introduced further special cases and subtypes (VII through XII).

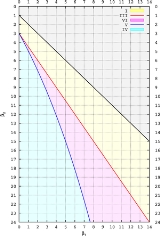
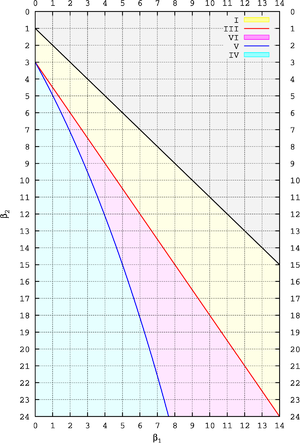
Rhind (1909, pp. 430–432) devised a simple way of visualizing the parameter space of the Pearson system, which was subsequently adopted by Pearson (1916, plate 1 and pp. 430ff., 448ff.). The Pearson types are characterized by two quantities, commonly referred to as

and

. The first is the square of the skewness

Skewness

where

is the skewness, or third standardized moment. The second is the traditional kurtosis

Kurtosis

In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...

, or fourth standardized moment:

. (Modern treatments define kurtosis

in terms of cumulants instead of moments, so that for a normal distribution we have

and

. Here we follow the historical precedent and use

.) The diagram on the right shows which Pearson type a given concrete distribution (identified by a point

) belongs to.

Many of the skewed and/or non-mesokurtic distributions familiar to us today were still unknown in the early 1890s. What is now known as the beta distribution had been used by Thomas Bayes

Thomas Bayes

Thomas Bayes was an English mathematician and Presbyterian minister, known for having formulated a specific case of the theorem that bears his name: Bayes' theorem...

as a posterior distribution of the parameter of a Bernoulli distribution in his 1763 work on inverse probability

Inverse probability

In probability theory, inverse probability is an obsolete term for the probability distribution of an unobserved variable.Today, the problem of determining an unobserved variable is called inferential statistics, the method of inverse probability is called Bayesian probability, the "distribution"...

. The Beta distribution gained prominence due to its membership in Pearson's system and was known until the 1940s as the Pearson type I distribution.

(Pearson's type II distribution is a special case of type I, but is usually no longer singled out.) The gamma distribution originated from Pearson's work (Pearson 1893, p. 331; Pearson 1895, pp. 357, 360, 373–376) and was known as the Pearson type III distribution, before acquiring its modern name in the 1930s and 1940s.

Pearson's 1895 paper introduced the type IV distribution, which contains Student's t-distribution as a special case, predating William Sealy Gosset

William Sealy Gosset

William Sealy Gosset is famous as a statistician, best known by his pen name Student and for his work on Student's t-distribution....

's subsequent use by several years. His 1901 paper introduced the inverse-gamma distribution (type V) and the beta prime distribution (type VI).

Definition

A Pearson density

Probability density function

In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...

p is defined to be any valid solution to the differential equation

Differential equation

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

(cf. Pearson 1895, p. 381)

with :

According to Ord, Pearson devised the underlying form of Equation (1) on the basis of, firstly, the formula for the derivative of the logarithm of the density function of the normal distribution (which gives a linear function) and, secondly, from a recurrence relation for values in the probability mass function

Probability mass function

In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...

of the hypergeometric distribution (which yields the linear-divided-by-quadratic structure).

In Equation (1), the parameter a determines a stationary point

Stationary point

In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....

, and hence under some conditions a mode

Mode (statistics)

In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....

of the distribution, since

follows directly from the differential equation.

Since we are confronted with a linear differential equation with variable coefficients, its solution is straightforward:

The integral in this solution simplifies considerably when certain special cases of the integrand are considered. Pearson (1895, p. 367) distinguished two main cases, determined by the sign of the discriminant

Discriminant

In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....

(and hence the number of real roots) of the quadratic function

Quadratic function

A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....

Case 1, negative discriminant: The Pearson type IV distribution

If the discriminant of the quadratic function (2) is negative (

), it has no real roots. Then define

and

Observe that

is a well-defined real number and

, because by assumption

and therefore

. Applying these substitutions, the quadratic function (2) is transformed into

The absence of real roots is obvious from this formulation, because

is necessarily positive.

We now express the solution to the differential equation (1) as a function of y:

Pearson (1895, p. 362) called this the "trigonometrical case", because the integral

involves the inverse

Inverse trigonometric function

In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions with suitably restricted domains .The notations sin−1, cos−1, etc...

trigonometric

Trigonometric function

In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...

arctan function. Then

Finally, let

and

Applying these substitutions, we obtain the parametric function:

This unnormalized density has support

Support (mathematics)

In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...

on the entire real line

Real line

. It depends on a scale parameter

Scale parameter

In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...

and shape parameter

Shape parameter

In probability theory and statistics, a shape parameter is a kind of numerical parameter of a parametric family of probability distributions.- Definition :...

and

. One parameter was lost when we chose to find the solution to the differential equation (1) as a function of y rather than x. We therefore reintroduce a fourth parameter, namely the location parameter

Location parameter

In statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...

λ. We have thus derived the density of the Pearson type IV distribution:

The normalizing constant

Normalizing constant

The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...

involves the complex Gamma function

Gamma function

In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...

(Γ) and the Beta function (B).

The Pearson type VII distribution

The shape parameter ν of the Pearson type IV distribution controls its skewness

Skewness

. If we fix its value at zero, we obtain a symmetric three-parameter family. This special case is known as the Pearson type VII distribution (cf. Pearson 1916, p. 450). Its density is

where B is the Beta function.

An alternative parameterization (and slight specialization) of the type VII distribution is obtained by letting

which requires

. This entails a minor loss of generality but ensures that the variance

Variance

of the distribution exists and is equal to

. Now the parameter m only controls the kurtosis

Kurtosis

In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...

of the distribution. If m approaches infinity as λ and σ are held constant, the normal distribution arises as a special case:

This is the density of a normal distribution with mean λ and standard deviation σ.

It is convenient to require that

and to let

This is another specialization, and it guarantees that the first four moments of the distribution exist. More specifically, the Pearson type VII distribution parameterized in terms of

has a mean of λ, standard deviation

Standard deviation

Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...

of σ, skewness

Skewness

of zero, and excess kurtosis of

Student's t-distribution

The Pearson type VII distribution subsumes Student's t-distribution, and hence also the Cauchy distribution

Cauchy distribution

The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...

. Student's t-distribution arises as the result of applying the following substitutions to its original parameterization:

and

where

. Observe that the constraint

is satisfied. The density of this restricted one-parameter family is

which is easily recognized as the density of Student's t-distribution.

Case 2, non-negative discriminant

If the quadratic function (2) has a non-negative discriminant (

), it has real roots a₁ and a₂ (not necessarily distinct):

In the presence of real roots the quadratic function (2) can be written as

and the solution to the differential equation is therefore

Pearson (1895, p. 362) called this the "logarithmic case", because the integral

involves only the logarithm

Logarithm

The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...

function, and not the arctan function as in the previous case.

Using the substitution

we obtain the following solution to the differential equation (1):

Since this density is only known up to a hidden constant of proportionality, that constant can be changed and the density written as follows:

The Pearson type I and type II distribution

The Pearson type I distribution (a generalization of the beta distribution) arises when the roots of the quadratic equation (2) are of opposite sign, that is,

. Then the solution p is supported on the interval

. Apply the substitution

which yields a solution in terms of y that is supported on the interval

One may define:

Regrouping constants and parameters, this simplifies to:

Thus

follows a

with

It turns out that

is necessary and sufficient for p to be a proper probability density function.

The Pearson type II distribution

The Pearson type II distribution is a special case of the Pearson type I family restricted to symmetric distributions.

For the Pearson Type II Curve
,

where

the ordinate, y, is the frequency of

. The Pearson Type II Curve is used in computing the table of significant correlation coefficients for Spearman's rank correlation coefficient

Spearman's rank correlation coefficient

In statistics, Spearman's rank correlation coefficient or Spearman's rho, named after Charles Spearman and often denoted by the Greek letter \rho or as r_s, is a non-parametric measure of statistical dependence between two variables. It assesses how well the relationship between two variables can...

when the number of items in a series is less than 100 (or 30, depending on some sources). After that, the distribution mimics a standard Student's t-distribution. For the table of values, certain values are used as the constants in the previous equation:

The moments of x used are

The Pearson type III distribution

The Pearson type III distribution is a gamma distribution or chi-squared distribution.

The Pearson type V distribution

Defining new parameters:

follows an

The Pearson type V distribution is an inverse-gamma distribution.

The Pearson type VI distribution

follows a :

The Pearson type VI distribution is a beta prime distribution or F-distribution.

Relation to other distributions

The Pearson family subsumes the following distributions, among others:

beta distribution (type I)
beta prime distribution (type VI)
Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...

(type IV)
chi-squared distribution (type III)
continuous uniform distribution
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...

(limit of type I)
exponential distribution
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...

(type III)
gamma distribution (type III)
F-distribution (type VI)
inverse-chi-squared distribution (type V)
inverse-gamma distribution (type V)
normal distribution (limit of type I, III, IV, V, or VI)
Student's t-distribution (type VII, which is the non-skewed subtype of type IV)

Applications

These models are used in financial markets, given their ability to be parametrised in a way that has intuitive meaning for market traders. A number of models are in current use that capture the stochastic nature of the volatility of rates, stocks etc. and this family of distributions may prove to be one of the more important.

In the United States, the Log-Pearson III is the default distribution for flood frequency analysis.

Secondary sources

Milton Abramowitz and Irene A. Stegun (1964). Handbook of Mathematical Functions
Handbook of mathematical functions
*Abramowitz and Stegun, the informal name for Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables*NIST Handbook of Mathematical Functions...

with Formulas, Graphs, and Mathematical Tables. National Bureau of Standards.

Eric W. Weisstein
Eric W. Weisstein
Eric W. Weisstein is an encyclopedist who created and maintains MathWorld and Eric Weisstein's World of Science . He currently works for Wolfram Research, Inc.-Education:...

et al. Pearson Type III Distribution. From MathWorld
MathWorld
MathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...

.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.