
Standardized moment
Encyclopedia
In probability theory
and statistics
, the kth
standardized moment of a probability distribution
is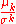 where
where  is the kth moment about the mean and σ is the standard deviation
is the kth moment about the mean and σ is the standard deviation
.
It is the normalization
of the kth moment with respect to standard deviation
. The power of k is because moments scale as , meaning that
, meaning that  : they are homogeneous polynomial
: they are homogeneous polynomial
s of degree k, thus the standardized moment is scale invariant. This can also be understood as being because moments have dimension, but in the ratio defining standardized moments, the dimensions cancel, so they are dimensionless numbers.
Note that for skewness and kurtosis alternative definitions exist, which are based on the third and fourth cumulant
respectively.
, . However, this is not a standardized moment, firstly because it is a reciprocal, and secondly because
. However, this is not a standardized moment, firstly because it is a reciprocal, and secondly because  is the first moment about zero (the mean), not the first moment about the mean (which is zero).
is the first moment about zero (the mean), not the first moment about the mean (which is zero).
See Normalization (statistics)
for further normalizing ratios.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the kth
standardized moment of a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
is
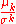 where
where  is the kth moment about the mean and σ is the standard deviation
is the kth moment about the mean and σ is the standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
.
It is the normalization
Normalization (statistics)
In one usage in statistics, normalization is the process of isolating statistical error in repeated measured data. A normalization is sometimes based on a property...
of the kth moment with respect to standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
. The power of k is because moments scale as
 , meaning that
, meaning that  : they are homogeneous polynomial
: they are homogeneous polynomialHomogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
s of degree k, thus the standardized moment is scale invariant. This can also be understood as being because moments have dimension, but in the ratio defining standardized moments, the dimensions cancel, so they are dimensionless numbers.
- The first standardized moment is zero, because the first moment about the mean is zero
- The second standardized moment is one, because the second moment about the mean is equal to the varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
(the square of the standard deviation) - The third standardized moment is the skewnessSkewnessIn probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
- The fourth standardized moment is the kurtosisKurtosisIn probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
Note that for skewness and kurtosis alternative definitions exist, which are based on the third and fourth cumulant
Cumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
respectively.
Other normalizations
Another scale invariant, dimensionless measure for characteristics of a distribution is the coefficient of variationCoefficient of variation
In probability theory and statistics, the coefficient of variation is a normalized measure of dispersion of a probability distribution. It is also known as unitized risk or the variation coefficient. The absolute value of the CV is sometimes known as relative standard deviation , which is...
,
 . However, this is not a standardized moment, firstly because it is a reciprocal, and secondly because
. However, this is not a standardized moment, firstly because it is a reciprocal, and secondly because  is the first moment about zero (the mean), not the first moment about the mean (which is zero).
is the first moment about zero (the mean), not the first moment about the mean (which is zero).See Normalization (statistics)
Normalization (statistics)
In one usage in statistics, normalization is the process of isolating statistical error in repeated measured data. A normalization is sometimes based on a property...
for further normalizing ratios.
See also
- Coefficient of variationCoefficient of variationIn probability theory and statistics, the coefficient of variation is a normalized measure of dispersion of a probability distribution. It is also known as unitized risk or the variation coefficient. The absolute value of the CV is sometimes known as relative standard deviation , which is...
- Moment (mathematics)Moment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
- Standard score: Other normalizations

