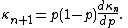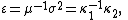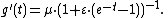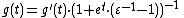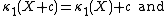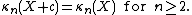Cumulant
Encyclopedia
In probability theory
and statistics
, the cumulants κn of a probability distribution
are a set of quantities that provide an alternative to the moments
of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have identical cumulants as well, and similarly the cumulants determine the moments. In some cases theoretical treatments of problems in terms of cumulants are simpler than those using moments.
Just as for moments, where joint moments are used for collections of random variables, it is possible to define joint cumulants.
using the (non-central) moments μ′n of X and the moment-generating function
,
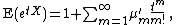
with a formal power series
logarithm: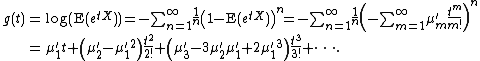
The cumulants of a distribution are closely related to the distribution's moments
. For example, if a random variable
X admits an expected value
μ = E(X) and a variance
σ2 = E((X − μ)2), then these are the first two cumulants: μ = κ1 and σ2 = κ2.
Generally, the cumulants can be extracted from the cumulant-generating function via differentiation (at zero) of g(t). That is, the cumulants appear as the coefficients in the Maclaurin series of g(t):
Note that expectation values are sometimes denoted by angle brackets, e.g.,
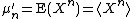
and cumulants can be denoted by angle brackets with the subscript c, e.g.,
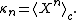
Some writers prefer to define the cumulant generating function as the natural logarithm of the characteristic function
, which is sometimes also called the second characteristic function,
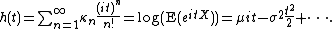
The advantage of h(t)—in some sense the function g(t) evaluated for (purely) imaginary arguments—is that E(eitX) will be well defined for all real values of t even when E(etX) is not well defined for all real values of t, such as can occur when there is "too much" probability that X has a large magnitude. Although h(t) will be well defined, it nonetheless may mimic g(t) by not having a Maclaurin series beyond (or, rarely, even to) linear order in the argument t. Thus, many cumulants may still not be well defined. Nevertheless, even when h(t) does not have a long Maclaurin series it can be used directly in analyzing and, particularly, adding random variables. Both the Cauchy distribution
(also called the Lorentzian) and stable distribution (related to the Lévy distribution) are examples of distributions for which the generating functions do not have power-series expansions.
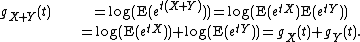
so that each cumulant of a sum is the sum of the corresponding cumulants of the addends.
A distribution with given cumulants κn can be approximated through an Edgeworth series
.
Introducing the variance-to-mean ratio
the above probability distributions get a unified formula for the derivative of the cumulant generating function:
The second derivative is
confirming that the first cumulant is κ1 = g '(0) = μ and the second cumulant is κ2 = g ' '(0) = μ·ε.
The constant random variables X = μ have є = 0. The binomial distributions have ε = 1 − p so that 0 < ε < 1. The Poisson distributions have ε = 1. The negative binomial distributions have ε = p−1 so that ε > 1. Note the analogy to the classification of conic sections by eccentricity
: circles ε = 0, ellipses 0 < ε < 1, parabolas ε = 1, hyperbolas ε > 1.
. If g(t) is finite for a range t1 < Re(t) < t2 then if t1 < 0 < t2 then g(t) is analytic and infinitely differentiable for t1 < Re(t) < t2. Moreover for t real and t1 < t < t2 g(t) is strictly convex, and g' (t) is strictly increasing.
; all of the others are shift-invariant
. This means that, if we denote by κn(X) the nth cumulant of the probability distribution of the random variable X, then for any constant c:
In other words, shifting a random variable (adding c) shifts the first cumulant (the mean) and doesn't affect any of the others.
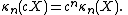
random variables then κn(X + Y) = κn(X) + κn(Y).
κm = κm+1 = ... = 0 for some m > 3, with the lower-order cumulants (orders 3 to m − 1) being non-zero. There are no such distributions. The underlying result here is that the cumulant generating function cannot be a finite-order polynomial of degree greater than 2.
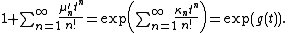
So the cumulant generating function is the logarithm of the moment generating function.
The first cumulant is the expected value
; the second and third cumulants are respectively the second and third central moment
s (the second central moment is the variance
); but the higher cumulants are neither moments nor central moments, but rather more complicated polynomial functions of the moments.
The cumulants are related to the moments
by the following recursion
formula:
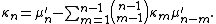
The nth moment
μ′n is an nth-degree polynomial in the first n cumulants:
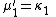
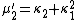
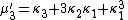
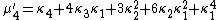
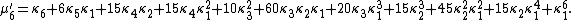
The coefficients are precisely those that occur in Faà di Bruno's formula
.
The "prime" distinguishes the moments μ′n from the central moments μn. To express the central moments as functions of the cumulants, just drop from these polynomials all terms in which κ1 appears as a factor:
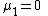
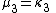
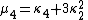
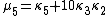
Likewise, the nth cumulant κn is an nth-degree polynomial in the first n non-central moments:
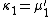
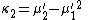
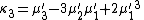
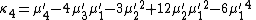
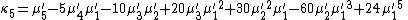
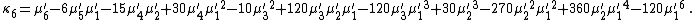
To express the cumulants κn for n > 1 as functions of the central moments, drop from these polynomials all terms in which μ'1 appears as a factor:
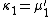
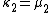
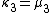
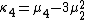
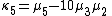
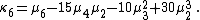
interpretation: the coefficients count certain partitions of sets
. A general form of these polynomials is
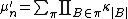
where
Thus each monomial
is a constant times a product of cumulants in which the sum of the indices is n (e.g., in the term κ3 κ22 κ1, the sum of the indices is 3 + 2 + 2 + 1 = 8; this appears in the polynomial that expresses the 8th moment as a function of the first eight cumulants). A partition of the integer
n corresponds to each term. The coefficient in each term is the number of partitions of a set of n members that collapse to that partition of the integer n when the members of the set become indistinguishable.
A consequence is that
where π runs through the list of all partitions of { 1, ..., n }, B runs through the list of all blocks of the partition π, and |π| is the number of parts in the partition. For example,
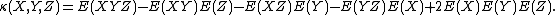
If any of these random variables are identical, e.g. if X = Y, then the same formulae apply, e.g.
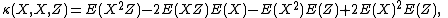
although for such repeated variables there are more concise formulae. For zero-mean random vectors,
The joint cumulant of just one random variable is its expected value, and that of two random variables is their covariance
. If some of the random variables are independent of all of the others, then any cumulant involving two (or more) independent random variables is zero. If all n random variables are the same, then the joint cumulant is the nth ordinary cumulant.
The combinatorial meaning of the expression of moments in terms of cumulants is easier to understand than that of cumulants in terms of moments:
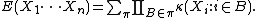
For example:
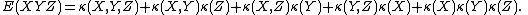
Another important property of joint cumulants is multilinearity:
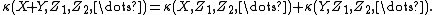
Just as the second cumulant is the variance, the joint cumulant of just two random variables is the covariance
. The familiar identity
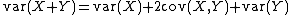
generalizes to cumulants:
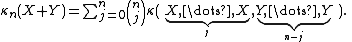
and the law of total variance
generalize naturally to conditional cumulants. The case n = 3, expressed in the language of (central) moments
rather than that of cumulants, says
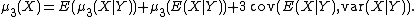
The general result stated below first appeared in 1969 in The Calculation of Cumulants via Conditioning by David R. Brillinger in volume 21 of Annals of the Institute of Statistical Mathematics, pages 215–218.
In general, we have
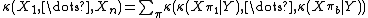
where
many extensive quantities – that is quantities that are proportional to the volume or size of a given system – are related to cumulants of random variables. The deep connection is that in a large system an extensive quantity like the energy or number of particles can be thought of as the sum of (say) the energy associated with a number of nearly independent regions. The fact that the cumulants of these nearly independent random variables will (nearly) add make it reasonable that extensive quantities should be expected to be related to cumulants.
A system in equilibrium with a thermal bath at temperature T can occupy states of energy E. The energy E can be considered a random variable, having the probability density. The partition function
of the system is
where β = 1/(kT) and k is Boltzmann's constant and the notation
has been used rather than 
for the expectation value to avoid confusion with the energy, E. The Helmholtz free energy
is then
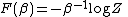
and is clearly very closely related to the cumulant generating function for the energy. The free energy gives access to all of the thermodynamics properties of the system via its first second and higher order derivatives, such as its internal energy
, entropy
, and specific heat. Because of the relationship between the free energy and the cumulant generating function, all these quantities are related to cumulants e.g. the energy and specific heat are given by
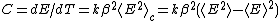
and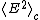
symbolizes the second cumulant of the energy. Other free energy is often also a function of other variables such as the magnetic field or chemical potential 
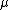, e.g.
where N is the number of particles and
is the grand potential. Again the close relationship between the definition of the free energy and the cumulant generating function implies that various derivatives of this free energy can be written in terms of joint cumulants of E and N.
Cumulants were first introduced by Thorvald N. Thiele
, in 1889, who called them semi-invariants. They were first called cumulants in a 1932 paper by Ronald Fisher
and John Wishart
. Fisher was publicly reminded of Thiele's work by Neyman, who also notes previous published citations of Thiele brought to Fisher's attention. Stephen Stigler
has said that the name cumulant was suggested to Fisher in a letter from Harold Hotelling
. In a paper published in 1929, Fisher had called them cumulative moment functions. The partition function in statistical physics was introduced by Josiah Willard Gibbs
in 1901. The free energy is often called Gibbs free energy. In statistical mechanics
, cumulants are also known as Ursell function
s relating to a publication in 1927.
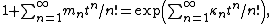
where the values of κn for n = 1, 2, 3, ... are found formally, i.e., by algebra alone, in disregard of questions of whether any series converges. All of the difficulties of the "problem of cumulants" are absent when one works formally. The simplest example is that the second cumulant of a probability distribution must always be nonnegative, and is zero only if all of the higher cumulants are zero. Formal cumulants are subject to no such constraints.
, the nth Bell number
is the number of partitions of a set of size n. All of the cumulants of the sequence of Bell numbers are equal to 1. The Bell numbers are the moments of the Poisson distribution with expected value
1.
in a field
of characteristic zero, being considered formal cumulants, there is a corresponding sequence { μ ′ : n = 1, 2, 3, ... } of formal moments, given by the polynomials above. For those polynomials, construct a polynomial sequence
in the following way. Out of the polynomial
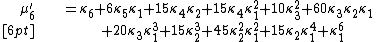
make a new polynomial in these plus one additional variable x:
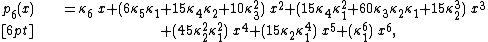
and then generalize the pattern. The pattern is that the numbers of blocks in the aforementioned partitions are the exponents on x. Each coefficient is a polynomial in the cumulants; these are the Bell polynomials, named after Eric Temple Bell
.
This sequence of polynomials is of binomial type. In fact, no other sequences of binomial type exist; every polynomial sequence of binomial type is completely determined by its sequence of formal cumulants.
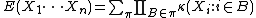
one sums over all partitions of the set { 1, ..., n }. If instead, one sums only over the noncrossing partition
s, then one gets "free cumulants" rather than conventional cumulants treated above. These play a central role in free probability
theory. In that theory, rather than considering independence
of random variable
s, defined in terms of Cartesian product
s of algebras
of random variables, one considers instead "freeness" of random variables, defined in terms of free product
s of algebras rather than Cartesian products of algebras.
The ordinary cumulants of degree higher than 2 of the normal distribution are zero. The free cumulants of degree higher than 2 of the Wigner semicircle distribution are zero. This is one respect in which the role of the Wigner distribution in free probability theory is analogous to that of the normal distribution in conventional probability theory.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the cumulants κn of a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
are a set of quantities that provide an alternative to the moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have identical cumulants as well, and similarly the cumulants determine the moments. In some cases theoretical treatments of problems in terms of cumulants are simpler than those using moments.
Just as for moments, where joint moments are used for collections of random variables, it is possible to define joint cumulants.
Introduction
The cumulants κn of a random variable X are defined via the cumulant-generating functionusing the (non-central) moments μ′n of X and the moment-generating function
Moment-generating function
In probability theory and statistics, the moment-generating function of any random variable is an alternative definition of its probability distribution. Thus, it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or...
,
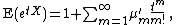
with a formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
logarithm:
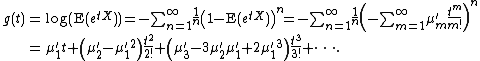
The cumulants of a distribution are closely related to the distribution's moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
. For example, if a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X admits an expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
μ = E(X) and a variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
σ2 = E((X − μ)2), then these are the first two cumulants: μ = κ1 and σ2 = κ2.
Generally, the cumulants can be extracted from the cumulant-generating function via differentiation (at zero) of g(t). That is, the cumulants appear as the coefficients in the Maclaurin series of g(t):
Note that expectation values are sometimes denoted by angle brackets, e.g.,
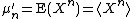
and cumulants can be denoted by angle brackets with the subscript c, e.g.,
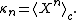
Some writers prefer to define the cumulant generating function as the natural logarithm of the characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
, which is sometimes also called the second characteristic function,
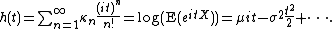
The advantage of h(t)—in some sense the function g(t) evaluated for (purely) imaginary arguments—is that E(eitX) will be well defined for all real values of t even when E(etX) is not well defined for all real values of t, such as can occur when there is "too much" probability that X has a large magnitude. Although h(t) will be well defined, it nonetheless may mimic g(t) by not having a Maclaurin series beyond (or, rarely, even to) linear order in the argument t. Thus, many cumulants may still not be well defined. Nevertheless, even when h(t) does not have a long Maclaurin series it can be used directly in analyzing and, particularly, adding random variables. Both the Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
(also called the Lorentzian) and stable distribution (related to the Lévy distribution) are examples of distributions for which the generating functions do not have power-series expansions.
Uses in mathematical statistics
Working with cumulants can have an advantage over using moments because for independent variables X and Y,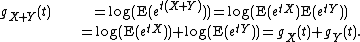so that each cumulant of a sum is the sum of the corresponding cumulants of the addends.
A distribution with given cumulants κn can be approximated through an Edgeworth series
Edgeworth series
The Gram–Charlier A series , and the Edgeworth series are series that approximate a probability distribution in terms of its cumulants...
.
Cumulants of some discrete probability distributions
- The constant random variable X = 1. The derivative of the cumulant generating function is g '(t) = 1. The first cumulant is κ1 = g '(0) = 1 and the other cumulants are zero, κ2 = κ3 = κ4 = ... = 0.
- The constant random variables X = μ. Every cumulant is just μ times the corresponding cumulant of the constant random variable X = 1. The derivative of the cumulant generating function is g '(t) = μ. The first cumulant is κ1 = g '(0) = μ and the other cumulants are zero, κ2 = κ3 = κ4 = ... = 0. So the derivative of cumulant generating functions is a generalizationGeneralizationA generalization of a concept is an extension of the concept to less-specific criteria. It is a foundational element of logic and human reasoning. Generalizations posit the existence of a domain or set of elements, as well as one or more common characteristics shared by those elements. As such, it...
of the real constants.
- The Bernoulli distributions, (number of successes in one trial with probability p of success). The special case p = 1 is the constant random variable X = 1. The derivative of the cumulant generating function is g '(t) = ((p −1−1)·e−t + 1)−1. The first cumulants are κ1 = g '(0) = p and κ2 = g ' '(0) = p·(1 − p) . The cumulants satisfy a recursion formula
- The geometric distributions, (number of failures before one success with probability p of success on each trial). The derivative of the cumulant generating function is g '(t) = ((1 − p)−1·e−t − 1)−1. The first cumulants are κ1 = g '(0) = p−1 − 1, and κ2 = g ' '(0) = κ1·p − 1. Substituting p = (μ+1)−1 gives g '(t) = ((μ−1 + 1)·e−t − 1)−1 and κ1 = μ.
- The Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
s. The derivative of the cumulant generating function is g '(t) = μ·et. All cumulants are equal to the parameter: κ1 = κ2 = κ3 = ...=μ.
- The binomial distributions, (number of successes in n independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
trials with probability p of success on each trial). The special case n = 1 is a Bernoulli distribution. Every cumulant is just n times the corresponding cumulant of the corresponding Bernoulli distribution. The derivative of the cumulant generating function is g '(t) = n·((p−1−1)·e−t + 1)−1. The first cumulants are κ1 = g '(0) = n·p and κ2 = g ' '(0) = κ1·(1−p). Substituting p = μ·n−1 gives g '(t) = ((μ−1 − n−1)·e−t + n−1)−1 and κ1 = μ. The limiting case n−1 = 0 is a Poisson distribution.
- The negative binomial distributionNegative binomial distributionIn probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
s, (number of failures before n successes with probability p of success on each trial). The special case n = 1 is a geometric distribution. Every cumulant is just n times the corresponding cumulant of the corresponding geometric distribution. The derivative of the cumulant generating function is g '(t) = n·((1−p)−1·e−t−1)−1. The first cumulants are κ1 = g '(0) = n·(p−1−1), and κ2 = g ' '(0) = κ1·p−1. Substituting p = (μ·n−1+1)−1 gives g '(t) = ((μ−1+n−1)·e−t−n−1)−1 and κ1 = μ. Comparing these formulas to those of the binomial distributions explains the name 'negative binomial distribution'. The limiting case n−1 = 0 is a Poisson distribution.
Introducing the variance-to-mean ratio
the above probability distributions get a unified formula for the derivative of the cumulant generating function:
The second derivative is
confirming that the first cumulant is κ1 = g '(0) = μ and the second cumulant is κ2 = g ' '(0) = μ·ε.
The constant random variables X = μ have є = 0. The binomial distributions have ε = 1 − p so that 0 < ε < 1. The Poisson distributions have ε = 1. The negative binomial distributions have ε = p−1 so that ε > 1. Note the analogy to the classification of conic sections by eccentricity
Eccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
: circles ε = 0, ellipses 0 < ε < 1, parabolas ε = 1, hyperbolas ε > 1.
Cumulants of some continuous probability distributions
- For the normal distribution with expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
μ and varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
σ2, the cumulant generating function is g(t) = μt + σ2t2/2. The first and second derivatives of the cumulant generating function are g '(t) = μ + σ2·t and g"(t) = σ2. The cumulants are κ1 = μ, κ2 = σ2, and κ3 = κ4 = ... = 0. The special case σ2 = 0 is a constant random variable X = μ.
- The cumulants of the uniform distributionUniform distribution (continuous)In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
on the interval [−1, 0] are κn = Bn/n, where Bn is the nth Bernoulli numberBernoulli numberIn mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
.
- The cumulants of the exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
with parameter λ are κn = λ−n (n − 1)!.
Some properties of the cumulant generating function
The cumulant generating function g(t) is convexConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
. If g(t) is finite for a range t1 < Re(t) < t2 then if t1 < 0 < t2 then g(t) is analytic and infinitely differentiable for t1 < Re(t) < t2. Moreover for t real and t1 < t < t2 g(t) is strictly convex, and g
Invariance and equivariance
The first cumulant is shift-equivariantEquivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
; all of the others are shift-invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
. This means that, if we denote by κn(X) the nth cumulant of the probability distribution of the random variable X, then for any constant c:
In other words, shifting a random variable (adding c) shifts the first cumulant (the mean) and doesn't affect any of the others.
Homogeneity
The nth cumulant is homogeneous of degree n, i.e. if c is any constant, then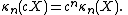Additivity
If X and Y are independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variables then κn(X + Y) = κn(X) + κn(Y).
A negative result
Given the results for the cumulants of the normal distribution, it might be hoped to find families of distributions for whichκm = κm+1 = ... = 0 for some m > 3, with the lower-order cumulants (orders 3 to m − 1) being non-zero. There are no such distributions. The underlying result here is that the cumulant generating function cannot be a finite-order polynomial of degree greater than 2.
Cumulants and moments
The moment generating function is: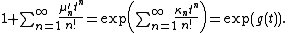So the cumulant generating function is the logarithm of the moment generating function.
The first cumulant is the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
; the second and third cumulants are respectively the second and third central moment
Central moment
In probability theory and statistics, central moments form one set of values by which the properties of a probability distribution can be usefully characterised...
s (the second central moment is the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
); but the higher cumulants are neither moments nor central moments, but rather more complicated polynomial functions of the moments.
The cumulants are related to the moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
by the following recursion
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
formula:
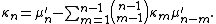
The nth moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
μ′n is an nth-degree polynomial in the first n cumulants:
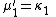
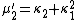
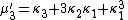
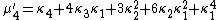
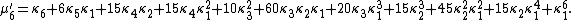
The coefficients are precisely those that occur in Faà di Bruno's formula
Faà di Bruno's formula
Faà di Bruno's formula is an identity in mathematics generalizing the chain rule to higher derivatives, named after , though he was not the first to state or prove the formula...
.
The "prime" distinguishes the moments μ′n from the central moments μn. To express the central moments as functions of the cumulants, just drop from these polynomials all terms in which κ1 appears as a factor:
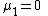
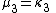
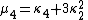
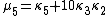
Likewise, the nth cumulant κn is an nth-degree polynomial in the first n non-central moments:
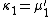
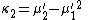
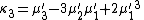
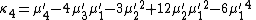
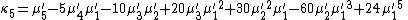
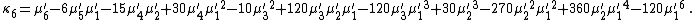
To express the cumulants κn for n > 1 as functions of the central moments, drop from these polynomials all terms in which μ'1 appears as a factor:
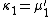
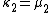
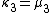
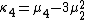
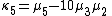
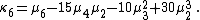
Cumulants and set-partitions
These polynomials have a remarkable combinatorialCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
interpretation: the coefficients count certain partitions of sets
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
. A general form of these polynomials is
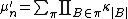
where
- π runs through the list of all partitions of a set of size n;
- "B
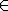π" means B is one of the "blocks" into which the set is partitioned; and
- |B| is the size of the set B.
Thus each monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
is a constant times a product of cumulants in which the sum of the indices is n (e.g., in the term κ3 κ22 κ1, the sum of the indices is 3 + 2 + 2 + 1 = 8; this appears in the polynomial that expresses the 8th moment as a function of the first eight cumulants). A partition of the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n corresponds to each term. The coefficient in each term is the number of partitions of a set of n members that collapse to that partition of the integer n when the members of the set become indistinguishable.
Joint cumulants
The joint cumulant of several random variables X1, ..., Xn is defined by a similar cumulant generating functionA consequence is that
where π runs through the list of all partitions of { 1, ..., n }, B runs through the list of all blocks of the partition π, and |π| is the number of parts in the partition. For example,
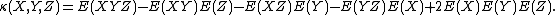
If any of these random variables are identical, e.g. if X = Y, then the same formulae apply, e.g.
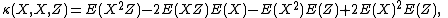
although for such repeated variables there are more concise formulae. For zero-mean random vectors,
The joint cumulant of just one random variable is its expected value, and that of two random variables is their covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
. If some of the random variables are independent of all of the others, then any cumulant involving two (or more) independent random variables is zero. If all n random variables are the same, then the joint cumulant is the nth ordinary cumulant.
The combinatorial meaning of the expression of moments in terms of cumulants is easier to understand than that of cumulants in terms of moments:
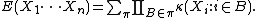
For example:
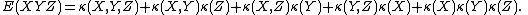
Another important property of joint cumulants is multilinearity:
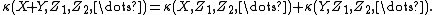
Just as the second cumulant is the variance, the joint cumulant of just two random variables is the covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
. The familiar identity
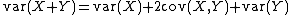
generalizes to cumulants:
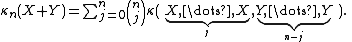
Conditional cumulants and the law of total cumulance
The law of total expectationLaw of total expectation
The proposition in probability theory known as the law of total expectation, the law of iterated expectations, the tower rule, the smoothing theorem, among other names, states that if X is an integrable random variable The proposition in probability theory known as the law of total expectation, ...
and the law of total variance
Law of total variance
In probability theory, the law of total variance or variance decomposition formula states that if X and Y are random variables on the same probability space, and the variance of Y is finite, then...
generalize naturally to conditional cumulants. The case n = 3, expressed in the language of (central) moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
rather than that of cumulants, says
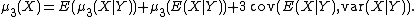
The general result stated below first appeared in 1969 in The Calculation of Cumulants via Conditioning by David R. Brillinger in volume 21 of Annals of the Institute of Statistical Mathematics, pages 215–218.
In general, we have
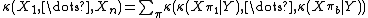
where
- the sum is over all partitionsPartition of a setIn mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
π of the set { 1, ..., n } of indices, and
- π1, ..., πb are all of the "blocks" of the partition π; the expression κ(Xπm) indicates that the joint cumulant of the random variables whose indices are in that block of the partition.
Relation to statistical physics
In statistical physicsStatistical physics
Statistical physics is the branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic...
many extensive quantities – that is quantities that are proportional to the volume or size of a given system – are related to cumulants of random variables. The deep connection is that in a large system an extensive quantity like the energy or number of particles can be thought of as the sum of (say) the energy associated with a number of nearly independent regions. The fact that the cumulants of these nearly independent random variables will (nearly) add make it reasonable that extensive quantities should be expected to be related to cumulants.
A system in equilibrium with a thermal bath at temperature T can occupy states of energy E. The energy E can be considered a random variable, having the probability density. The partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
of the system is
where β = 1/(kT) and k is Boltzmann's constant and the notation
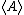has been used rather than 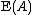for the expectation value to avoid confusion with the energy, E. The Helmholtz free energyHelmholtz free energy
In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...
is then
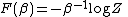
and is clearly very closely related to the cumulant generating function for the energy. The free energy gives access to all of the thermodynamics properties of the system via its first second and higher order derivatives, such as its internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
, entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
, and specific heat. Because of the relationship between the free energy and the cumulant generating function, all these quantities are related to cumulants e.g. the energy and specific heat are given by
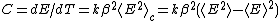
and
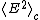symbolizes the second cumulant of the energy. Other free energy is often also a function of other variables such as the magnetic field or chemical potential 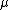, e.g.where N is the number of particles and
is the grand potential. Again the close relationship between the definition of the free energy and the cumulant generating function implies that various derivatives of this free energy can be written in terms of joint cumulants of E and N.History
The history of cumulants is discussed by Hald.Cumulants were first introduced by Thorvald N. Thiele
Thorvald N. Thiele
Thorvald Nicolai Thiele was a Danish astronomer, actuary and mathematician, most notable for his work in statistics, interpolation and the three-body problem. He was the first to propose a mathematical theory of Brownian motion...
, in 1889, who called them semi-invariants. They were first called cumulants in a 1932 paper by Ronald Fisher
Ronald Fisher
Sir Ronald Aylmer Fisher FRS was an English statistician, evolutionary biologist, eugenicist and geneticist. Among other things, Fisher is well known for his contributions to statistics by creating Fisher's exact test and Fisher's equation...
and John Wishart
John Wishart (statistician)
John Wishart was a Scottish mathematician and agricultural statistician.He worked successively at University College London with Karl Pearson, at Rothamsted Experimental Station with Ronald Fisher, and then as a reader in statistics in the University of Cambridge where he became the first...
. Fisher was publicly reminded of Thiele's work by Neyman, who also notes previous published citations of Thiele brought to Fisher's attention. Stephen Stigler
Stephen Stigler
Stephen Mack Stigler is Ernest DeWitt Burton Distinguished Service Professor at the Department of Statistics of the University of Chicago. His research has focused on statistical theory of robust estimators and the history of statistics...
has said that the name cumulant was suggested to Fisher in a letter from Harold Hotelling
Harold Hotelling
Harold Hotelling was a mathematical statistician and an influential economic theorist.He was Associate Professor of Mathematics at Stanford University from 1927 until 1931, a member of the faculty of Columbia University from 1931 until 1946, and a Professor of Mathematical Statistics at the...
. In a paper published in 1929, Fisher had called them cumulative moment functions. The partition function in statistical physics was introduced by Josiah Willard Gibbs
Josiah Willard Gibbs
Josiah Willard Gibbs was an American theoretical physicist, chemist, and mathematician. He devised much of the theoretical foundation for chemical thermodynamics as well as physical chemistry. As a mathematician, he invented vector analysis . Yale University awarded Gibbs the first American Ph.D...
in 1901. The free energy is often called Gibbs free energy. In statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, cumulants are also known as Ursell function
Ursell function
In statistical mechanics, an Ursell function or connected correlation function, is a cumulant ofa random variable. It is also called a connected correlation function as it can often be obtained by summing over...
s relating to a publication in 1927.
Formal cumulants
More generally, the cumulants of a sequence { mn : n = 1, 2, 3, ... }, not necessarily the moments of any probability distribution, are given by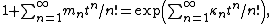where the values of κn for n = 1, 2, 3, ... are found formally, i.e., by algebra alone, in disregard of questions of whether any series converges. All of the difficulties of the "problem of cumulants" are absent when one works formally. The simplest example is that the second cumulant of a probability distribution must always be nonnegative, and is zero only if all of the higher cumulants are zero. Formal cumulants are subject to no such constraints.
Bell numbers
In combinatoricsCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, the nth Bell number
Bell number
In combinatorics, the nth Bell number, named after Eric Temple Bell, is the number of partitions of a set with n members, or equivalently, the number of equivalence relations on it...
is the number of partitions of a set of size n. All of the cumulants of the sequence of Bell numbers are equal to 1. The Bell numbers are the moments of the Poisson distribution with expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
1.
Cumulants of a polynomial sequence of binomial type
For any sequence { κn : n = 1, 2, 3, ... } of scalarsScalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
in a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of characteristic zero, being considered formal cumulants, there is a corresponding sequence { μ ′ : n = 1, 2, 3, ... } of formal moments, given by the polynomials above. For those polynomials, construct a polynomial sequence
Polynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
in the following way. Out of the polynomial
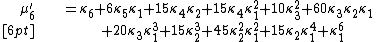
make a new polynomial in these plus one additional variable x:
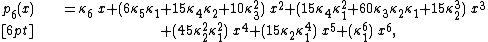
and then generalize the pattern. The pattern is that the numbers of blocks in the aforementioned partitions are the exponents on x. Each coefficient is a polynomial in the cumulants; these are the Bell polynomials, named after Eric Temple Bell
Eric Temple Bell
Eric Temple Bell , was a mathematician and science fiction author born in Scotland who lived in the U.S. for most of his life...
.
This sequence of polynomials is of binomial type. In fact, no other sequences of binomial type exist; every polynomial sequence of binomial type is completely determined by its sequence of formal cumulants.
Free cumulants
In the identity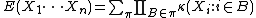one sums over all partitions of the set { 1, ..., n }. If instead, one sums only over the noncrossing partition
Noncrossing partition
In combinatorial mathematics, the topic of noncrossing partitions has assumed some importance because of its application to the theory of free probability...
s, then one gets "free cumulants" rather than conventional cumulants treated above. These play a central role in free probability
Free probability
Free probability is a mathematical theory that studies non-commutative random variables. The "freeness" or free independence property is the analogue of the classical notion of independence, and it is connected with free products....
theory. In that theory, rather than considering independence
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s, defined in terms of Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
s of algebras
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
of random variables, one considers instead "freeness" of random variables, defined in terms of free product
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
s of algebras rather than Cartesian products of algebras.
The ordinary cumulants of degree higher than 2 of the normal distribution are zero. The free cumulants of degree higher than 2 of the Wigner semicircle distribution are zero. This is one respect in which the role of the Wigner distribution in free probability theory is analogous to that of the normal distribution in conventional probability theory.
See also
- cumulant generating function from a multiset