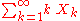
Geometric distribution
Encyclopedia
In probability theory
and statistics
, the geometric distribution is either of two discrete probability distributions:
one calls "the" geometric distribution is a matter of convention and convenience.
geometric distributions should not be confused with each other. Often, the name shifted geometric distribution is adopted for the former one (distribution of the number X); however, to avoid ambiguity, it is considered wise to indicate which is intended, by mentioning the range explicitly.
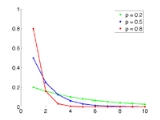
It’s the probability that the first occurrence of success require k number of independent trials, each with success probability p. If the probability of success on each trial is p, then the probability that the kth trial (out of k trials) is the first success is
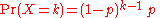
for k = 1, 2, 3, ....
The above form of Geometric Distribution is actually used for modeling number of trials until the first success.
Whereas the form of Geometric Distribution that is mentioned below is used for modeling number of failures until the first success.
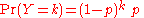
for k = 0, 1, 2, 3, ....
In either case, the sequence of probabilities is a geometric sequence.
For example, suppose an ordinary die
is thrown repeatedly until the first time a "1" appears. The probability distribution of the number of times it is thrown is supported on the infinite set { 1, 2, 3, ... } and is a geometric distribution with p = 1/6.
of a geometrically distributed random variable
X is 1/p and the variance
is (1 − p)/p2:

Similarly, the expected value of the geometrically distributed random variable Y is (1 − p)/p, and its variance is (1 − p)/p2:
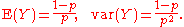
Let μ = (1 − p)/p be the expected value of Y. Then the cumulant
s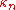 of the probability distribution of Y satisfy the recursion
of the probability distribution of Y satisfy the recursion

Outline of proof: That the expected value is (1 − p)/p can be shown in the following way. Let Y be as above. Then
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the geometric distribution is either of two discrete probability distributions:
- The probability distribution of the number X of Bernoulli trialBernoulli trialIn the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
s needed to get one success, supported on the set { 1, 2, 3, ...}
- The probability distribution of the number Y = X − 1 of failures before the first success, supported on the set { 0, 1, 2, 3, ... }
one calls "the" geometric distribution is a matter of convention and convenience.
geometric distributions should not be confused with each other. Often, the name shifted geometric distribution is adopted for the former one (distribution of the number X); however, to avoid ambiguity, it is considered wise to indicate which is intended, by mentioning the range explicitly.
It’s the probability that the first occurrence of success require k number of independent trials, each with success probability p. If the probability of success on each trial is p, then the probability that the kth trial (out of k trials) is the first success is
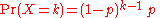
for k = 1, 2, 3, ....
The above form of Geometric Distribution is actually used for modeling number of trials until the first success.
Whereas the form of Geometric Distribution that is mentioned below is used for modeling number of failures until the first success.
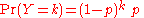
for k = 0, 1, 2, 3, ....
In either case, the sequence of probabilities is a geometric sequence.
For example, suppose an ordinary die
Dice
A die is a small throwable object with multiple resting positions, used for generating random numbers...
is thrown repeatedly until the first time a "1" appears. The probability distribution of the number of times it is thrown is supported on the infinite set { 1, 2, 3, ... } and is a geometric distribution with p = 1/6.
Moments and cumulants
The expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of a geometrically distributed random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X is 1/p and the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
is (1 − p)/p2:

Similarly, the expected value of the geometrically distributed random variable Y is (1 − p)/p, and its variance is (1 − p)/p2:
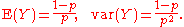
Let μ = (1 − p)/p be the expected value of Y. Then the cumulant
Cumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
s
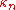 of the probability distribution of Y satisfy the recursion
of the probability distribution of Y satisfy the recursion
Outline of proof: That the expected value is (1 − p)/p can be shown in the following way. Let Y be as above. Then
-
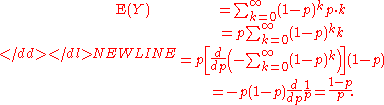
(The interchange of summation and differentiation is justified by the fact that convergent power series converge uniformly on compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
subsets of the set of points where they converge.)
Parameter estimation
For both variants of the geometric distribution, the parameter p can be estimated by equating the expected value with the sample mean. This is the method of moments, which in this case happens to yield maximum likelihoodMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimates of p.
Specifically, for the first variant let k = k1, ..., kn be a sampleSample (statistics)In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
where ki ≥ 1 for i = 1, ..., n. Then p can be estimated as
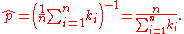
In Bayesian inferenceBayesian inferenceIn statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
, the Beta distribution is the conjugate priorConjugate priorIn Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
distribution for the parameter p. If this parameter is given a Beta(α, β) prior, then the posterior distribution is
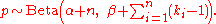
The posterior mean E[p] approaches the maximum likelihood estimate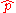 as α and β approach zero.
as α and β approach zero.
In the alternative case, let k1, ..., kn be a sample where ki ≥ 0 for i = 1, ..., n. Then p can be estimated as
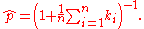
The posterior distribution of p given a Beta(α, β) prior is
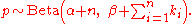
Again the posterior mean E[p] approaches the maximum likelihood estimate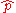 as α and β approach zero.
as α and β approach zero.
Other properties
- The probability-generating functionProbability-generating functionIn probability theory, the probability-generating function of a discrete random variable is a power series representation of the probability mass function of the random variable...
s of X and Y are, respectively,
-

- Like its continuous analogue (the exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
), the geometric distribution is memorylessMemorylessnessIn probability and statistics, memorylessness is a property of certain probability distributions: the exponential distributions of non-negative real numbers and the geometric distributions of non-negative integers....
. That means that if you intend to repeat an experiment until the first success, then, given that the first success has not yet occurred, the conditional probability distribution of the number of additional trials does not depend on how many failures have been observed. The die one throws or the coin one tosses does not have a "memory" of these failures. The geometric distribution is in fact the only memoryless discrete distribution.
- Among all discrete probability distributions supported on {1, 2, 3, ... } with given expected value μ, the geometric distribution X with parameter p = 1/μ is the one with the largest entropyMaximum entropy probability distributionIn statistics and information theory, a maximum entropy probability distribution is a probability distribution whose entropy is at least as great as that of all other members of a specified class of distributions....
.
- The geometric distribution of the number Y of failures before the first success is infinitely divisibleInfinite divisibility (probability)The concepts of infinite divisibility and the decomposition of distributions arise in probability and statistics in relation to seeking families of probability distributions that might be a natural choice in certain applications, in the same way that the normal distribution is...
, i.e., for any positive integer n, there exist independent identically distributed random variables Y1, ..., Yn whose sum has the same distribution that Y has. These will not be geometrically distributed unless n = 1; they follow a negative binomial distributionNegative binomial distributionIn probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
.
- The decimal digits of the geometrically distributed random variable Y are a sequence of independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
(and not identically distributed) random variables. For example, the hundreds digit D has this probability distribution:
-
- where q = 1 − p, and similarly for the other digits, and, more generally, similarly for numeral systemNumeral systemA numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
s with other bases than 10. When the base is 2, this shows that a geometrically distributed random variable can be written as a sum of independent random variables whose probability distributions are indecomposableIndecomposable distributionIn probability theory, an indecomposable distribution is a probability distribution that cannot be represented as the distribution of the sum of two or more non-constant independent random variables: Z ≠ X + Y. If it can be so expressed, it is decomposable:...
.
- Golomb codingGolomb codingGolomb coding is a lossless data compression method using a family of data compression codes invented by Solomon W. Golomb in the 1960s. Alphabets following a geometric distribution will have a Golomb code as an optimal prefix code, making Golomb coding highly suitable for situations in which the...
is the optimal prefix codePrefix codeA prefix code is a type of code system distinguished by its possession of the "prefix property"; which states that there is no valid code word in the system that is a prefix of any other valid code word in the set...
for the geometric discrete distribution.
Related distributions
- The geometric distribution Y is a special case of the negative binomial distributionNegative binomial distributionIn probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
, with r = 1. More generally, if Y1, ..., Yr are independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
geometrically distributed variables with parameter p, then the sum
- follows a negative binomial distribution with parameters r and '1-'p.
- If Y1, ..., Yr are independent geometrically distributed variables (with possibly different success parameters pm), then their minimum
- is also geometrically distributed, with parameter
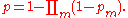
- Suppose 0 < r < 1, and for k = 1, 2, 3, ... the random variable Xk has a Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
with expected value r k/k. Then
- has a geometric distribution taking values in the set {0, 1, 2, ...}, with expected value r/(1 − r).
- The exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
is the continuous analogue of the geometric distribution. If X is an exponentially distributed random variable with parameter λ, then
- where
 is the floor (or greatest integer) function, is a geometrically distributed random variable with parameter p = 1 − e−λ (thus λ = −ln(1 − p)) and taking values in the set {0, 1, 2, ...}. This can be used to generate geometrically distributed pseudorandom numbers by first generating exponentially distributed pseudorandom numbers from a uniform pseudorandom number generatorPseudorandom number generatorA pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
is the floor (or greatest integer) function, is a geometrically distributed random variable with parameter p = 1 − e−λ (thus λ = −ln(1 − p)) and taking values in the set {0, 1, 2, ...}. This can be used to generate geometrically distributed pseudorandom numbers by first generating exponentially distributed pseudorandom numbers from a uniform pseudorandom number generatorPseudorandom number generatorA pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
: then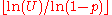 is geometrically distributed with parameter
is geometrically distributed with parameter 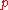 , if
, if  is uniformly distributed in [0,1].
is uniformly distributed in [0,1].
See also
- Hypergeometric distribution
- Coupon collector's problemCoupon collector's problemIn probability theory, the coupon collector's problem describes the "collect all coupons and win" contests. It asks the following question: Suppose that there are n coupons, from which coupons are being collected with replacement...
External links
- Geometric distribution on MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
. - Online geometric distribution calculator
- Like its continuous analogue (the exponential distribution
- The probability-generating function