Coefficient of variation
Encyclopedia
In probability theory
and statistics
, the coefficient of variation (CV) is a normalized
measure of dispersion
of a probability distribution
. It is also known as unitized risk or the variation coefficient. The absolute value of the CV is sometimes known as relative standard deviation
(RSD), which is expressed as a %. CV should not be used interchangeably with RSD (i.e. one term should be used consistently).
to the mean
:
which is the inverse of the signal-to-noise ratio
.
The coefficient of variation should be computed only for data measured on a ratio scale, which are measurements that can only take non-negative values. The coefficient of variation may not have any meaning for data on an interval scale.
For example, most temperature scales are interval scales (e.g. Celsius, Fahrenheit etc.), they can take both positive and negative values.
The Kelvin
scale has an absolute null value, and no negative values can naturally occur. Hence, the Kelvin scale is a ratio scale.
While the standard deviation (SD) can be derived on both the Kelvin and the Celsius scale (with both leading to the same SDs), the CV could only be derived for the Kelvin scale.
Often, laboratory values that are measured based on chromatographic methods are log-normally distributed.
In this case, the CV would be constant over a large range of measurements, while SDs would vary depending on the actual range that has been measured.
The CV is sometimes expressed as a percent, in which case the CV is multiplied by 100%.
Instead, the actual value of the CV is independent of the unit in which the measurement has been taken, so it is a dimensionless number.
For comparison between data sets with different units or widely different means, one should use the coefficient of variation instead of the standard deviation.
, queueing theory
, and reliability theory
. In these fields, the exponential distribution
is often more important than the normal distribution.
The standard deviation of an exponential distribution
is equal to its mean, so its coefficient of variation is equal to 1. Distributions with CV < 1 (such as an Erlang distribution) are considered low-variance, while those with CV > 1 (such as a hyper-exponential distribution) are considered high-variance. Some formulas in these fields are expressed using the squared coefficient of variation, often abbreviated SCV. In modeling, a variation of the CV is the CV(RMSD). Essentially the CV(RMSD) replaces the standard deviation term with the Root Mean Square Deviation (RMSD).
of the coefficient of variation for a sample of size n has been shown by Hendricks and Robey to be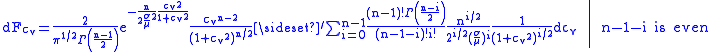
where the symbol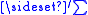
indicates that the summation is over only even values of n-1-i.
This is useful, for instance, in the construction of hypothesis tests or confidence interval
s.
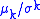, which are also dimensionless and scale invariant. The variance-to-mean ratio, 
, is another similar ratio, but is not dimensionless, and hence not scale invariant. See Normalization (statistics)
for further ratios.
In signal processing
, particularly image processing
, the reciprocal
ratio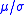
is referred to as the signal to noise ratio.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the coefficient of variation (CV) is a normalized
Normalization (statistics)
In one usage in statistics, normalization is the process of isolating statistical error in repeated measured data. A normalization is sometimes based on a property...
measure of dispersion
Statistical dispersion
In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...
of a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. It is also known as unitized risk or the variation coefficient. The absolute value of the CV is sometimes known as relative standard deviation
Relative standard deviation
In probability theory and statistics, the relative standard deviation is the absolute value of the coefficient of variation. It is often expressed as a percentage. A similar term that is sometimes used is the relative variance which is the square of the coefficient of variation...
(RSD), which is expressed as a %. CV should not be used interchangeably with RSD (i.e. one term should be used consistently).
Definition
The coefficient of variation (CV) is defined as the ratio of the standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
to the meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
:which is the inverse of the signal-to-noise ratio
Signal-to-noise ratio
Signal-to-noise ratio is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. It is defined as the ratio of signal power to the noise power. A ratio higher than 1:1 indicates more signal than noise...
.
The coefficient of variation should be computed only for data measured on a ratio scale, which are measurements that can only take non-negative values. The coefficient of variation may not have any meaning for data on an interval scale.
For example, most temperature scales are interval scales (e.g. Celsius, Fahrenheit etc.), they can take both positive and negative values.
The Kelvin
Kelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
scale has an absolute null value, and no negative values can naturally occur. Hence, the Kelvin scale is a ratio scale.
While the standard deviation (SD) can be derived on both the Kelvin and the Celsius scale (with both leading to the same SDs), the CV could only be derived for the Kelvin scale.
Often, laboratory values that are measured based on chromatographic methods are log-normally distributed.
In this case, the CV would be constant over a large range of measurements, while SDs would vary depending on the actual range that has been measured.
The CV is sometimes expressed as a percent, in which case the CV is multiplied by 100%.
Advantages
The coefficient of variation is useful because the standard deviation of data must always be understood in the context of the mean of the data.Instead, the actual value of the CV is independent of the unit in which the measurement has been taken, so it is a dimensionless number.
For comparison between data sets with different units or widely different means, one should use the coefficient of variation instead of the standard deviation.
Disadvantages
- When the mean value is close to zero, the coefficient of variation will approach infinity and is hence sensitive to small changes in the mean. This is often the case if the values do not originate from a ratio scale.
- Unlike the standard deviation, it cannot be used directly to construct confidence intervalConfidence intervalIn statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
s for the mean.
Applications
The coefficient of variation is also common in applied probability fields such as renewal theoryRenewal theory
Renewal theory is the branch of probability theory that generalizes Poisson processes for arbitrary holding times. Applications include calculating the expected time for a monkey who is randomly tapping at a keyboard to type the word Macbeth and comparing the long-term benefits of different...
, queueing theory
Queueing theory
Queueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
, and reliability theory
Reliability theory
Reliability theory describes the probability of a system completing its expected function during an interval of time. It is the basis of reliability engineering, which is an area of study focused on optimizing the reliability, or probability of successful functioning, of systems, such as airplanes,...
. In these fields, the exponential distribution
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
is often more important than the normal distribution.
The standard deviation of an exponential distribution
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
is equal to its mean, so its coefficient of variation is equal to 1. Distributions with CV < 1 (such as an Erlang distribution) are considered low-variance, while those with CV > 1 (such as a hyper-exponential distribution) are considered high-variance. Some formulas in these fields are expressed using the squared coefficient of variation, often abbreviated SCV. In modeling, a variation of the CV is the CV(RMSD). Essentially the CV(RMSD) replaces the standard deviation term with the Root Mean Square Deviation (RMSD).
Distribution
Provided that negative and small positive values of the sample mean occur with negligible frequency, the probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the coefficient of variation for a sample of size n has been shown by Hendricks and Robey to be
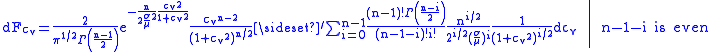
where the symbol
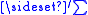indicates that the summation is over only even values of n-1-i.This is useful, for instance, in the construction of hypothesis tests or confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
s.
Similar ratios
Standardized moments are similar ratios,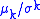, which are also dimensionless and scale invariant. The variance-to-mean ratio, , is another similar ratio, but is not dimensionless, and hence not scale invariant. See Normalization (statistics)Normalization (statistics)
In one usage in statistics, normalization is the process of isolating statistical error in repeated measured data. A normalization is sometimes based on a property...
for further ratios.
In signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, particularly image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
, the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
ratio
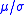is referred to as the signal to noise ratio.- Relative standard deviationRelative standard deviationIn probability theory and statistics, the relative standard deviation is the absolute value of the coefficient of variation. It is often expressed as a percentage. A similar term that is sometimes used is the relative variance which is the square of the coefficient of variation...
,
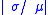
- Standardized moment,
- Variance-to-mean ratio,
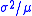
- Fano factor,
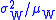(windowed VMR) - Signal-to-noise ratioSignal-to-noise ratioSignal-to-noise ratio is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. It is defined as the ratio of signal power to the noise power. A ratio higher than 1:1 indicates more signal than noise...
,
(in signal processingSignal processingSignal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
)- Signal-to-noise ratio (image processing)