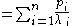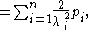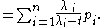Hyper-exponential distribution
Encyclopedia
In probability theory
, a hyper-exponential distribution is a continuous distribution such that the probability density function
of the random variable
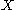is given by
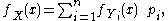
where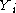
is an exponentially distributed
random variable with rate parameter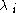
, and 
is the probability that X will take on the form of the exponential distribution with rate 
. It is named the hyper-exponential distribution since its coefficient of variation
is greater than that of the exponential distribution, whose coefficient of variation is 1, and the hypoexponential distribution
, which has a coefficient of variation less than one. While the exponential distribution
is the continuous analogue of the geometric distribution, the hyper-exponential distribution is not analogous to the hypergeometric distribution. The hyper-exponential distribution is an example of a mixture density
.
An example of a hyper-exponential random variable can be seen in the context of telephony
, where, if someone has a modem and a phone, their phone line usage could be modeled as a hyper-exponential distribution where there is probability p of them talking on the phone with rate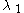
and probability q of them using their internet connection with rate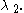 
and
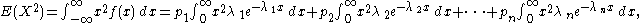
from which we can derive the variance.
The moment-generating function
is given by
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a hyper-exponential distribution is a continuous distribution such that the probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of the random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
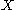is given by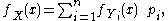where
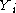is an exponentially distributedExponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
random variable with rate parameter
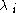, and is the probability that X will take on the form of the exponential distribution with rate . It is named the hyper-exponential distribution since its coefficient of variationCoefficient of variation
In probability theory and statistics, the coefficient of variation is a normalized measure of dispersion of a probability distribution. It is also known as unitized risk or the variation coefficient. The absolute value of the CV is sometimes known as relative standard deviation , which is...
is greater than that of the exponential distribution, whose coefficient of variation is 1, and the hypoexponential distribution
Hypoexponential distribution
In probability theory the hypoexponential distribution or the generalized Erlang distribution is a continuous distribution, that has found use in the same fields as the Erlang distribution, such as queueing theory, teletraffic engineering and more generally in stochastic processes...
, which has a coefficient of variation less than one. While the exponential distribution
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
is the continuous analogue of the geometric distribution, the hyper-exponential distribution is not analogous to the hypergeometric distribution. The hyper-exponential distribution is an example of a mixture density
Mixture density
In probability and statistics, a mixture distribution is the probability distribution of a random variable whose values can be interpreted as being derived in a simple way from an underlying set of other random variables. In particular, the final outcome value is selected at random from among the...
.
An example of a hyper-exponential random variable can be seen in the context of telephony
Telephony
In telecommunications, telephony encompasses the general use of equipment to provide communication over distances, specifically by connecting telephones to each other....
, where, if someone has a modem and a phone, their phone line usage could be modeled as a hyper-exponential distribution where there is probability p of them talking on the phone with rate
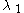and probability q of them using their internet connection with rate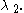 Properties of the hyper-exponential distribution
Since the expected value of a sum is the sum of the expected values, the expected value of a hyper-exponential random variable can be shown as
and
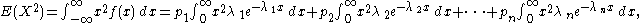
from which we can derive the variance.
The moment-generating function
Moment-generating function
In probability theory and statistics, the moment-generating function of any random variable is an alternative definition of its probability distribution. Thus, it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or...
is given by
See also
- phase-type distributionPhase-type distributionA phase-type distribution is a probability distribution that results from a system of one or more inter-related Poisson processes occurring in sequence, or phases. The sequence in which each of the phases occur may itself be a stochastic process. The distribution can be represented by a random...