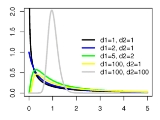
F-distribution
Encyclopedia
In probability theory
and statistics
, the F-distribution is a continuous probability distribution
. It is also known as Snedecor's F distribution or the Fisher-Snedecor distribution (after R.A. Fisher
and George W. Snedecor
). The F-distribution arises frequently as the null distribution
of a test statistic
, most notably in the analysis of variance
; see F-test
.
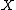 has an F-distribution with parameters
has an F-distribution with parameters 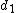 and
and 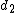 , we write
, we write 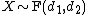 . Then the probability density function
. Then the probability density function
for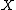 is given by
is given by
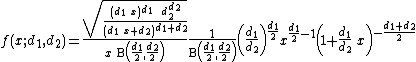
for real
 . Here
. Here 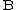 is the beta function. In many applications, the parameters
is the beta function. In many applications, the parameters 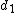 and
and 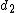 are positive integers, but the distribution is well-defined for positive real values of these parameters.
are positive integers, but the distribution is well-defined for positive real values of these parameters.
The cumulative distribution function
is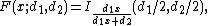
where I is the regularized incomplete beta function.
The expectation, variance, and other details about the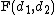 are given in the sidebox; for
are given in the sidebox; for 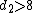 , the excess kurtosis is
, the excess kurtosis is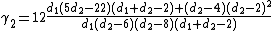 .
.
The k-th moment of an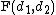 distribution exists and is finite only when
distribution exists and is finite only when 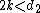 and it is equal to :
and it is equal to :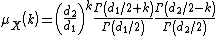
The F-distribution is a particular parametrization of the beta prime distribution, which is also called the beta distribution of the second kind.
The characteristic function
is listed incorrectly in many standard references (e.g.). The correct expression is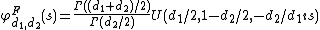
where is the confluent hypergeometric function
is the confluent hypergeometric function
of the second kind.
of the F-distribution with parameters d1 and d2 arises as the ratio of two appropriately scaled chi-squared variates:
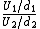
where
In instances where the F-distribution is used, for instance in the analysis of variance
, independence of U1 and U2 might be demonstrated by applying Cochran's theorem
.
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the F-distribution is a continuous probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. It is also known as Snedecor's F distribution or the Fisher-Snedecor distribution (after R.A. Fisher
Ronald Fisher
Sir Ronald Aylmer Fisher FRS was an English statistician, evolutionary biologist, eugenicist and geneticist. Among other things, Fisher is well known for his contributions to statistics by creating Fisher's exact test and Fisher's equation...
and George W. Snedecor
George W. Snedecor
George Waddel Snedecor was an American mathematician and statistician. He contributed to the foundations of analysis of variance, data analysis, experimental design, and statistical methodology. Snedecor's F distribution and the George W...
). The F-distribution arises frequently as the null distribution
Null distribution
In statistical hypothesis testing, the null distribution is the probability distribution of the test statistic when the null hypothesis is true.In an F-test, the null distribution is an F-distribution....
of a test statistic
Test statistic
In statistical hypothesis testing, a hypothesis test is typically specified in terms of a test statistic, which is a function of the sample; it is considered as a numerical summary of a set of data that...
, most notably in the analysis of variance
Analysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
; see F-test
F-test
An F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis.It is most often used when comparing statistical models that have been fit to a data set, in order to identify the model that best fits the population from which the data were sampled. ...
.
Definition
If a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
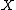 has an F-distribution with parameters
has an F-distribution with parameters 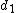 and
and 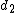 , we write
, we write 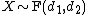 . Then the probability density function
. Then the probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
for
 is given by
is given by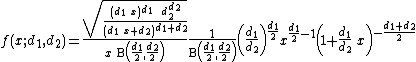
for real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
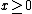 . Here
. Here 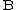 is the beta function. In many applications, the parameters
is the beta function. In many applications, the parameters 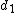 and
and 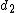 are positive integers, but the distribution is well-defined for positive real values of these parameters.
are positive integers, but the distribution is well-defined for positive real values of these parameters.The cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
is
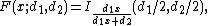
where I is the regularized incomplete beta function.
The expectation, variance, and other details about the
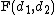 are given in the sidebox; for
are given in the sidebox; for 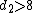 , the excess kurtosis is
, the excess kurtosis is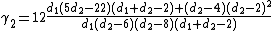 .
.The k-th moment of an
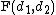 distribution exists and is finite only when
distribution exists and is finite only when 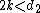 and it is equal to :
and it is equal to :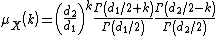
The F-distribution is a particular parametrization of the beta prime distribution, which is also called the beta distribution of the second kind.
The characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
is listed incorrectly in many standard references (e.g.). The correct expression is
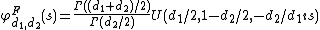
where
 is the confluent hypergeometric function
is the confluent hypergeometric functionConfluent hypergeometric function
In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity...
of the second kind.
Characterization
A random variateRandom variate
A random variate is a particular outcome of a random variable: the random variates which are other outcomes of the same random variable would have different values. Random variates are used when simulating processes driven by random influences...
of the F-distribution with parameters d1 and d2 arises as the ratio of two appropriately scaled chi-squared variates:
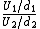
where
- U1 and U2 have chi-squared distributions with d1 and d2 degrees of freedomDegrees of freedom (statistics)In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
respectively, and
- U1 and U2 are independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
.
In instances where the F-distribution is used, for instance in the analysis of variance
Analysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
, independence of U1 and U2 might be demonstrated by applying Cochran's theorem
Cochran's theorem
In statistics, Cochran's theorem, devised by William G. Cochran, is a theorem used in to justify results relating to the probability distributions of statistics that are used in the analysis of variance.- Statement :...
.
Generalization
A generalization of the (central) F-distribution is the noncentral F-distributionNoncentral F-distribution
In probability theory and statistics, the noncentral F-distribution is a continuous probability distribution that is a generalization of the F-distribution...
.
Related distributions and properties
- If
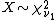 and
and 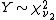 , and are independent, then
, and are independent, then 
- If
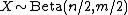 (Beta-distribution) then
(Beta-distribution) then 
- If
 then
then  has the chi-squared distribution
has the chi-squared distribution 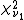
 is equivalent to the scaled Hotelling's T-squared distribution
is equivalent to the scaled Hotelling's T-squared distribution  .
.- If
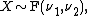 then
then 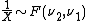 .
. - If
 (Student's t-distribution) then
(Student's t-distribution) then  .
. - If
 (Student's t-distribution) then
(Student's t-distribution) then  .
. - F-distribution is a special case of type 6 Pearson distributionPearson distributionThe Pearson distribution is a family of continuous probability distributions. It was first published by Karl Pearson in 1895 and subsequently extended by him in 1901 and 1916 in a series of articles on biostatistics.- History :...
- If
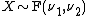 and
and 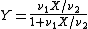 then
then  has a Beta-distribution.
has a Beta-distribution.
- If X and Y are independent, with
 and
and 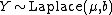 (Laplace distribution) then
(Laplace distribution) then
-
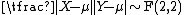
- If
 then
then  (Fisher's z-distribution)
(Fisher's z-distribution) - The noncentral F-distributionNoncentral F-distributionIn probability theory and statistics, the noncentral F-distribution is a continuous probability distribution that is a generalization of the F-distribution...
simplifies to the F-distribution if
- The doubly noncentral F-distributionNoncentral F-distributionIn probability theory and statistics, the noncentral F-distribution is a continuous probability distribution that is a generalization of the F-distribution...
simplifies to the F-distribution if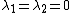
- If
- If
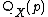 is the quantile
is the quantile 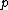 for
for 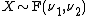 and
and 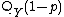 is the quantile
is the quantile 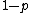 for
for  , then
, then
-
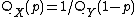 .
.

