A random variate is a particular outcome of a random variable

Random variable

In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...

: the random variates which are other outcomes of the same random variable would have different values. Random variates are used when simulating processes driven by random influences (stochastic processes). In modern applications, such simulations would derive random variates corresponding to any given probability distribution from computer procedures designed to create random variates corresponding to a uniform

Uniform distribution (continuous)

In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...

 distribution, where these procedures would actually provide values chosen from a uniform distribution

Uniform distribution (continuous)

In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...

 of pseudorandom numbers.

Procedures to generate random variates corresponding to a given distribution are known as procedures for random variate generation or pseudo-random number sampling

Pseudo-random number sampling

Pseudo-random number sampling or non-uniform pseudo-random variate generation is the numerical practice of generating pseudo-random numbers that are distributed according to a given probability distribution....

.

In probability theory

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

, a random variable

Random variable

In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...

 is a measurable function

Measurable function

In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...

 from a probability space

Probability space

In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...

 to a measurable space of values that the variable can take on. In that context, and in statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, those values are known as a random variates, or occasionally random deviates, and this represents a wider meaning than just that associated with pseudorandom numbers.

Definition

Devroye

Luc Devroye

Luc Devroye is a Belgian computer scientist and a James McGill Professor in the School of Computer Science of McGill University in Montreal, Canada. He studied at Katholieke Universiteit Leuven and subsequently at Osaka University and in 1976 received his PhD from University of Texas at Austin...

 defines a random variate generation algorithm (for real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s) as follows:

Assume that

1. Computers can manipulate real numbers.
2. Computers have access to a source of random variates that are uniformly distributed
   Uniform distribution (continuous)
   In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
   
    on the closed interval .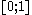

Then a random variate generation algorithm is any program that halts almost surely

Almost surely

In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...

 and exits with a real number X. This X is called a random variate.

(Both assumptions are violated in most real computers. Computers necessarily lack the ability to manipulate real numbers, typically using floating point

Floating point

In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...

 representations instead. Most computers lack a source of true randomness (like certain hardware random number generator

Hardware random number generator

In computing, a hardware random number generator is an apparatus that generates random numbers from a physical process. Such devices are often based on microscopic phenomena that generate a low-level, statistically random "noise" signal, such as thermal noise or the photoelectric effect or other...

s), and instead use pseudorandom number sequences.)

The distinction between random variable and random variate is subtle and is not always made in the literature. It is useful when one wants to distinguish between a random variable itself with an associated probability distribution

Probability distribution

In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....

 on the one hand, and random draws from that probability distribution on the other, in particular when those draws are ultimately derived by floating-point arithmetic from a pseudo-random sequence.

Practical aspects

For the generation of uniform random variates, see random number generation

Random number generation

A random number generator ) is a computational or physical device designed to generate a sequence of numbers or symbols that lack any pattern, i.e. appear random....

 (this is a bit of a misnomer, but a popular alternative to "random variate generation").

For the generation of non-uniform random variates, see pseudo-random number sampling

Pseudo-random number sampling

Pseudo-random number sampling or non-uniform pseudo-random variate generation is the numerical practice of generating pseudo-random numbers that are distributed according to a given probability distribution....

.