Beta function
Encyclopedia
In mathematics
, the beta function, also called the Euler integral of the first kind, is a special function defined by
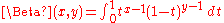
for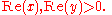
The beta function was studied by Euler
and Legendre
and was given its name by Jacques Binet
; its symbol Β is a Greek
capital β rather than the similar Latin
capital b
.
, meaning that
When x and y are positive integers, it follows trivially from the definition of the gamma function
that:
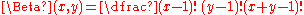
It has many other forms, including:
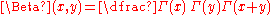
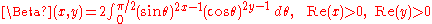
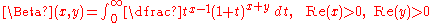
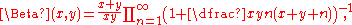
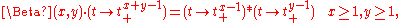
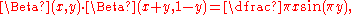
where
is a truncated power function and the star denotes convolution
.
The second identity shows in particular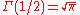
. Some of these identities, e.g. the trigonometric formula, can be applied to deriving the volume of an n-ball
in Cartesian coordinates.
Euler's integral for the beta function may be converted into an integral over the Pochhammer contour
C as
This Pochhammer contour integral converges for all values of α and β and so gives the analytic continuation
of the beta function.
Just as the gamma function for integers describes factorial
s, the beta function can define a binomial coefficient
after adjusting indices: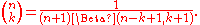
Moreover, for integer n,
can be integrated to give a closed form, an interpolation function for continuous values of k: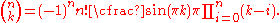
The beta function was the first known scattering amplitude
in string theory
, first conjectured by Gabriele Veneziano
. It also occurs in the theory of the preferential attachment
process, a type of stochastic urn process
.
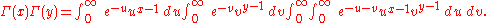
Changing variables by putting u=zt, v=z(1-t)
shows that this is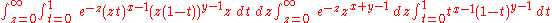
Hence
The stated identity may be seen as a particular case of the identity for the integral of a convolution. Taking
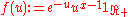and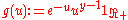 
, one has:
.
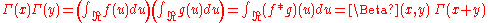where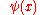
is the digamma function.
gives the asymptotic formula
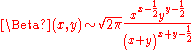
for large x and large y. If on the other hand x is large and y is fixed, then
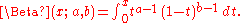
For x = 1, the incomplete beta function coincides with the complete beta function. The relationship between the two functions is like that between the gamma function and its generalization the incomplete gamma function
.
The regularized incomplete beta function (or regularized beta function for short) is defined in terms of the incomplete beta function and the complete beta function:
Working out the integral (one can use integration by parts
) for integer values of a and b, one finds:
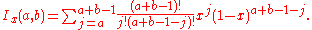
The regularized incomplete beta function is the cumulative distribution function
of the Beta distribution, and is related to the cumulative distribution function
of a random variable
X from a binomial distribution, where the "probability of success" is p and the sample size is n:
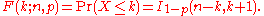
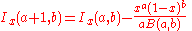
or Computer algebra system
s. With Excel
as an example, using the GammaLn and (cumulative
) Beta distribution functions, we have:
and,
These result from rearranging the formulae for the Beta distribution, and the incomplete beta and complete beta functions, which can also be defined as the ratio of the logs as above.
Similarly, in MATLAB
and GNU Octave
, betainc (Incomplete beta function) computes the regularized incomplete beta function - which is, in fact, the Cumulative Beta distribution - and so, to get the actual incomplete beta function, one must multiply the result of betainc by the result returned by the corresponding beta function.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the beta function, also called the Euler integral of the first kind, is a special function defined by
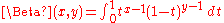
for
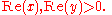
The beta function was studied by Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
and Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
and was given its name by Jacques Binet
Jacques Philippe Marie Binet
Jacques Philippe Marie Binet was a French mathematician, physicist and astronomer born in Rennes; he died in Paris, France, in 1856. He made significant contributions to number theory, and the mathematical foundations of matrix algebra which would later lead to important contributions by Cayley...
; its symbol Β is a Greek
Greek alphabet
The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
capital β rather than the similar Latin
Latin alphabet
The Latin alphabet, also called the Roman alphabet, is the most recognized alphabet used in the world today. It evolved from a western variety of the Greek alphabet called the Cumaean alphabet, which was adopted and modified by the Etruscans who ruled early Rome...
capital b
B
B is the second letter in the basic modern Latin alphabet. It is used to represent a variety of bilabial sounds , most commonly a voiced bilabial plosive.-History:...
.
Properties
The beta function is symmetricSymmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
, meaning that
When x and y are positive integers, it follows trivially from the definition of the gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
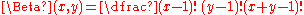
that:It has many other forms, including:
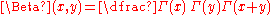
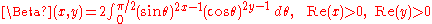
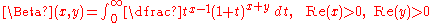
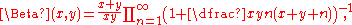
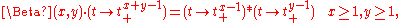
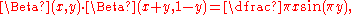
where
is a truncated power function and the star denotes convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
.
The second identity shows in particular
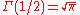. Some of these identities, e.g. the trigonometric formula, can be applied to deriving the volume of an n-ballDeriving the volume of an n-ball
In geometry, the volume of a sphere is a special case of the n-dimensional volume of a ball in n-dimensional Euclidean space.-Derivation of the volume of an n-ball:...
in Cartesian coordinates.
Euler's integral for the beta function may be converted into an integral over the Pochhammer contour
Pochhammer contour
In mathematics, the Pochhammer contour, introduced by and , is a contour in the complex plane with two points removed, used for contour integration...
C as
This Pochhammer contour integral converges for all values of α and β and so gives the analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of the beta function.
Just as the gamma function for integers describes factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
s, the beta function can define a binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
after adjusting indices:
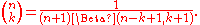
Moreover, for integer n,
can be integrated to give a closed form, an interpolation function for continuous values of k: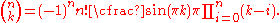The beta function was the first known scattering amplitude
S matrix
In physics, the scattering matrix relates the initial state and the final state of a physical system undergoing a scattering process...
in string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, first conjectured by Gabriele Veneziano
Gabriele Veneziano
Gabriele Veneziano, born in Florence, Italy), is an Italian theoretical physicist and the founder of string theory. . Has spent most of his scientific activities at CERN in Geneva, Switzerland...
. It also occurs in the theory of the preferential attachment
Preferential attachment
A preferential attachment process is any of a class of processes in which some quantity, typically some form of wealth or credit, is distributed among a number of individuals or objects according to how much they already have, so that those who are already wealthy receive more than those who are not...
process, a type of stochastic urn process
Urn problem
In probability and statistics, an urn problem is an idealized mental exercise in which some objects of real interest are represented as colored balls in an urn or other container....
.
Relationship between gamma function and beta function
To derive the integral representation of the beta function, write the product of two factorials as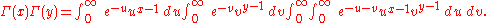Changing variables by putting u=zt, v=z(1-t)
shows that this is
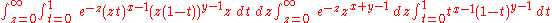
Hence
The stated identity may be seen as a particular case of the identity for the integral of a convolution. Taking
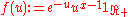and 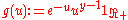, one has: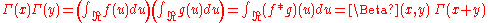.Derivatives
We havewhere
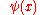is the digamma function.Approximation
Stirling's approximationStirling's approximation
In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
gives the asymptotic formula
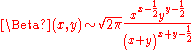
for large x and large y. If on the other hand x is large and y is fixed, then
Incomplete beta function
The incomplete beta function, a generalization of the beta function, is defined as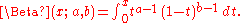For x = 1, the incomplete beta function coincides with the complete beta function. The relationship between the two functions is like that between the gamma function and its generalization the incomplete gamma function
Incomplete gamma function
In mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...
.
The regularized incomplete beta function (or regularized beta function for short) is defined in terms of the incomplete beta function and the complete beta function:
Working out the integral (one can use integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
) for integer values of a and b, one finds:
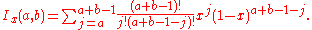
The regularized incomplete beta function is the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of the Beta distribution, and is related to the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X from a binomial distribution, where the "probability of success" is p and the sample size is n:
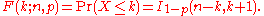
Properties
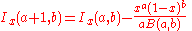
Calculation
Even if unavailable directly, the complete and incomplete Beta function values can be calculated using functions commonly included in spreadsheetSpreadsheet
A spreadsheet is a computer application that simulates a paper accounting worksheet. It displays multiple cells usually in a two-dimensional matrix or grid consisting of rows and columns. Each cell contains alphanumeric text, numeric values or formulas...
or Computer algebra system
Computer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
s. With Excel
Microsoft Excel
Microsoft Excel is a proprietary commercial spreadsheet application written and distributed by Microsoft for Microsoft Windows and Mac OS X. It features calculation, graphing tools, pivot tables, and a macro programming language called Visual Basic for Applications...
as an example, using the GammaLn and (cumulative
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
) Beta distribution functions, we have:
- Complete Beta Value = Exp(GammaLn(a) + GammaLn(b) - GammaLn(a + b))
and,
- Incomplete Beta Value = BetaDist(x, a, b) * Exp(GammaLn(a) + GammaLn(b) - GammaLn(a + b)).
These result from rearranging the formulae for the Beta distribution, and the incomplete beta and complete beta functions, which can also be defined as the ratio of the logs as above.
Similarly, in MATLAB
MATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
and GNU Octave
GNU Octave
GNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command-line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB...
, betainc (Incomplete beta function) computes the regularized incomplete beta function - which is, in fact, the Cumulative Beta distribution - and so, to get the actual incomplete beta function, one must multiply the result of betainc by the result returned by the corresponding beta function.
See also
- Beta distribution
- Binomial distribution
- Jacobi sumJacobi sumIn mathematics, a Jacobi sum is a type of character sum formed with Dirichlet characters. Simple examples would be Jacobi sums J for Dirichlet characters \chi, \psi modulo a prime number p, defined by...
, the analogue of the beta function over finite fields. - Negative binomial distributionNegative binomial distributionIn probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
- Yule–Simon distribution
- Uniform distribution (continuous)Uniform distribution (continuous)In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
- Gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
- Dirichlet distribution
External links
- Arbitrarily accurate values can be obtained from: