
Jacobi sum
Encyclopedia
In mathematics
, a Jacobi sum is a type of character sum
formed with Dirichlet character
s. Simple examples would be Jacobi sums J( ,
,  ) for Dirichlet characters
) for Dirichlet characters  ,
, 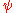 modulo a prime number p, defined by
modulo a prime number p, defined by
where the summation runs over all residues a = 2, 3, ..., p − 1 mod p (for which neither a nor 1 − a is 0). Jacobi sums are the analogues for finite fields of the beta function. Such sums were introduced by C. G. J. Jacobi early in the nineteenth century in connection with the theory of cyclotomy. Jacobi sums J can be factored generically into products of powers of Gauss sum
s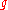 . For example, when the character
. For example, when the character  is nontrivial, J(
is nontrivial, J( ,
, 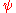 ) =
) = 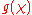
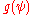 /
/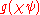 , analogous to the formula for the beta function in terms of gamma function
, analogous to the formula for the beta function in terms of gamma function
s. Since the nontrivial Gauss sums have absolute value p1/2, it follows that J(
have absolute value p1/2, it follows that J( ,
, 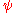 ) also has absolute value p1/2 when the characters
) also has absolute value p1/2 when the characters  ,
,  ,
, 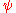 are nontrivial. Jacobi sums J lie in smaller cyclotomic field
are nontrivial. Jacobi sums J lie in smaller cyclotomic field
s than do the nontrivial Gauss sums . The summands of J(
. The summands of J( ,
, 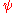 ) for example involve no p-th root of unity
) for example involve no p-th root of unity
, but rather involve just values which lie in the cyclotomic field of (p − 1)st roots of unity. Like Gauss sums, Jacobi sums have known prime ideal factorisations in their cyclotomic fields; see Stickelberger's theorem
.
When is the Legendre symbol
is the Legendre symbol
, J( ,
,  ) = −
) = − (−1) = (−1) (p+1)/2 . In general the values of Jacobi sums occur in relation with the local zeta-function
(−1) = (−1) (p+1)/2 . In general the values of Jacobi sums occur in relation with the local zeta-function
s of diagonal forms. The result on the Legendre symbol amounts to the formula p + 1 for the number of points on a conic section
that is a projective line
over the field of p elements. A paper of André Weil
from 1949 very much revived the subject. Indeed, through the Hasse-Davenport relation of the late 20th century, the formal properties of powers of Gauss sums had become current once more.
As well as pointing out the possibility of writing down local zeta-functions for diagonal hypersurfaces by means of general Jacobi sums, Weil (1952) demonstrated the properties of Jacobi sums as Hecke character
s. This was to become important once the complex multiplication of abelian varieties became established. The Hecke characters in question were exactly those one needs to express the Hasse-Weil L-functions of the Fermat curve
s, for example. The exact conductors of these characters, a question Weil had left open, were determined in later work.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Jacobi sum is a type of character sum
Character sum
In mathematics, a character sum is a sum\Sigma \chi\,of values of a Dirichlet character χ modulo N, taken over a given range of values of n. Such sums are basic in a number of questions, for example in the distribution of quadratic residues, and in particular in the classical question of finding an...
formed with Dirichlet character
Dirichlet character
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
s. Simple examples would be Jacobi sums J(
 ,
,  ) for Dirichlet characters
) for Dirichlet characters  ,
, 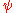 modulo a prime number p, defined by
modulo a prime number p, defined by- J(
 ,
, 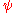 ) = Σ
) = Σ  (a)
(a)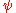 (1 − a),
(1 − a),
where the summation runs over all residues a = 2, 3, ..., p − 1 mod p (for which neither a nor 1 − a is 0). Jacobi sums are the analogues for finite fields of the beta function. Such sums were introduced by C. G. J. Jacobi early in the nineteenth century in connection with the theory of cyclotomy. Jacobi sums J can be factored generically into products of powers of Gauss sum
Gauss sum
In mathematics, a Gauss sum or Gaussian sum is a particular kind of finite sum of roots of unity, typicallyG := G= \sum \chi\cdot \psi...
s
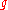 . For example, when the character
. For example, when the character  is nontrivial, J(
is nontrivial, J( ,
, 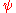 ) =
) = 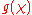
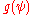 /
/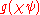 , analogous to the formula for the beta function in terms of gamma function
, analogous to the formula for the beta function in terms of gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
s. Since the nontrivial Gauss sums
 have absolute value p1/2, it follows that J(
have absolute value p1/2, it follows that J( ,
, 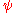 ) also has absolute value p1/2 when the characters
) also has absolute value p1/2 when the characters  ,
,  ,
, 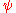 are nontrivial. Jacobi sums J lie in smaller cyclotomic field
are nontrivial. Jacobi sums J lie in smaller cyclotomic fieldCyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
s than do the nontrivial Gauss sums
 . The summands of J(
. The summands of J( ,
, 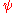 ) for example involve no p-th root of unity
) for example involve no p-th root of unityRoot of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
, but rather involve just values which lie in the cyclotomic field of (p − 1)st roots of unity. Like Gauss sums, Jacobi sums have known prime ideal factorisations in their cyclotomic fields; see Stickelberger's theorem
Stickelberger's theorem
In mathematics, Stickelberger's theorem is a result of algebraic number theory, which gives some information about the Galois module structure of class groups of cyclotomic fields...
.
When
 is the Legendre symbol
is the Legendre symbolLegendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
, J(
 ,
,  ) = −
) = − (−1) = (−1) (p+1)/2 . In general the values of Jacobi sums occur in relation with the local zeta-function
(−1) = (−1) (p+1)/2 . In general the values of Jacobi sums occur in relation with the local zeta-functionLocal zeta-function
In number theory, a local zeta-functionis a function whose logarithmic derivative is a generating functionfor the number of solutions of a set of equations defined over a finite field F, in extension fields Fk of F.-Formulation:...
s of diagonal forms. The result on the Legendre symbol amounts to the formula p + 1 for the number of points on a conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
that is a projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
over the field of p elements. A paper of André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
from 1949 very much revived the subject. Indeed, through the Hasse-Davenport relation of the late 20th century, the formal properties of powers of Gauss sums had become current once more.
As well as pointing out the possibility of writing down local zeta-functions for diagonal hypersurfaces by means of general Jacobi sums, Weil (1952) demonstrated the properties of Jacobi sums as Hecke character
Hecke character
In number theory, a Hecke character is a generalisation of a Dirichlet character, introduced by Erich Hecke to construct a class ofL-functions larger than Dirichlet L-functions, and a natural setting for the Dedekind zeta-functions and certain others which have functional equations analogous to...
s. This was to become important once the complex multiplication of abelian varieties became established. The Hecke characters in question were exactly those one needs to express the Hasse-Weil L-functions of the Fermat curve
Fermat curve
In mathematics, the Fermat curve is the algebraic curve in the complex projective plane defined in homogeneous coordinates by the Fermat equationX^n + Y^n = Z^n.\ Therefore in terms of the affine plane its equation is...
s, for example. The exact conductors of these characters, a question Weil had left open, were determined in later work.

