Diagonal form
Encyclopedia
In mathematics
, a diagonal form is an algebraic form (homogeneous polynomial
) without cross-terms involving different indeterminates
. That is, it is
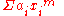
for some given degree m, summed for 1 ≤ i ≤ n.
Such forms F, and the hypersurface
s F = 0 they define in projective space
, are very special in geometric terms, with many symmetries. They also include famous cases like the Fermat curve
s, and other examples well known in the theory of Diophantine equation
s.
A great deal has been worked out about their theory: algebraic geometry
, local zeta-function
s via Jacobi sum
s, Hardy-Littlewood circle method
.
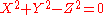is the unit circle
in P2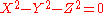
is the unit hyperbola
P2.
gives the Fermat cubic surface
in P3 with 27 lines. The 27 lines in this example are easy to describe explicitly: they are the 9 lines of the form (x : ax : y : by) where a and b are fixed numbers with cube −1, and their 18 conjugates under permutations of coordinates.
gives a K3 surface
in P3.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a diagonal form is an algebraic form (homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
) without cross-terms involving different indeterminates
Indeterminate (variable)
In mathematics, and particularly in formal algebra, an indeterminate is a symbol that does not stand for anything else but itself. In particular it does not designate a constant, or a parameter of the problem, it is not an unknown that could be solved for, it is not a variable designating a...
. That is, it is
for some given degree m, summed for 1 ≤ i ≤ n.
Such forms F, and the hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
s F = 0 they define in projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, are very special in geometric terms, with many symmetries. They also include famous cases like the Fermat curve
Fermat curve
In mathematics, the Fermat curve is the algebraic curve in the complex projective plane defined in homogeneous coordinates by the Fermat equationX^n + Y^n = Z^n.\ Therefore in terms of the affine plane its equation is...
s, and other examples well known in the theory of Diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
s.
A great deal has been worked out about their theory: algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, local zeta-function
Local zeta-function
In number theory, a local zeta-functionis a function whose logarithmic derivative is a generating functionfor the number of solutions of a set of equations defined over a finite field F, in extension fields Fk of F.-Formulation:...
s via Jacobi sum
Jacobi sum
In mathematics, a Jacobi sum is a type of character sum formed with Dirichlet characters. Simple examples would be Jacobi sums J for Dirichlet characters \chi, \psi modulo a prime number p, defined by...
s, Hardy-Littlewood circle method
Hardy-Littlewood circle method
In mathematics, the Hardy–Littlewood circle method is one of the most frequently used techniques of analytic number theory. It is named for G. H. Hardy and J. E...
.
Examples
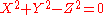is the unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
in P2
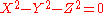is the unit hyperbolaUnit hyperbola
In geometry, the unit hyperbola is the set of points in the Cartesian plane that satisfies x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial lengthWhereas the unit circle surrounds its center, the unit hyperbola requires the...
P2.
gives the Fermat cubic surfaceCubic surface
A cubic surface is a projective variety studied in algebraic geometry. It is an algebraic surface in three-dimensional projective space defined by a single polynomial which is homogeneous of degree 3...
in P3 with 27 lines. The 27 lines in this example are easy to describe explicitly: they are the 9 lines of the form (x : ax : y : by) where a and b are fixed numbers with cube −1, and their 18 conjugates under permutations of coordinates.
gives a K3 surfaceK3 surface
In mathematics, a K3 surface is a complex or algebraic smooth minimal complete surface that is regular and has trivial canonical bundle.In the Enriques-Kodaira classification of surfaces they form one of the 5 classes of surfaces of Kodaira dimension 0....
in P3.