
Fermat curve
Encyclopedia
In mathematics
, the Fermat curve is the algebraic curve
in the complex projective plane defined in homogeneous coordinates
(X:Y:Z) by the Fermat equation

Therefore in terms of the affine plane its equation is
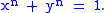
An integer solution to the Fermat equation would correspond to a nonzero rational number
solution to the affine equation, and vice versa. But by Fermat's last theorem
it is now known that (for n ≥ 3) there are no nontrivial integer solutions to the Fermat equation; therefore, the Fermat curve has no nontrivial rational points.
The Fermat curve is non-singular and has genus

This means genus 0 for the case n = 2 (a conic) and genus 1 only for n = 3 (an elliptic curve
). The Jacobian variety
of the Fermat curve has been studied in depth. It is isogenous to a product of simple abelian varieties with complex multiplication
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Fermat curve is the algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
in the complex projective plane defined in homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
(X:Y:Z) by the Fermat equation

Therefore in terms of the affine plane its equation is
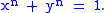
An integer solution to the Fermat equation would correspond to a nonzero rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
solution to the affine equation, and vice versa. But by Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
it is now known that (for n ≥ 3) there are no nontrivial integer solutions to the Fermat equation; therefore, the Fermat curve has no nontrivial rational points.
The Fermat curve is non-singular and has genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...

This means genus 0 for the case n = 2 (a conic) and genus 1 only for n = 3 (an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
). The Jacobian variety
Jacobian variety
In mathematics, the Jacobian variety J of a non-singular algebraic curve C of genus g is the moduli space of degree 0 line bundles...
of the Fermat curve has been studied in depth. It is isogenous to a product of simple abelian varieties with complex multiplication
Complex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
.

