Algebraic curve
Encyclopedia
In algebraic geometry
, an algebraic curve is an algebraic variety
of dimension
one. The theory of these curve
s in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circle
s and other conic section
s.
Using the resultant, we can eliminate all but two of the variables and reduce
the curve to a birationally equivalent
plane curve, f(x, y) = 0, still with coefficients in F, but usually of higher degree, and often possessing additional singularities. For example, eliminating z between the two equations x2 + y2 − z2 = 0 and x + 2y + 3z − 1 = 0, which defines an intersection of a cone and a plane in three dimensions, we obtain the conic section
8x2 + 5y2 − 4xy + 2x + 4y − 1 = 0, which in this case is an ellipse. If we eliminate z between 4x2 + y2 − z2 = 1 and z = x2, we obtain y2 = x4 − 4x2 + 1, which is the equation of a hyperelliptic curve.
. In the set of equations gi = 0, we can replace each xk with xk/x0, and multiply by x0n, where n is the degree of gi. In this way we obtain homogeneous
polynomial functions, which define the corresponding curve in projective space Pn. For a plane algebraic curve we have a single equation f(x, y, z) = 0, where f is homogeneous; for example, the Fermat curve
xn + yn - zn = 0 is a projective curve.
algebraic curves. Up to birational
equivalence, these are categorically equivalent
to algebraic function field
s. An algebraic function field is a field of algebraic functions in one variable K defined over a given field F. This means there exists an element x of K which is transcendental over F, and such that K is a finite algebraic extension of F(x), which is the field of rational functions in the indeterminate x over F.
For example, consider the field C of complex numbers, over which we may define the field C(x) of rational functions in C. If
y2 = x3 − x − 1, then the field C(x, y) is an elliptic function field
. The element x is not uniquely determined; the field can also be regarded, for instance, as an extension of C(y).
The algebraic curve corresponding to the function field is simply the set of
points (x, y) in C2 satisfying y2 = x3 − x − 1.
If the field F is not algebraically closed
, the point of view of function fields is a little more general than that of considering the locus of points, since we include, for instance, "curves" with no points on them. If the base field F is the field R of real numbers, then x2 + y2 = −1 defines an algebraic extension field of R(x), but the corresponding curve considered as a locus has no points in R. However, it does have points defined over the algebraic closure C of R.
, 2n, and is compact
, connected
, and orientable
. An algebraic curve likewise has topological dimension two; in other words, it is a surface. A nonsingular complex projective algebraic curve will then be a smooth orientable surface as a real manifold, embedded in a compact real manifold of dimension 2n which is CPn regarded as a real manifold. The topological genus of this surface, that is the number of handles or donut holes, is the genus of the curve. By considering the complex analytic structure induced on this compact surface we are led to the theory of compact Riemann surface
s.
if it is compact as a topological space.
There is a triple equivalence of categories between the category of smooth projective algebraic curves over the complex numbers, the category of compact Riemann surface
s, and the category of complex algebraic function fields, so that in studying these subjects we are in a sense studying the same thing. This allows complex analytic methods to be used in algebraic geometry, and algebraic-geometric methods in complex analysis, and field-theoretic methods to be used in both, which is characteristic of a much wider class of problems than simply curves and Riemann surfaces.
, points P on an algebraic curve C are classified as smooth or non-singular, or else singular
. Given n−1 homogeneous polynomial functions in
n+1 variables, we may find the Jacobian matrix as the (n−1)×(n+1) matrix
of partial derivatives. If the rank
of this matrix at a point P on the curve has the maximal value of n−1, then the point is a smooth point. In particular, if the curve is a plane projective algebraic curve, defined by a single homogeneous polynomial equation f(x,y,z) = 0, then the singular points are precisely the points P where the rank of the 1×(n+1) matrix is zero, that is, where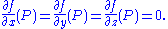
Since f is a polynomial, this definition is purely algebraic and makes no assumption about the nature of the field F, which in particular need not be the real or complex numbers. It should of course be recalled that (0,0,0) is not a point of the curve and hence not a singular point.
The singularities of a curve are not birational invariants. However, locating and classifying the singularities of a curve is one way of computing the genus
, which is a birational invariant. For this to work, we should consider the curve projectively and require F to be algebraically closed, so that all the singularities which belong to the curve are considered.
A curve C has at most a finite number of singular points. If it has none, it can be called smooth or non-singular. For this definition to be correct, we must use an algebraically closed field
and a curve C in projective space
(i.e., complete in the sense of algebraic geometry). If, for example, we simply look at a curve in the real affine plane there might be singular P modulo the stalk, or alternatively as the sum of m(m−1)/2, where m is the multiplicity, over all infinitely near singular points Q lying over the singular point P. Intuitively, a singular point with delta invariant δ concentrates δ ordinary double points at P. For an irreducible and reduced curve and a point P we can define δ algebraically as the length of
where 
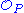is the local ring at P and 
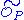is its integral closure. See also Hartshorne, Algebraic Geometry, IV Ex. 1.8.
The Milnor number
μ of the singularity is the degree of the mapping grad f(x,y)/|grad f(x,y)| on the small sphere of radius ε, in the sense of the topological degree of a continuous mapping
, where grad f is the (complex) gradient vector field of f. It is related to δ and r by the Milnor-Jung formula,
Another singularity invariant of note is the multiplicity m, defined as the maximum integer such that the derivatives of f to all orders up to m vanish.
Computing the delta invariants of all of the singularities allows the genus g of the curve to be determined; if d is the degree, then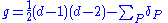
where the sum is taken over all singular points P of the complex projective plane curve.
Singularities may be classified by the triple [m, δ, r], where m is the multiplicity, δ is the delta-invariant, and r is the branching number. In these terms, an ordinary cusp is a point with invariants [2,1,1] and an ordinary double point is a point with invariants [2,1,2]. An ordinary n-multiple point may be defined as one having invariants [n, n(n−1)/2, n].
to a line, which we may take to be a projective line and identify with the field of rational functions in one indeterminate F(x). If F is algebraically closed, this is equivalent to a curve of genus
zero; however the
field R(x,y) with x2+y2 = −1 is a field of genus zero which is not a rational function field.
Concretely, a rational curve of dimension n over F can be parameterized (except for isolated exceptional points) by means of n rational functions defined in terms of a single parameter t; by clearing denominators we can turn this into
n+1 polynomial functions in projective space. An example would be the
rational normal curve.
Any conic section
defined over F with a rational point in F is a rational curve. It can be parameterized by drawing a line with slope t through the rational point, and intersection with the plane quadratic curve; this gives a polynomial with F-rational coefficients and one F-rational root, hence the other root is F-rational (i.e., belongs to F) also.
For example, consider the ellipse x2 + xy + y2 = 1, where (−1, 0) is a rational point. Drawing a line with slope t from (−1,0), y = t(x+1), substituting it in the equation of the ellipse, factoring, and solving for x, we obtain
We then have that the equation for y is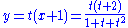
which defines a rational parameterization of the ellipse and hence shows the ellipse is a rational curve. All points of the ellipse are given, except for
(−1,1), which corresponds to t = ∞; the entire curve is parameterized therefore by the real projective line.
Viewing rational parameterizations with rational coefficients projectively, we can view them as giving number theoretical information about homogeneous equations defined over the integers. For example from the above, we obtain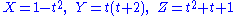
for which
is true for integer X, Y and Z if t is an integer. Hence
we obtain triangles with integer length sides, such as sides of length 3, 7, and 8, where one of the angles is 60°, from relationships such as 82−3·8+32 = 72.
Many of the curves on Wikipedia's list of curves are rational, and hence have similar rational parameterizations.
may be defined as any curve of genus
one with a rational point
: a common model is a nonsingular cubic curve
, which suffices to model any genus one curve. In this model the distinguished point is commonly taken to be an inflection point at infinity; this amounts to requiring that the curve can be written in Tate-Weierstrass form, which in its projective version is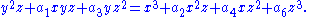
Elliptic curves carry the structure of an abelian group
with the distinguished point as the identity of the group law. In a plane cubic model three points sum to zero in the group if and only if they are collinear
. For an elliptic curve defined over the complex numbers the group is isomorphic to the additive group of the complex plane modulo the period lattice
of the corresponding elliptic function
s.
greater than one differ markedly from both rational and elliptic curves. Such curves defined over the rational numbers, by Faltings' theorem
, can have only a finite number of rational points, and they may be viewed as having a hyperbolic geometry
structure. Examples are the hyperelliptic curves, the Klein quartic curve
, and the Fermat curve
xn+yn = zn when n is greater than three.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, an algebraic curve is an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
of dimension
Dimension of an algebraic variety
In mathematics, the dimension of an algebraic variety V in algebraic geometry is defined, informally speaking, as the number of independent rational functions that exist on V.For example, an algebraic curve has by definition dimension 1...
one. The theory of these curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s and other conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s.
Plane algebraic curves
An algebraic curve defined over a field F may be considered as the locus of points in Fn determined by at least n − 1 independent polynomial functions in n variables with coefficients in F, gi(x1, …, xn), where the curve is defined by setting each gi = 0.Using the resultant, we can eliminate all but two of the variables and reduce
the curve to a birationally equivalent
Birational geometry
In mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...
plane curve, f(x, y) = 0, still with coefficients in F, but usually of higher degree, and often possessing additional singularities. For example, eliminating z between the two equations x2 + y2 − z2 = 0 and x + 2y + 3z − 1 = 0, which defines an intersection of a cone and a plane in three dimensions, we obtain the conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
8x2 + 5y2 − 4xy + 2x + 4y − 1 = 0, which in this case is an ellipse. If we eliminate z between 4x2 + y2 − z2 = 1 and z = x2, we obtain y2 = x4 − 4x2 + 1, which is the equation of a hyperelliptic curve.
Projective curves
It is often desirable to consider that curves are a locus of points in projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
. In the set of equations gi = 0, we can replace each xk with xk/x0, and multiply by x0n, where n is the degree of gi. In this way we obtain homogeneous
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
polynomial functions, which define the corresponding curve in projective space Pn. For a plane algebraic curve we have a single equation f(x, y, z) = 0, where f is homogeneous; for example, the Fermat curve
Fermat curve
In mathematics, the Fermat curve is the algebraic curve in the complex projective plane defined in homogeneous coordinates by the Fermat equationX^n + Y^n = Z^n.\ Therefore in terms of the affine plane its equation is...
xn + yn - zn = 0 is a projective curve.
Algebraic function fields
The study of algebraic curves can be reduced to the study of irreducibleIrreducible component
In mathematics, the concept of irreducible component is used to make formal the idea that a set such as defined by the equationis the union of the two linesandThe notion of irreducibility is stronger than connectedness.- Definition :...
algebraic curves. Up to birational
Birational geometry
In mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...
equivalence, these are categorically equivalent
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
to algebraic function field
Function field of an algebraic variety
In algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V...
s. An algebraic function field is a field of algebraic functions in one variable K defined over a given field F. This means there exists an element x of K which is transcendental over F, and such that K is a finite algebraic extension of F(x), which is the field of rational functions in the indeterminate x over F.
For example, consider the field C of complex numbers, over which we may define the field C(x) of rational functions in C. If
y2 = x3 − x − 1, then the field C(x, y) is an elliptic function field
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
. The element x is not uniquely determined; the field can also be regarded, for instance, as an extension of C(y).
The algebraic curve corresponding to the function field is simply the set of
points (x, y) in C2 satisfying y2 = x3 − x − 1.
If the field F is not algebraically closed
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
, the point of view of function fields is a little more general than that of considering the locus of points, since we include, for instance, "curves" with no points on them. If the base field F is the field R of real numbers, then x2 + y2 = −1 defines an algebraic extension field of R(x), but the corresponding curve considered as a locus has no points in R. However, it does have points defined over the algebraic closure C of R.
Complex curves and real surfaces
A complex projective algebraic curve resides in n-dimensional complex projective space CPn. This has complex dimension n, but topological dimension, as a real manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, 2n, and is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, and orientable
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
. An algebraic curve likewise has topological dimension two; in other words, it is a surface. A nonsingular complex projective algebraic curve will then be a smooth orientable surface as a real manifold, embedded in a compact real manifold of dimension 2n which is CPn regarded as a real manifold. The topological genus of this surface, that is the number of handles or donut holes, is the genus of the curve. By considering the complex analytic structure induced on this compact surface we are led to the theory of compact Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s.
Compact Riemann surfaces
A Riemann surface is a connected complex analytic manifold of one complex dimension, which makes it a connected real manifold of two dimensions. It is compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
if it is compact as a topological space.
There is a triple equivalence of categories between the category of smooth projective algebraic curves over the complex numbers, the category of compact Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s, and the category of complex algebraic function fields, so that in studying these subjects we are in a sense studying the same thing. This allows complex analytic methods to be used in algebraic geometry, and algebraic-geometric methods in complex analysis, and field-theoretic methods to be used in both, which is characteristic of a much wider class of problems than simply curves and Riemann surfaces.
Singularities
Using the intrinsic concept of tangent spaceTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
, points P on an algebraic curve C are classified as smooth or non-singular, or else singular
Singular point of a curve
In geometry, a singular point on a curve is one where the curve is not given by a smooth embedding of a parameter. The precise definition of a singular point depends on the type of curve being studied.-Algebraic curves in the plane:...
. Given n−1 homogeneous polynomial functions in
n+1 variables, we may find the Jacobian matrix as the (n−1)×(n+1) matrix
of partial derivatives. If the rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of this matrix at a point P on the curve has the maximal value of n−1, then the point is a smooth point. In particular, if the curve is a plane projective algebraic curve, defined by a single homogeneous polynomial equation f(x,y,z) = 0, then the singular points are precisely the points P where the rank of the 1×(n+1) matrix is zero, that is, where
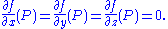
Since f is a polynomial, this definition is purely algebraic and makes no assumption about the nature of the field F, which in particular need not be the real or complex numbers. It should of course be recalled that (0,0,0) is not a point of the curve and hence not a singular point.
The singularities of a curve are not birational invariants. However, locating and classifying the singularities of a curve is one way of computing the genus
Geometric genus
In algebraic geometry, the geometric genus is a basic birational invariant pg of algebraic varieties and complex manifolds.-Definition:...
, which is a birational invariant. For this to work, we should consider the curve projectively and require F to be algebraically closed, so that all the singularities which belong to the curve are considered.
Classification of singularities
Singular points include multiple points where the curve crosses over itself, and also various types of cusp, for example that shown by the curve with equation x3 = y2 at (0,0).A curve C has at most a finite number of singular points. If it has none, it can be called smooth or non-singular. For this definition to be correct, we must use an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
and a curve C in projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
(i.e., complete in the sense of algebraic geometry). If, for example, we simply look at a curve in the real affine plane there might be singular P modulo the stalk, or alternatively as the sum of m(m−1)/2, where m is the multiplicity, over all infinitely near singular points Q lying over the singular point P. Intuitively, a singular point with delta invariant δ concentrates δ ordinary double points at P. For an irreducible and reduced curve and a point P we can define δ algebraically as the length of
where 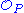is the local ring at P and 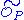is its integral closure. See also Hartshorne, Algebraic Geometry, IV Ex. 1.8.The Milnor number
Milnor number
In mathematics, and particularly singularity theory, the Milnor number, named after John Milnor, is an invariant of a function germ.If f is a complex-valued holomorphic function germ then the Milnor number of f, denoted μ, is either an integer greater than or equal to zero, or it is infinite. It...
μ of the singularity is the degree of the mapping grad f(x,y)/|grad f(x,y)| on the small sphere of radius ε, in the sense of the topological degree of a continuous mapping
Degree of a continuous mapping
In topology, the degree is a numerical invariant that describes a continuous mapping between two compact oriented manifolds of the same dimension. Intuitively, the degree represents the number of times that the domain manifold wraps around the range manifold under the mapping...
, where grad f is the (complex) gradient vector field of f. It is related to δ and r by the Milnor-Jung formula,
Another singularity invariant of note is the multiplicity m, defined as the maximum integer such that the derivatives of f to all orders up to m vanish.
Computing the delta invariants of all of the singularities allows the genus g of the curve to be determined; if d is the degree, then
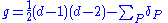
where the sum is taken over all singular points P of the complex projective plane curve.
Singularities may be classified by the triple [m, δ, r], where m is the multiplicity, δ is the delta-invariant, and r is the branching number. In these terms, an ordinary cusp is a point with invariants [2,1,1] and an ordinary double point is a point with invariants [2,1,2]. An ordinary n-multiple point may be defined as one having invariants [n, n(n−1)/2, n].
Rational curves
A rational curve, also called a unicursal curve, is any curve which is birationally equivalentBirational geometry
In mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...
to a line, which we may take to be a projective line and identify with the field of rational functions in one indeterminate F(x). If F is algebraically closed, this is equivalent to a curve of genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
zero; however the
field R(x,y) with x2+y2 = −1 is a field of genus zero which is not a rational function field.
Concretely, a rational curve of dimension n over F can be parameterized (except for isolated exceptional points) by means of n rational functions defined in terms of a single parameter t; by clearing denominators we can turn this into
n+1 polynomial functions in projective space. An example would be the
rational normal curve.
Any conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
defined over F with a rational point in F is a rational curve. It can be parameterized by drawing a line with slope t through the rational point, and intersection with the plane quadratic curve; this gives a polynomial with F-rational coefficients and one F-rational root, hence the other root is F-rational (i.e., belongs to F) also.
For example, consider the ellipse x2 + xy + y2 = 1, where (−1, 0) is a rational point. Drawing a line with slope t from (−1,0), y = t(x+1), substituting it in the equation of the ellipse, factoring, and solving for x, we obtain
We then have that the equation for y is
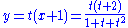
which defines a rational parameterization of the ellipse and hence shows the ellipse is a rational curve. All points of the ellipse are given, except for
(−1,1), which corresponds to t = ∞; the entire curve is parameterized therefore by the real projective line.
Viewing rational parameterizations with rational coefficients projectively, we can view them as giving number theoretical information about homogeneous equations defined over the integers. For example from the above, we obtain
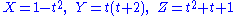
for which
is true for integer X, Y and Z if t is an integer. Hence
we obtain triangles with integer length sides, such as sides of length 3, 7, and 8, where one of the angles is 60°, from relationships such as 82−3·8+32 = 72.
Many of the curves on Wikipedia's list of curves are rational, and hence have similar rational parameterizations.
Elliptic curves
An elliptic curveElliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
may be defined as any curve of genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
one with a rational point
Rational point
In number theory, a K-rational point is a point on an algebraic variety where each coordinate of the point belongs to the field K. This means that, if the variety is given by a set of equationsthen the K-rational points are solutions ∈Kn of the equations...
: a common model is a nonsingular cubic curve
Cubic plane curve
In mathematics, a cubic plane curve is a plane algebraic curve C defined by a cubic equationapplied to homogeneous coordinates x:y:z for the projective plane; or the inhomogeneous version for the affine space determined by setting z = 1 in such an equation...
, which suffices to model any genus one curve. In this model the distinguished point is commonly taken to be an inflection point at infinity; this amounts to requiring that the curve can be written in Tate-Weierstrass form, which in its projective version is
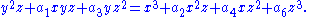
Elliptic curves carry the structure of an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
with the distinguished point as the identity of the group law. In a plane cubic model three points sum to zero in the group if and only if they are collinear
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
. For an elliptic curve defined over the complex numbers the group is isomorphic to the additive group of the complex plane modulo the period lattice
Fundamental pair of periods
In mathematics, a fundamental pair of periods is an ordered pair of complex numbers that define a lattice in the complex plane. This type of lattice is the underlying object with which elliptic functions and modular forms are defined....
of the corresponding elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s.
Curves of genus greater than one
Curves of genusGenus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
greater than one differ markedly from both rational and elliptic curves. Such curves defined over the rational numbers, by Faltings' theorem
Faltings' theorem
In number theory, the Mordell conjecture is the conjecture made by that a curve of genus greater than 1 over the field Q of rational numbers has only finitely many rational points. The conjecture was later generalized by replacing Q by a finite extension...
, can have only a finite number of rational points, and they may be viewed as having a hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
structure. Examples are the hyperelliptic curves, the Klein quartic curve
Klein quartic
In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
, and the Fermat curve
Fermat curve
In mathematics, the Fermat curve is the algebraic curve in the complex projective plane defined in homogeneous coordinates by the Fermat equationX^n + Y^n = Z^n.\ Therefore in terms of the affine plane its equation is...
xn+yn = zn when n is greater than three.