Equivalence of categories
Encyclopedia
In category theory
, an abstract branch of mathematics
, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics. Establishing an equivalence involves demonstrating strong similarities between the mathematical structures concerned. In some cases, these structures may appear to be unrelated at a superficial or intuitive level, making the notion fairly powerful: it creates the opportunity to "translate" theorems between different kinds of mathematical structures, knowing that the essential meaning of those theorems is preserved under the translation.
If a category is equivalent to the opposite (or dual)
of another category then one speaks of
a duality of categories, and says that the two categories are dually equivalent.
An equivalence of categories consists of a functor
between the involved categories, which is required to have an "inverse" functor. However, in contrast to the situation common for isomorphism
s in an algebraic setting, the composition of the functor and its "inverse" is not necessarily the identity mapping. Instead it is sufficient that each object be naturally isomorphic
to its image under this composition. Thus one may describe the functors as being "inverse up to isomorphism". There is indeed a concept of isomorphism of categories
where a strict form of inverse functor is required, but this is of much less practical use than the equivalence concept.
One often does not specify all the above data. For instance, we say that the categories C and D are equivalent (respectively dually equivalent) if there exists an equivalence (respectively duality) between them. Furthermore, we say that F "is" an equivalence of categories if an inverse functor G and natural isomorphisms as above exist. Note however that knowledge of F is usually not enough to reconstruct G and the natural isomorphisms: there may be many choices (see example below).
This is a quite useful and commonly applied criterion, because one does not have to explicitly construct the "inverse" G and the natural isomorphisms between FG, GF and the identity functors. On the other hand, though the above properties guarantee the existence of a categorical equivalence (given a sufficiently strong version of the axiom of choice in the underlying set theory), the missing data is not completely specified, and often there are many choices. It is a good idea to specify the missing constructions explicitly whenever possible.
Due to this circumstance, a functor with these properties is sometimes called a weak equivalence of categories (unfortunately this conflicts with terminology from homotopy theory).
There is also a close relation to the concept of adjoint functors
. The following statements are equivalent for functors F : C → D and G : D → C:
One may therefore view an adjointness relation between two functors as a "very weak form of equivalence". Assuming that the natural transformations for the adjunctions are given, all of these formulations allow for an explicit construction of the necessary data, and no choice principles are needed. The key property that one has to prove here is that the counit of an adjunction is an isomorphism if and only if the right adjoint is a full and faithful functor.
Dualities "turn all concepts around": they turn initial objects into terminal objects, monomorphisms into epimorphisms, kernels into cokernels, limits into colimits etc.
If F : C → D is an equivalence of categories, and G1 and G2 are two inverses, then G1 and G2 are naturally isomorphic.
If F : C → D is an equivalence of categories, and if C is a preadditive category
(or additive category
, or abelian category
), then D may be turned into a preadditive category (or additive category, or abelian category) in such a way that F becomes an additive functor. On the other hand, any equivalence between additive categories is necessarily additive. (Note that the latter statement is not true for equivalences between preadditive categories.)
An auto-equivalence of a category C is an equivalence F : C → C. The auto-equivalences of C form a group
under composition if we consider two auto-equivalences that are naturally isomorphic to be identical. This group captures the essential "symmetries" of C. (One caveat: if C is not a small category, then the auto-equivalences of C may form a proper class
rather than a set.)
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, an abstract branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics. Establishing an equivalence involves demonstrating strong similarities between the mathematical structures concerned. In some cases, these structures may appear to be unrelated at a superficial or intuitive level, making the notion fairly powerful: it creates the opportunity to "translate" theorems between different kinds of mathematical structures, knowing that the essential meaning of those theorems is preserved under the translation.
If a category is equivalent to the opposite (or dual)
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
of another category then one speaks of
a duality of categories, and says that the two categories are dually equivalent.
An equivalence of categories consists of a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
between the involved categories, which is required to have an "inverse" functor. However, in contrast to the situation common for isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
s in an algebraic setting, the composition of the functor and its "inverse" is not necessarily the identity mapping. Instead it is sufficient that each object be naturally isomorphic
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
to its image under this composition. Thus one may describe the functors as being "inverse up to isomorphism". There is indeed a concept of isomorphism of categories
Isomorphism of categories
In category theory, two categories C and D are isomorphic if there exist functors F : C → D and G : D → C which are mutually inverse to each other, i.e. FG = 1D and GF = 1C. This means that both the objects and the morphisms of C and D stand in a one to one correspondence to each other...
where a strict form of inverse functor is required, but this is of much less practical use than the equivalence concept.
Definition
Formally, given two categories C and D, an equivalence of categories consists of a functor F : C → D, a functor G : D → C, and two natural isomorphisms ε: FG→ID and η : IC→GF. Here FG: D→D and GF: C→C, denote the respective compositions of F and G, and IC: C→C and ID: D→D denote the identity functors on C and D, assigning each object and morphism to itself. If F and G are contravariant functors one speaks of a duality of categories instead.One often does not specify all the above data. For instance, we say that the categories C and D are equivalent (respectively dually equivalent) if there exists an equivalence (respectively duality) between them. Furthermore, we say that F "is" an equivalence of categories if an inverse functor G and natural isomorphisms as above exist. Note however that knowledge of F is usually not enough to reconstruct G and the natural isomorphisms: there may be many choices (see example below).
Equivalent characterizations
One can show that a functor F : C → D yields an equivalence of categories if and only if it is:- full, i.e. for any two objects c1 and c2 of C, the map HomC(c1,c2) → HomD(Fc1,Fc2) induced by F is surjective;
- faithful, i.e. for any two objects c1 and c2 of C, the map HomC(c1,c2) → HomD(Fc1,Fc2) induced by F is injective; and
- essentially surjective (dense)Essentially surjective functorIn category theory, a functorF:C\to Dis essentially surjective if each object d of D is isomorphic to an object of the form Fc for some object c of C. Any functor which is part of an equivalence is essentially surjective....
, i.e. each object d in D is isomorphic to an object of the form Fc, for c in C.
This is a quite useful and commonly applied criterion, because one does not have to explicitly construct the "inverse" G and the natural isomorphisms between FG, GF and the identity functors. On the other hand, though the above properties guarantee the existence of a categorical equivalence (given a sufficiently strong version of the axiom of choice in the underlying set theory), the missing data is not completely specified, and often there are many choices. It is a good idea to specify the missing constructions explicitly whenever possible.
Due to this circumstance, a functor with these properties is sometimes called a weak equivalence of categories (unfortunately this conflicts with terminology from homotopy theory).
There is also a close relation to the concept of adjoint functors
Adjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
. The following statements are equivalent for functors F : C → D and G : D → C:
- There are natural isomorphisms from FG to ID and IC to GF.
- F is a left adjoint of G and both functors are full and faithful.
- F is a right adjoint of G and both functors are full and faithful.
One may therefore view an adjointness relation between two functors as a "very weak form of equivalence". Assuming that the natural transformations for the adjunctions are given, all of these formulations allow for an explicit construction of the necessary data, and no choice principles are needed. The key property that one has to prove here is that the counit of an adjunction is an isomorphism if and only if the right adjoint is a full and faithful functor.
Examples
- Consider the category
having a single object 
and a single morphism 
, and the category 
with two objects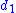 
, 
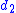and four morphisms: two identity morphisms 
, 
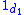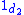and two isomorphisms 
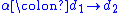and 
. The categories 
and 
are equivalent; we can (for example) have 
map 
to 
and 
map both objects of 
to 
and all morphisms to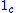 
.
- By contrast, the category
with a single object and a single morphism is not equivalent to the category 
with two objects and only two identity morphisms as the two objects therein are not isomorphic.
- Consider a category
with one object 
, and two morphisms 
. Let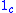 
be the identity morphism on 
and set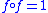 
. Of course, 
is equivalent to itself, which can be shown by taking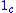 
in place of the required natural isomorphisms between the functor 
and itself. However, it is also true that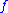 
yields a natural isomorphism from 
to itself. Hence, given the information that the identity functors form an equivalence of categories, in this example one still can choose between two natural isomorphisms for each direction.
- Consider the category
of finite-dimensional realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, and the category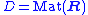
of all real matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
(the latter category is explained in the article on additive categoriesAdditive categoryIn mathematics, specifically in category theory, an additive category is a preadditive category C such that all finite collections of objects A1,...,An of C have a biproduct A1 ⊕ ⋯ ⊕ An in C....
). Then
and 
are equivalent: The functor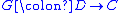 
which maps the object 
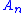of 
to the vector space 
and the matrices in 
to the corresponding linear maps is full, faithful and essentially surjective.
- One of the central themes of algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
is the duality of the category of affine schemes and the category of commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s. The functor
associates to every commutative ring its spectrumSpectrum of a ringIn abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
, the scheme defined by the prime idealPrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s of the ring. Its adjoint
associates to every affine scheme its ring of global sections.
- In functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
the category of commutative C*-algebras with identity is contravariantly equivalent to the category of compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s. Under this duality, every compact Hausdorff space
is associated with the algebra of continuous complex-valued functions on 
, and every commutative C*-algebra is associated with the space of its maximal idealMaximal idealIn mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
s. This is the Gelfand representationGelfand representationIn mathematics, the Gelfand representation in functional analysis has two related meanings:* a way of representing commutative Banach algebras as algebras of continuous functions;...
.
- In lattice theory, there are a number of dualities, based on representation theorems that connect certain classes of lattices to classes of topological spacesTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. Probably the most well-known theorem of this kind is Stone's representation theorem for Boolean algebrasStone's representation theorem for Boolean algebrasIn mathematics, Stone's representation theorem for Boolean algebras states that every Boolean algebra is isomorphic to a field of sets. The theorem is fundamental to the deeper understanding of Boolean algebra that emerged in the first half of the 20th century. The theorem was first proved by Stone...
, which is a special instance within the general scheme of Stone dualityStone dualityIn mathematics, there is an ample supply of categorical dualities between certain categories of topological spaces and categories of partially ordered sets. Today, these dualities are usually collected under the label Stone duality, since they form a natural generalization of Stone's representation...
. Each Boolean algebra
is mapped to a specific topology on the set of ultrafilters of 
. Conversely, for any topology the clopen (i.e. closed and open) subsets yield a Boolean algebra. One obtains a duality between the category of Boolean algebras (with their homomorphisms) and Stone spaces (with continuous mappings). Another case of Stone duality is Birkhoff's representation theoremBirkhoff's representation theoremIn mathematics, Birkhoff's representation theorem for distributive lattices states that the elements of any finite distributive lattice can be represented as finite sets, in such a way that the lattice operations correspond to unions and intersections of sets...
stating a duality between finite partial orders and finite distributive lattices.
- In pointless topologyPointless topologyIn mathematics, pointless topology is an approach to topology that avoids mentioning points. The name 'pointless topology' is due to John von Neumann...
the category of spatial locales is known to be equivalent to the dual of the category of sober spaces.
- Any category is equivalent to its skeletonSkeleton (category theory)In mathematics, a skeleton of a category is a subcategory which, roughly speaking, does not contain any extraneous isomorphisms. In a certain sense, the skeleton of a category is the "smallest" equivalent category which captures all "categorical properties". In fact, two categories are equivalent...
.
Properties
As a rule of thumb, an equivalence of categories preserves all "categorical" concepts and properties. If F : C → D is an equivalence, then the following statements are all true:- the object c of C is an initial objectInitial objectIn category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
(or terminal object, or zero object), if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
Fc is an initial objectInitial objectIn category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
(or terminal object, or zero object) of D - the morphism α in C is a monomorphismMonomorphismIn the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
(or epimorphismEpimorphismIn category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
, or isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
), if and only if Fα is a monomorphism (or epimorphism, or isomorphism) in D. - the functor H : I → C has limitLimit (category theory)In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
(or colimit) l if and only if the functor FH : I → D has limit (or colimit) Fl. This can be applied to equalizers, productProduct (category theory)In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
s and coproductCoproductIn category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
s among others. Applying it to kernelKernel (category theory)In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
s and cokernelCokernelIn mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
s, we see that the equivalence F is an exact functor. - C is a cartesian closed categoryCartesian closed categoryIn category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
(or a toposToposIn mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
) if and only if D is cartesian closed (or a topos).
Dualities "turn all concepts around": they turn initial objects into terminal objects, monomorphisms into epimorphisms, kernels into cokernels, limits into colimits etc.
If F : C → D is an equivalence of categories, and G1 and G2 are two inverses, then G1 and G2 are naturally isomorphic.
If F : C → D is an equivalence of categories, and if C is a preadditive category
Preadditive category
In mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
(or additive category
Additive category
In mathematics, specifically in category theory, an additive category is a preadditive category C such that all finite collections of objects A1,...,An of C have a biproduct A1 ⊕ ⋯ ⊕ An in C....
, or abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
), then D may be turned into a preadditive category (or additive category, or abelian category) in such a way that F becomes an additive functor. On the other hand, any equivalence between additive categories is necessarily additive. (Note that the latter statement is not true for equivalences between preadditive categories.)
An auto-equivalence of a category C is an equivalence F : C → C. The auto-equivalences of C form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under composition if we consider two auto-equivalences that are naturally isomorphic to be identical. This group captures the essential "symmetries" of C. (One caveat: if C is not a small category, then the auto-equivalences of C may form a proper class
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
rather than a set.)