Gelfand representation
Encyclopedia
In mathematics
, the Gelfand representation in functional analysis
(named after I. M. Gelfand) has two related meanings:
In the former case, one may regard the Gelfand representation as a far-reaching generalization of the Fourier transform
of an integrable function. In the latter case, the Gelfand-Naimark representation theorem is one avenue in the development of spectral theory
for normal operator
s, and generalizes the notion of diagonalizing a normal matrix.
(see the citation below), characterizing the elements of the group algebra
s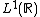
and 
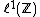whose translates span dense subspaces in the respective algebras.
Hausdorff
topological space
X, the space C0(X) of continuous complex-valued functions on X which vanish at infinity is in a natural way a commutative C*-algebra:
Note that A is unital if and only if X is compact
, in which case C0(X) is equal to C(X), the algebra of all continuous complex-valued functions on X.
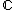of complex numbers.
A non-zero algebra homomorphism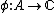
is called a character of 
; the set of all characters of A is denoted by 
.
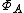It can be shown that every character on A is automatically continuous, and hence
is a subset of the space 
of continuous linear functionals on A; moreover, when equipped with the relative weak-* topology,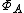 
turns out to be locally compact and Hausdorff. (This follows from the Banach-Alaoglu theorem
.)
The space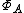
is compact (in the topology just defined) if and only if the algebra A has an identity element.
Given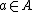
, one defines the function 
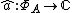by 
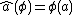. The definition of 
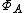and the topology on it ensure that 
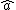is continuous and vanishes at infinity, and that the map 
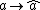defines a norm-decreasing, unit-preserving algebra homomorphism from A to 
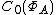. This homomorphism is the Gelfand representation of A, and 
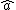is the Gelfand transform of the element 
. In general the representation is neither injective nor surjective.
In the case where A has an identity element, there is a bijection between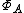
and the set of maximal proper ideals in A (this relies on the Gelfand-Mazur theorem
). As a consequence, the kernel of the Gelfand representation
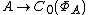may be identified with the Jacobson radical
of A. Thus the Gelfand representation is injective if and only if A is (Jacobson) semisimple
.
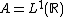, the group algebra 
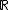, then 
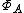is homeomorphic to 
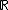and the Gelfand transform of 
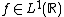is the Fourier transform
.
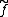In the case where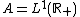
, the L1-convolution algebra of the real half-line, then 
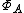is homeomorphic to 
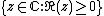, and the Gelfand transform of an element 
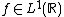is the Laplace transform 
.
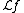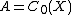. Given x in X, let 
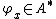be pointwise evaluation at x, i.e. 
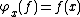. Then 
is a character on 
, and it can be shown that all characters of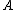 
are of this form; a more precise analysis shows that we may identify 
with X, not just as sets but as topological spaces. The Gelfand representation is then an isomorphism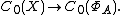
(It can be shown that every algebra homomorphism from A to the complex numbers is automatically a *-homomorphism, so that this definition of the term 'character' agrees with the one above.)
In particular, the spectrum of a commutative C*-algebra is a locally compact Hausdorff space: In the unital case, i.e. where the C*-algebra has a multiplicative unit element 1, all characters f must be unital, i.e. f(1) is the complex number one. This excludes the zero homomorphism. So  is closed under weak-* convergence and the spectrum is actually compact. In the non-unital case, the weak-* closure of  is  ∪ {0}, where 0 is the zero homomorphism, and the removal of a single point from a compact Hausdorff space yields a locally compact Hausdorff space.
Note that spectrum is an overloaded word. It also refers to the spectrum σ(x) of an element x of an algebra with unit 1, that is the set of complex numbers r for which x - r 1 is not invertible in A. For unital C*-algebras, the two notions are connected in the following way: σ(x) is the set of complex numbers f(x) where f ranges over Gelfand space of A. Together with the spectral radius formula
, this shows that  is a subset of the unit ball of A* and as such can be given the relative weak-* topology. This is the topology of pointwise convergence. A net
{fk}k of elements of the spectrum of A converges to f if and only if
for each x in A, the net of complex numbers {fk(x)}k converges to f(x).
If A is a separable C*-algebra, the weak-* topology is metrizable on bounded subsets. Thus the spectrum of a separable commutative C*-algebra A can be regarded as a metric space. So the topology can be characterized via convergence of sequences.
Equivalently, σ(x) is the range
of γ(x), where γ is the Gelfand representation.
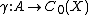
be the Gelfand representation defined above.
Theorem. The Gelfand map γ is an isometric *-isomorphism from A onto C0(X).
See the Arveson reference below.
The spectrum of a commutative C*-algebra can also be viewed as the set of all maximal ideal
s m of A, with the hull-kernel topology. (See the earlier remarks for the general, commutative Banach algebra case.) For any such m the quotient algebra A/m is one-dimensional (by the Gelfand-Mazur theorem), and therefore any a in A gives rise to a complex-valued function on Y.
In the case of C*-algebras with unit, the spectrum map gives rise to a contravariant functor
from the category of C*-algebras with unit and unit-preserving continuous *-homomorphisms, to the category of compact Hausdorff spaces and continuous maps. This functor is one half of a contravariant equivalence
between these two categories (its adjoint being the functor that assigns to each compact Hausdorff space X the C*-algebra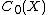
). In particular, given compact Hausdorff spaces X and Y, then C(X) is isomorphic to C(Y) (as a C*-algebra) if and only if X is homeomorphic to Y.
The 'full' Gelfand–Naimark theorem
is a result for arbitrary (abstract) noncommutative C*-algebras A, which though not quite analogous to the Gelfand representation, does provide a concrete representation of A as an algebra of operators.
Theorem. Let A be a C*-algebra with identity and x an element of A. Then there is a *-morphism f → f(x) from the algebra of continuous functions on the spectrum σ(x) into A such that
This allows us to apply continuous functions to bounded normal operators on Hilbert space.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Gelfand representation in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
(named after I. M. Gelfand) has two related meanings:
- a way of representing commutative Banach algebraBanach algebraIn mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
s as algebras of continuous functions; - the fact that for commutative C*-algebras, this representation is an isometric isomorphism.
In the former case, one may regard the Gelfand representation as a far-reaching generalization of the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of an integrable function. In the latter case, the Gelfand-Naimark representation theorem is one avenue in the development of spectral theory
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
for normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
s, and generalizes the notion of diagonalizing a normal matrix.
Historical remarks
One of Gelfand's original applications (and one which historically motivated much of the study of Banach algebras) was to give a much shorter and more conceptual proof of a celebrated lemma of Norbert WienerNorbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
(see the citation below), characterizing the elements of the group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
s
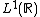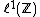and whose translates span dense subspaces in the respective algebras.The model algebra
For any locally compactLocally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X, the space C0(X) of continuous complex-valued functions on X which vanish at infinity is in a natural way a commutative C*-algebra:
- The structure of algebra over the complex numbers is obtained by considering the pointwise operations of addition and multiplication.
- The involution is pointwise complex conjugation.
- The norm is the uniform norm on functions.
Note that A is unital if and only if X is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, in which case C0(X) is equal to C(X), the algebra of all continuous complex-valued functions on X.
The Gelfand representation of a commutative Banach algebra
Let A be a commutative Banach algebra, defined over the field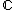 of complex numbers.A non-zero algebra homomorphism
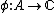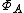is called a character of ; the set of all characters of A is denoted by .It can be shown that every character on A is automatically continuous, and hence
is a subset of the space of continuous linear functionals on A; moreover, when equipped with the relative weak-* topology, 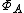turns out to be locally compact and Hausdorff. (This follows from the Banach-Alaoglu theoremBanach-Alaoglu theorem
In functional analysis and related branches of mathematics, the Banach–Alaoglu theorem states that the closed unit ball of the dual space of a normed vector space is compact in the weak* topology. A common proof identifies the unit ball with the weak* topology as a closed subset of a product of...
.)
The space
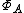is compact (in the topology just defined) if and only if the algebra A has an identity element.Given
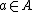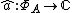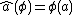, one defines the function by . The definition of 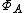and the topology on it ensure that 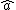is continuous and vanishes at infinity, and that the map 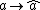defines a norm-decreasing, unit-preserving algebra homomorphism from A to 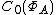. This homomorphism is the Gelfand representation of A, and 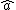is the Gelfand transform of the element . In general the representation is neither injective nor surjective.In the case where A has an identity element, there is a bijection between
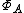and the set of maximal proper ideals in A (this relies on the Gelfand-Mazur theoremGelfand-Mazur theorem
In operator theory, the Gelfand–Mazur theorem is a theorem named after Israel Gelfand and Stanisław Mazur which states:In other words, the only complex Banach algebra that is a division algebra is the complex numbers C...
). As a consequence, the kernel of the Gelfand representation
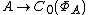may be identified with the Jacobson radicalJacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
of A. Thus the Gelfand representation is injective if and only if A is (Jacobson) semisimple
Semiprimitive ring
In mathematics, especially in the area of algebra known as ring theory, a semiprimitive ring is a type of ring more general than a semisimple ring, but where simple modules still provide enough information about the ring. Important rings such as the ring of integers are semiprimitive, and an...
.
Examples
In the case where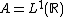, the group algebra 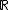, then 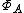is homeomorphic to 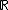and the Gelfand transform of 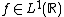is the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
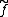.In the case where
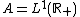, the L1-convolution algebra of the real half-line, then 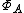is homeomorphic to 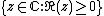, and the Gelfand transform of an element 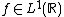is the Laplace transform 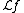.The C*-algebra case
As motivation, consider the special case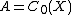. Given x in X, let 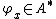be pointwise evaluation at x, i.e. 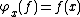. Then is a character on , and it can be shown that all characters of 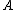are of this form; a more precise analysis shows that we may identify with X, not just as sets but as topological spaces. The Gelfand representation is then an isomorphism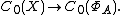The spectrum of a commutative C*-algebra
The spectrum or Gelfand space of a commutative C*-algebra A, denoted Â, consists of the set of non-zero *-homomorphisms from A to the complex numbers. Elements of the spectrum are called characters on A.(It can be shown that every algebra homomorphism from A to the complex numbers is automatically a *-homomorphism, so that this definition of the term 'character' agrees with the one above.)
In particular, the spectrum of a commutative C*-algebra is a locally compact Hausdorff space: In the unital case, i.e. where the C*-algebra has a multiplicative unit element 1, all characters f must be unital, i.e. f(1) is the complex number one. This excludes the zero homomorphism. So  is closed under weak-* convergence and the spectrum is actually compact. In the non-unital case, the weak-* closure of  is  ∪ {0}, where 0 is the zero homomorphism, and the removal of a single point from a compact Hausdorff space yields a locally compact Hausdorff space.
Note that spectrum is an overloaded word. It also refers to the spectrum σ(x) of an element x of an algebra with unit 1, that is the set of complex numbers r for which x - r 1 is not invertible in A. For unital C*-algebras, the two notions are connected in the following way: σ(x) is the set of complex numbers f(x) where f ranges over Gelfand space of A. Together with the spectral radius formula
Spectral radius
In mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
, this shows that  is a subset of the unit ball of A* and as such can be given the relative weak-* topology. This is the topology of pointwise convergence. A net
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
{fk}k of elements of the spectrum of A converges to f if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
for each x in A, the net of complex numbers {fk(x)}k converges to f(x).
If A is a separable C*-algebra, the weak-* topology is metrizable on bounded subsets. Thus the spectrum of a separable commutative C*-algebra A can be regarded as a metric space. So the topology can be characterized via convergence of sequences.
Equivalently, σ(x) is the range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of γ(x), where γ is the Gelfand representation.
Statement of the commutative Gelfand-Naimark theorem
Let A be a commutative C*-algebra and let X be the spectrum of A. Let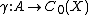be the Gelfand representation defined above.
Theorem. The Gelfand map γ is an isometric *-isomorphism from A onto C0(X).
See the Arveson reference below.
The spectrum of a commutative C*-algebra can also be viewed as the set of all maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
s m of A, with the hull-kernel topology. (See the earlier remarks for the general, commutative Banach algebra case.) For any such m the quotient algebra A/m is one-dimensional (by the Gelfand-Mazur theorem), and therefore any a in A gives rise to a complex-valued function on Y.
In the case of C*-algebras with unit, the spectrum map gives rise to a contravariant functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from the category of C*-algebras with unit and unit-preserving continuous *-homomorphisms, to the category of compact Hausdorff spaces and continuous maps. This functor is one half of a contravariant equivalence
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
between these two categories (its adjoint being the functor that assigns to each compact Hausdorff space X the C*-algebra
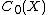). In particular, given compact Hausdorff spaces X and Y, then C(X) is isomorphic to C(Y) (as a C*-algebra) if and only if X is homeomorphic to Y.The 'full' Gelfand–Naimark theorem
Gelfand–Naimark theorem
In mathematics, the Gelfand–Naimark theorem states that an arbitrary C*-algebra A is isometrically *-isomorphic to a C*-algebra of bounded operators on a Hilbert space...
is a result for arbitrary (abstract) noncommutative C*-algebras A, which though not quite analogous to the Gelfand representation, does provide a concrete representation of A as an algebra of operators.
Applications
One of the most significant applications is the existence of a continuous functional calculus for normal elements in C*-algebra A: An element x is normal if and only if x commutes with its adjoint x*, or equivalently if and only if it generates a commutative C*-algebra C*(x). By the Gelfand isomorphism applied to C*(x) this is *-isomorphic to an algebra of continuous functions on a locally compact space. This observation leads almost immediately to:Theorem. Let A be a C*-algebra with identity and x an element of A. Then there is a *-morphism f → f(x) from the algebra of continuous functions on the spectrum σ(x) into A such that
- It maps 1 to the multiplicative identity of A;
- It maps the identity function on the spectrum to x.
This allows us to apply continuous functions to bounded normal operators on Hilbert space.