Spectral theory
Encyclopedia
In mathematics
, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra
and the solutions of systems of linear equations and their generalizations. The theory is connected to that of analytic functions because the spectral properties of an operator are related to analytic functions of the spectral parameter.
in his original formulation of Hilbert space
theory, which was cast in terms of quadratic form
s in infinitely many variables. The original spectral theorem
was therefore conceived as a version of the theorem on principal axes of an ellipsoid, in an infinite-dimensional setting. The later discovery in quantum mechanics
that spectral theory could explain features of atomic spectra
was therefore fortuitous.
There have been three main ways to formulate spectral theory, all of which retain their usefulness. After Hilbert's initial formulation, the later development of abstract Hilbert space
and the spectral theory of a single normal operator
on it did very much go in parallel with the requirements of physics
; particularly at the hands of von Neumann. The further theory built on this to include Banach algebra
s, which can be given abstractly. This development leads to the Gelfand representation
, which covers the commutative case, and further into non-commutative harmonic analysis.
The difference can be seen in making the connection with Fourier analysis. The Fourier transform
on the real line
is in one sense the spectral theory of differentiation
qua differential operator
. But for that to cover the phenomena one has already to deal with generalized eigenfunctions (for example, by means of a rigged Hilbert space
). On the other hand it is simple to construct a group algebra
, the spectrum of which captures the Fourier transform's basic properties, and this is carried out by means of Pontryagin duality
.
One can also study the spectral properties of operators on Banach spaces. For example, compact operator
s on Banach spaces have many spectral properties similar to that of matrices
.
The mathematical theory is not dependent on such physical ideas on a technical level, but there are examples of mutual influence (see for example Mark Kac
's question Can you hear the shape of a drum?). Hilbert's adoption of the term "spectrum" has been attributed to an 1897 paper of Wilhelm Wirtinger
on Hill differential equation (by Jean Dieudonné
), and it was taken up by his students during the first decade of the twentieth century, among them Erhard Schmidt
and Hermann Weyl
. The conceptual basis for Hilbert space
was developed from Hilbert's ideas by Erhard Schmidt and Frigyes Riesz
. It was almost twenty years later, when quantum mechanics
was formulated in terms of the Schrödinger equation
, that the connection was made to atomic spectra; a connection with the mathematical physics of vibration had been suspected before, as remarked by Henri Poincaré
, but rejected for simple quantitative reasons, absent an explanation of the Balmer series
. The later discovery in quantum mechanics that spectral theory could explain features of atomic spectra was therefore fortuitous, rather than being an object of Hilbert's spectral theory.
. We form the transformation:
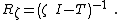
Here I is the identity operator and ζ is a complex number
. The inverse of an operator T, that is T−1, is defined by:
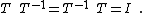
If the inverse exists, T is called regular. If it does not exist, T is called singular.
With these definitions, the resolvent set of T is the set of all complex numbers ζ such that Rζ exists and is bounded. This set often is denoted as ρ(T). The spectrum of T is the set of all complex numbers ζ such that Rζ fails to exist or is unbounded. Often the spectrum of T is denoted by σ(T). The function Rζ for all ζ in ρ(T) (that is, wherever Rζ exists) is called the resolvent
of T. The spectrum of T is therefore the complement of the resolvent set of T in the complex plane. Every eigenvalue of T belongs to σ(T), but σ(T) may contain non-eigenvalues.
This definition applies to a Banach space, but of course other types of space exist as well, for example, topological vector spaces include Banach spaces, but can be more general. On the other hand, Banach spaces include Hilbert space
s, and it is these spaces that find the greatest application and the richest theoretical results. With suitable restrictions, much can be said about the structure of the spectra of transformations in a Hilbert space. In particular, for self-adjoint operator
s, the spectrum lies on the real line
and (in general) is a spectral combination
of a point spectrum of discrete eigenvalues and a continuous spectrum
.
and linear algebra
the spectral theorem establishes conditions under which an operator can be expressed in simple form as a sum of simpler operators. As a full rigorous presentation is not appropriate for this article, we take an approach that avoids much of the rigor and satisfaction of a formal treatment with the aim of being more comprehensible to a non-specialist.
This topic is easiest to describe by introducing the bra-ket notation
of Dirac for operators. As an example, a very particular linear operator L might be written as a dyadic product:
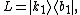
in terms of the "bra"
and the "ket" 
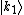. A function 
is described by a ket as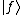 
. The function 
defined on the coordinates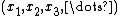 
is denoted as:
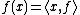
and the magnitude of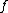
by:
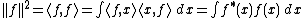
where the notation '*' denotes a complex conjugate. This inner product choice defines a very specific inner product space
, restricting the generality of the arguments that follow.
The effect of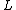
upon a function 
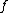is then described as:
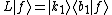
expressing the result that the effect of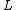
on 
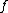is to produce a new function 
multiplied by the inner product represented by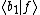 
.
A more general linear operator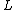
might be expressed as:
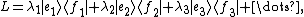
where the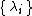
are scalars and the 
are a basis
and the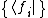
a reciprocal basis for the space. The relation between the basis and the reciprocal basis is described, in part, by:
If such a formalism applies, the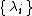
are eigenvalues of 
and the functions 
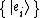are eigenfunctions of 
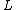. The eigenvalues are in the spectrum of 
.
Some natural questions are: under what circumstances does this formalism work, and for what operators
are expansions in series of other operators like this possible? Can any function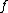 
be expressed in terms of the eigenfunctions (are they a complete set
) and under what circumstances does a point spectrum or a continuous spectrum arise? How do the formalisms for infinite dimensional spaces and finite dimensional spaces differ, or do they differ? Can these ideas be extended to a broader class of spaces? Answering such questions is the realm of spectral theory and requires considerable background in functional analysis
and matrix algebra
.
Using the bra-ket notation of the above section, the identity operator may be written as:
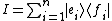
where it is supposed as above that {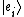
} are a basis
and the {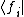
} a reciprocal basis for the space satisfying the relation:
This expression of the identity operation is called a representation or a resolution of the identity., This formal representation satisfies the basic property of the identity:
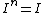
valid for every positive integer n.
Applying the resolution of the identity to any function in the space
, one obtains:
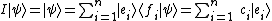
which is the generalized Fourier expansion
of ψ in terms of the basis functions { ei }.
Given some operator equation of the form:
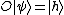
with h in the space, this equation can be solved in the above basis through the formal manipulations:
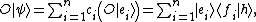
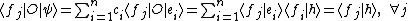
which converts the operator equation to a matrix equation determining the unknown coefficients cj in terms of the generalized Fourier coefficients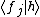
of h and the matrix elements 
=
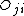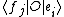of the operator O.
The role of spectral theory arises in establishing the nature and existence of the basis and the reciprocal basis. In particular, the basis might consist of the eigenfunctions of some linear operator L:
with the { λi } the eigenvalues of L from the spectrum of L. Then the resolution of the identity above provides the dyad expansion of L:
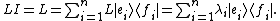
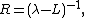
can be evaluated in terms of the eigenfunctions and eigenvalues of L, and the Green's function corresponding to L can be found.
Applying R to some arbitrary function in the space, say φ,
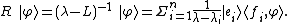
This function has poles in the complex λ-plane at each eigenvalue of L. Thus, using the calculus of residues:
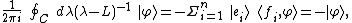
where the line integral is over a contour C that includes all the eigenvalues of L.
Suppose our functions are defined over some coordinates { xj }, that is:
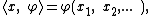
where the bra-kets corresponding to { xj } satisfy:
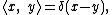
and where δ (x − y) = δ (x1 − y1, x2 − y2, x3 − y3, ...) is the Dirac delta function
.
Then:
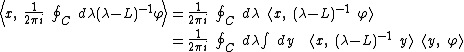
The function G(x, y; λ) defined by:
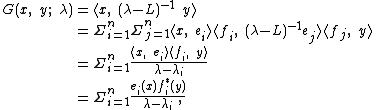
is called the Green's function
for operator L, and satisfies:
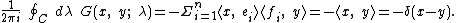
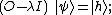
in terms of coordinates:
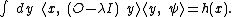
A particular case is λ = 0.
The Green's function of the previous section is:
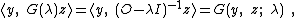
and satisfies:
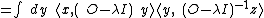
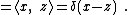
Using this Green's function property:
Then, multiplying both sides of this equation by h(z) and integrating:
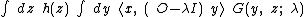
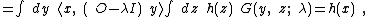
which suggests the solution is:
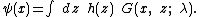
That is, the function ψ(x) satisfying the operator equation is found if we can find the spectrum of O, and construct G, for example by using:
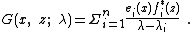
There are many other ways to find G, of course. See the articles on Green's functions and on Fredholm integral equations. It must be kept in mind that the above mathematics is purely formal, and a rigorous treatment involves some pretty sophisticated mathematics, including a good background knowledge of functional analysis
, Hilbert spaces, distributions
and so forth. Consult these articles and the references for more detail.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and the solutions of systems of linear equations and their generalizations. The theory is connected to that of analytic functions because the spectral properties of an operator are related to analytic functions of the spectral parameter.
Mathematical background
The name spectral theory was introduced by David HilbertDavid Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
in his original formulation of Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
theory, which was cast in terms of quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s in infinitely many variables. The original spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
was therefore conceived as a version of the theorem on principal axes of an ellipsoid, in an infinite-dimensional setting. The later discovery in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
that spectral theory could explain features of atomic spectra
Emission spectrum
The emission spectrum of a chemical element or chemical compound is the spectrum of frequencies of electromagnetic radiation emitted by the element's atoms or the compound's molecules when they are returned to a lower energy state....
was therefore fortuitous.
There have been three main ways to formulate spectral theory, all of which retain their usefulness. After Hilbert's initial formulation, the later development of abstract Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and the spectral theory of a single normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
on it did very much go in parallel with the requirements of physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
; particularly at the hands of von Neumann. The further theory built on this to include Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
s, which can be given abstractly. This development leads to the Gelfand representation
Gelfand representation
In mathematics, the Gelfand representation in functional analysis has two related meanings:* a way of representing commutative Banach algebras as algebras of continuous functions;...
, which covers the commutative case, and further into non-commutative harmonic analysis.
The difference can be seen in making the connection with Fourier analysis. The Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
is in one sense the spectral theory of differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
qua differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
. But for that to cover the phenomena one has already to deal with generalized eigenfunctions (for example, by means of a rigged Hilbert space
Rigged Hilbert space
In mathematics, a rigged Hilbert space is a construction designed to link the distribution and square-integrable aspects of functional analysis. Such spaces were introduced to study spectral theory in the broad sense...
). On the other hand it is simple to construct a group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
, the spectrum of which captures the Fourier transform's basic properties, and this is carried out by means of Pontryagin duality
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
.
One can also study the spectral properties of operators on Banach spaces. For example, compact operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
s on Banach spaces have many spectral properties similar to that of matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
.
Physical background
The background in the physics of vibrations has been explained in this way:The mathematical theory is not dependent on such physical ideas on a technical level, but there are examples of mutual influence (see for example Mark Kac
Mark Kac
Mark Kac was a Polish mathematician. His main interest was probability theory. His question, "Can one hear the shape of a drum?" set off research into spectral theory, with the idea of understanding the extent to which the spectrum allows one to read back the geometry. Kac completed his Ph.D...
's question Can you hear the shape of a drum?). Hilbert's adoption of the term "spectrum" has been attributed to an 1897 paper of Wilhelm Wirtinger
Wilhelm Wirtinger
Wilhelm Wirtinger was an Austrian mathematician, working in complex analysis, geometry, algebra, number theory, Lie groups and knot theory.-Biography:...
on Hill differential equation (by Jean Dieudonné
Jean Dieudonné
Jean Alexandre Eugène Dieudonné was a French mathematician, notable for research in abstract algebra and functional analysis, for close involvement with the Nicolas Bourbaki pseudonymous group and the Éléments de géométrie algébrique project of Alexander Grothendieck, and as a historian of...
), and it was taken up by his students during the first decade of the twentieth century, among them Erhard Schmidt
Erhard Schmidt
Erhard Schmidt was a German mathematician whose work significantly influenced the direction of mathematics in the twentieth century. He was born in Tartu, Governorate of Livonia . His advisor was David Hilbert and he was awarded his doctorate from Georg-August University of Göttingen in 1905...
and Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
. The conceptual basis for Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
was developed from Hilbert's ideas by Erhard Schmidt and Frigyes Riesz
Frigyes Riesz
Frigyes Riesz was a mathematician who was born in Győr, Hungary and died in Budapest, Hungary. He was rector and professor at University of Szeged...
. It was almost twenty years later, when quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
was formulated in terms of the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
, that the connection was made to atomic spectra; a connection with the mathematical physics of vibration had been suspected before, as remarked by Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
, but rejected for simple quantitative reasons, absent an explanation of the Balmer series
Balmer series
The Balmer series or Balmer lines in atomic physics, is the designation of one of a set of six different named series describing the spectral line emissions of the hydrogen atom....
. The later discovery in quantum mechanics that spectral theory could explain features of atomic spectra was therefore fortuitous, rather than being an object of Hilbert's spectral theory.
A definition of spectrum
Consider a bounded linear transformation T defined everywhere over a general Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. We form the transformation:
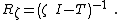
Here I is the identity operator and ζ is a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
. The inverse of an operator T, that is T−1, is defined by:
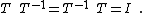
If the inverse exists, T is called regular. If it does not exist, T is called singular.
With these definitions, the resolvent set of T is the set of all complex numbers ζ such that Rζ exists and is bounded. This set often is denoted as ρ(T). The spectrum of T is the set of all complex numbers ζ such that Rζ fails to exist or is unbounded. Often the spectrum of T is denoted by σ(T). The function Rζ for all ζ in ρ(T) (that is, wherever Rζ exists) is called the resolvent
Resolvent formalism
In mathematics, the resolvent formalism is a technique for applying concepts from complex analysis to the study of the spectrum of operators on Hilbert spaces and more general spaces....
of T. The spectrum of T is therefore the complement of the resolvent set of T in the complex plane. Every eigenvalue of T belongs to σ(T), but σ(T) may contain non-eigenvalues.
This definition applies to a Banach space, but of course other types of space exist as well, for example, topological vector spaces include Banach spaces, but can be more general. On the other hand, Banach spaces include Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s, and it is these spaces that find the greatest application and the richest theoretical results. With suitable restrictions, much can be said about the structure of the spectra of transformations in a Hilbert space. In particular, for self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s, the spectrum lies on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
and (in general) is a spectral combination
Decomposition of spectrum (functional analysis)
In mathematics, especially functional analysis, the spectrum of an operator generalizes the notion of eigenvalues. Given an operator, it is sometimes useful to break up the spectrum into various parts...
of a point spectrum of discrete eigenvalues and a continuous spectrum
Continuous spectrum
The spectrum of a linear operator is commonly divided into three parts: point spectrum, continuous spectrum, and residual spectrum.If H is a topological vector space and A:H \to H is a linear map, the spectrum of A is the set of complex numbers \lambda such that A - \lambda I : H \to H is not...
.
What is spectral theory, roughly speaking?
In functional analysisFunctional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
the spectral theorem establishes conditions under which an operator can be expressed in simple form as a sum of simpler operators. As a full rigorous presentation is not appropriate for this article, we take an approach that avoids much of the rigor and satisfaction of a formal treatment with the aim of being more comprehensible to a non-specialist.
This topic is easiest to describe by introducing the bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
of Dirac for operators. As an example, a very particular linear operator L might be written as a dyadic product:
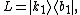
in terms of the "bra"
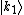and the "ket" . A function is described by a ket as 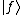. The function defined on the coordinates 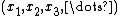is denoted as: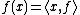and the magnitude of
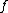by: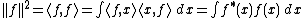where the notation '*' denotes a complex conjugate. This inner product choice defines a very specific inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
, restricting the generality of the arguments that follow.
The effect of
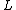upon a function 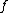is then described as: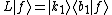expressing the result that the effect of
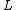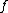on is to produce a new function multiplied by the inner product represented by 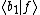.A more general linear operator
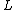might be expressed as: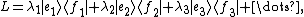where the
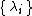are scalars and the are a basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
and the
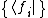a reciprocal basis for the space. The relation between the basis and the reciprocal basis is described, in part, by:If such a formalism applies, the
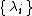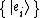are eigenvalues of and the functions are eigenfunctions of 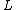. The eigenvalues are in the spectrum of .Some natural questions are: under what circumstances does this formalism work, and for what operators
are expansions in series of other operators like this possible? Can any function 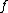be expressed in terms of the eigenfunctions (are they a complete setBasis
Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...
) and under what circumstances does a point spectrum or a continuous spectrum arise? How do the formalisms for infinite dimensional spaces and finite dimensional spaces differ, or do they differ? Can these ideas be extended to a broader class of spaces? Answering such questions is the realm of spectral theory and requires considerable background in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and matrix algebra
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
.
Resolution of the identity
This section continues in the rough and ready manner of the above section using the bra-ket notation, and glossing over the many important and fascinating details of a rigorous treatment. A rigorous mathematical treatment may be found in various references.Using the bra-ket notation of the above section, the identity operator may be written as:
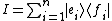
where it is supposed as above that {
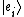} are a basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
and the {
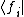} a reciprocal basis for the space satisfying the relation:This expression of the identity operation is called a representation or a resolution of the identity., This formal representation satisfies the basic property of the identity:
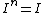
valid for every positive integer n.
Applying the resolution of the identity to any function in the space
, one obtains: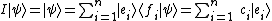which is the generalized Fourier expansion
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
of ψ in terms of the basis functions { ei }.
Given some operator equation of the form:
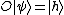
with h in the space, this equation can be solved in the above basis through the formal manipulations:
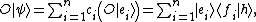
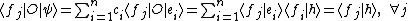
which converts the operator equation to a matrix equation determining the unknown coefficients cj in terms of the generalized Fourier coefficients
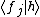of h and the matrix elements 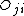= 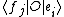of the operator O.The role of spectral theory arises in establishing the nature and existence of the basis and the reciprocal basis. In particular, the basis might consist of the eigenfunctions of some linear operator L:
with the { λi } the eigenvalues of L from the spectrum of L. Then the resolution of the identity above provides the dyad expansion of L:
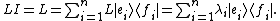
Resolvent operator
Using spectral theory, the resolvent operator R: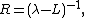can be evaluated in terms of the eigenfunctions and eigenvalues of L, and the Green's function corresponding to L can be found.
Applying R to some arbitrary function in the space, say φ,
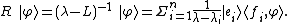
This function has poles in the complex λ-plane at each eigenvalue of L. Thus, using the calculus of residues:
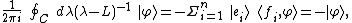
where the line integral is over a contour C that includes all the eigenvalues of L.
Suppose our functions are defined over some coordinates { xj }, that is:
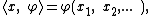
where the bra-kets corresponding to { xj } satisfy:
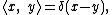
and where δ (x − y) = δ (x1 − y1, x2 − y2, x3 − y3, ...) is the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
.
Then:
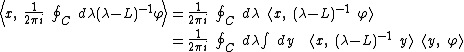
The function G(x, y; λ) defined by:
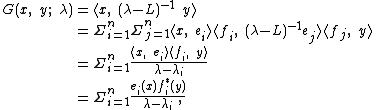
is called the Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
for operator L, and satisfies:
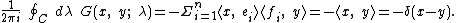
Operator equations
Consider the operator equation: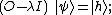in terms of coordinates:
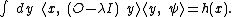
A particular case is λ = 0.
The Green's function of the previous section is:
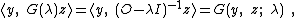
and satisfies:
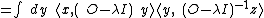
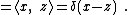
Using this Green's function property:
Then, multiplying both sides of this equation by h(z) and integrating:
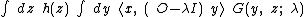
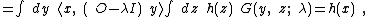
which suggests the solution is:
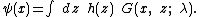
That is, the function ψ(x) satisfying the operator equation is found if we can find the spectrum of O, and construct G, for example by using:
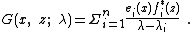
There are many other ways to find G, of course. See the articles on Green's functions and on Fredholm integral equations. It must be kept in mind that the above mathematics is purely formal, and a rigorous treatment involves some pretty sophisticated mathematics, including a good background knowledge of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, Hilbert spaces, distributions
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
and so forth. Consult these articles and the references for more detail.
See also
- Spectrum (functional analysis)Spectrum (functional analysis)In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
, Resolvent formalismResolvent formalismIn mathematics, the resolvent formalism is a technique for applying concepts from complex analysis to the study of the spectrum of operators on Hilbert spaces and more general spaces....
, Decomposition of spectrum (functional analysis)Decomposition of spectrum (functional analysis)In mathematics, especially functional analysis, the spectrum of an operator generalizes the notion of eigenvalues. Given an operator, it is sometimes useful to break up the spectrum into various parts... - Spectral radiusSpectral radiusIn mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
, Spectrum of an operator, Spectral theoremSpectral theoremIn mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized... - Self-adjoint operatorSelf-adjoint operatorIn mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
, Functions of operatorsFunctional calculusIn mathematics, a functional calculus is a theory allowing one to apply mathematical functions to mathematical operators. It is now a branch of the field of functional analysis, connected with spectral theory. In mathematics, a functional calculus is a theory allowing one to apply mathematical...
, Operator theoryOperator theoryIn mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators.... - Sturm–Liouville theory, Integral equationIntegral equationIn mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
s, Fredholm theoryFredholm theoryIn mathematics, Fredholm theory is a theory of integral equations. In the narrowest sense, Fredholm theory concerns itself with the solution of the Fredholm integral equation. In a broader sense, the abstract structure of Fredholm's theory is given in terms of the spectral theory of Fredholm... - Compact operatorCompact operatorIn functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
s, IsospectralIsospectralIn mathematics, two linear operators are called isospectral or cospectral if they have the same spectrum. Roughly speaking, they are supposed to have the same sets of eigenvalues, when those are counted with multiplicity....
operators, CompletenessCompletenessIn general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems... - Lax pairLax pairIn mathematics, in the theory of integrable systems, a Lax pair is a pair of time-dependent matrices or operators that describe the corresponding differential equations. They were introduced by Peter Lax to discuss solitons in continuous media...
s. - Spectral geometrySpectral geometrySpectral geometry is a field in mathematics which concerns relationships between geometric structures of manifolds and spectra of canonically defined differential operators. The case of the Laplace–Beltrami operator on a closed Riemannian manifold has been most intensively studied, although other...
- Spectral graph theorySpectral graph theoryIn mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
- List of functional analysis topics
External links
- Evans M. Harrell II: A Short History of Operator Theory