
Spectrum (functional analysis)
Encyclopedia
In functional analysis
, the concept of the spectrum of a bounded operator
is a generalisation of the concept of eigenvalues for matrices
. Specifically, a complex number
λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible
, where I is the identity operator. The study of spectra and related properties is known as spectral theory
, which has numerous applications, most notably the mathematical formulation
of quantum mechanics
.
The spectrum of an operator on a finite-dimensional
vector space
is precisely the set of eigenvalues. However an operator on an infinite-dimensional space may have additional elements in its spectrum, and may have no eigenvalues. For example, consider the right shift operator R on the Hilbert space
ℓ2
,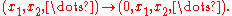
This has no eigenvalues, since if Rx=λx then by expanding this expression we see that x1=0, x2=0, etc. On the other hand 0 is in the spectrum because the operator R − 0 (i.e. R itself) is not invertible: it is not surjective since any vector with non-zero first component is not in its range. In fact every bounded linear operator on a complex
Banach space
must have a non-empty spectrum.
The notion of spectrum extends to densely-defined
unbounded operator
s. In this case a complex number
λ is said to be in the spectrum of such an operator T:D→X (where D is dense in X) if there is no bounded inverse (λI − T)-1:X→D. If T is a closed operator
(which includes the case that T is a bounded operator), boundedness of such inverses follow automatically if the inverse exists at all.
The space of bounded linear operators B(X) on a Banach space X is an example of a unital Banach algebra
. Since the definition of the spectrum does not mention any properties of B(X) except those that any such algebra has, the notion of a spectrum may be generalised to this context by using the same definition verbatim.
is bounded. Therefore the spectrum consists precisely of those λ where λI − T is not bijective.
The spectrum of a given operator T is denoted σ(T), and the resolvent set (the set of points not in the spectrum) is denoted ρ(T).
, bounded
and non-empty
subset of the complex plane
.
If the spectrum were empty, then the resolvent function
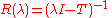
would be defined everywhere on the complex plane and bounded. But it can be shown that the resolvent function R is holomorphic on its domain. By the vector-valued version of Liouville's theorem
, this function is constant, thus everywhere zero as it is zero at infinity. This would be a contradiction.
The boundedness of the spectrum follows from the Neumann series expansion in λ; the spectrum σ(T) is bounded by ||T||. A similar result shows the closedness of the spectrum.
The bound ||T|| on the spectrum can be refined somewhat. The spectral radius
, r(T), of T is the radius of the smallest circle in the complex plane which is centered at the origin and contains the spectrum σ(T) inside of it, i.e.
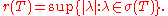
The spectral radius formula says that for any element of a Banach algebra
of a Banach algebra
,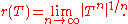
Note that the approximate point spectrum and residual spectrum are not necessarily disjoint (however, the point spectrum and the residual spectrum are).
The following subsections provide more details on the three parts of σ(T) sketched above.
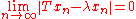 .
.
The set of approximate eigenvalues is known as the approximate point spectrum, denoted by σap(T).
It is easy to see that the eigenvalues lie in the approximate point spectrum.
Example Consider the bilateral shift T on l2(Z) defined by

where the ˆ denotes the zero-th position. Direct calculation shows T has no eigenvalues, but every λ with |λ| = 1 is an approximate eigenvalue; letting xn be the vector
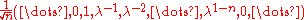
then ||xn|| = 1 for all n, but
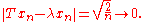
Since T is a unitary operator, its spectrum lie on the unit circle. Therefore the approximate point spectrum of T is its entire spectrum. This is true for a more general class of operators.
A unitary operator is normal
. By spectral theorem
, a bounded operator on a Hilbert space is normal if and only if it is a multiplication operator
. It can be shown that, in general, the approximate point spectrum of a bounded multiplication operator is its spectrum.
, therefore bounded below by 1. But it is not invertible as it is not surjective. The set of λ for which λI - T is injective but does not have dense range is known as the residual spectrum or compression spectrum of T and is denoted by σr(T).
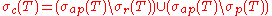 .
.
, then it can be shown that any nonzero λ in the spectrum is an eigenvalue. In other words, the spectrum of such an operator, which was defined as a generalization of the concept of eigenvalues, consists in this case only of the usual eigenvalues, and possibly 0.
If X is a Hilbert space
and T is a normal operator
, then a remarkable result known as the spectral theorem
gives an analogue of the diagonalisation theorem for normal finite-dimensional operators (Hermitian matrices, for example).
s on a Banach space
X, operators which are no longer elements in the Banach algebra B(X). One proceeds in a manner similar to the bounded case. A complex number λ is said to be in the resolvent set, that is, the complement
of the spectrum of a linear operator

if the operator

has a bounded inverse, i.e. if there exists a bounded operator

such that
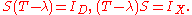
A complex number λ is then in the spectrum if this property fails to hold. One can classify the spectrum in exactly the same way as in the bounded case.
The spectrum of an unbounded operator is in general a closed, possibly empty, subset of the complex plane.
For λ to be in the resolvent (i.e. not in the spectrum), as in the bounded case λI − T must be bijective, since it must have a two-sided inverse. As before if an inverse exists then its linearity is immediate, but in general it may not be bounded, so this condition must be checked separately.
However, boundedness of the inverse does follow directly from its existence if one introduces the additional assumption that T is closed
; this follows from the closed graph theorem
. Therefore, as in the bounded case, a complex number λ lies in the spectrum of a closed operator T if and only if λI − T is not bijective. Note that the class of closed operators includes all bounded operators.
containing a unit
e. Then we define the spectrum σ(x) (or more explicitly σB(x)) of an element x of B to be the set of those complex number
s λ for which λe − x is not invertible in B. This extends the definition for bounded linear operators B(X) on a Banach space X, since B(X) is a Banach algebra.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the concept of the spectrum of a bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
is a generalisation of the concept of eigenvalues for matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. Specifically, a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
, where I is the identity operator. The study of spectra and related properties is known as spectral theory
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
, which has numerous applications, most notably the mathematical formulation
Mathematical formulation of quantum mechanics
The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. Such are distinguished from mathematical formalisms for theories developed prior to the early 1900s by the use of abstract mathematical structures, such as...
of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
The spectrum of an operator on a finite-dimensional
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
is precisely the set of eigenvalues. However an operator on an infinite-dimensional space may have additional elements in its spectrum, and may have no eigenvalues. For example, consider the right shift operator R on the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
ℓ2
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
,
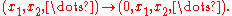
This has no eigenvalues, since if Rx=λx then by expanding this expression we see that x1=0, x2=0, etc. On the other hand 0 is in the spectrum because the operator R − 0 (i.e. R itself) is not invertible: it is not surjective since any vector with non-zero first component is not in its range. In fact every bounded linear operator on a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
must have a non-empty spectrum.
The notion of spectrum extends to densely-defined
Densely-defined operator
In mathematics — specifically, in operator theory — a densely defined operator is a type of partially defined function; in a topological sense, it is a linear operator that is defined "almost everywhere"...
unbounded operator
Unbounded operator
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
s. In this case a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
λ is said to be in the spectrum of such an operator T:D→X (where D is dense in X) if there is no bounded inverse (λI − T)-1:X→D. If T is a closed operator
Closed operator
In mathematics, specifically in functional analysis, closed linear operators are an important class of linear operators on Banach spaces. They are more general than bounded operators, and therefore not necessarily continuous, but they still retain nice enough properties that one can define the...
(which includes the case that T is a bounded operator), boundedness of such inverses follow automatically if the inverse exists at all.
The space of bounded linear operators B(X) on a Banach space X is an example of a unital Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
. Since the definition of the spectrum does not mention any properties of B(X) except those that any such algebra has, the notion of a spectrum may be generalised to this context by using the same definition verbatim.
Spectrum of a bounded operator
The spectrum of a bounded linear operator T acting on a Banach space X is the set of complex numbers λ such that λI − T does not have an inverse that is a bounded linear operator. If λI − T is invertible then that inverse is linear (this follows immediately from the linearity of λI − T), and by the bounded inverse theoremBounded inverse theorem
In mathematics, the bounded inverse theorem is a result in the theory of bounded linear operators on Banach spaces. It states that a bijective bounded linear operator T from one Banach space to another has bounded inverse T−1. It is equivalent to both the open mapping theorem and the closed...
is bounded. Therefore the spectrum consists precisely of those λ where λI − T is not bijective.
The spectrum of a given operator T is denoted σ(T), and the resolvent set (the set of points not in the spectrum) is denoted ρ(T).
Basic properties
The spectrum of a bounded operator T is always a closedClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
, bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
and non-empty
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
subset of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
.
If the spectrum were empty, then the resolvent function
Resolvent formalism
In mathematics, the resolvent formalism is a technique for applying concepts from complex analysis to the study of the spectrum of operators on Hilbert spaces and more general spaces....
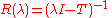
would be defined everywhere on the complex plane and bounded. But it can be shown that the resolvent function R is holomorphic on its domain. By the vector-valued version of Liouville's theorem
Liouville's theorem (complex analysis)
In complex analysis, Liouville's theorem, named after Joseph Liouville, states that every bounded entire function must be constant. That is, every holomorphic function f for which there exists a positive number M such that |f| ≤ M for all z in C is constant.The theorem is considerably improved by...
, this function is constant, thus everywhere zero as it is zero at infinity. This would be a contradiction.
The boundedness of the spectrum follows from the Neumann series expansion in λ; the spectrum σ(T) is bounded by ||T||. A similar result shows the closedness of the spectrum.
The bound ||T|| on the spectrum can be refined somewhat. The spectral radius
Spectral radius
In mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
, r(T), of T is the radius of the smallest circle in the complex plane which is centered at the origin and contains the spectrum σ(T) inside of it, i.e.
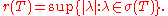
The spectral radius formula says that for any element
 of a Banach algebra
of a Banach algebraBanach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
,
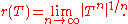
Classification of points in the spectrum of an operator
A bounded operator T on a Banach space is invertible, i.e. has a bounded inverse, if and only if T is bounded below and has dense range. Accordingly, the spectrum of T can be divided into the following parts:- λ ∈ σ(T), if λ - T is not bounded below. In particular, this is the case, if λ - T is not injective, that is, λ is an eigenvalue. The set of eigenvalues is called the point spectrum of T and denoted by σp(T). Alternatively, λ - T could be one-to-one but still not be bounded below. Such λ is not an eigenvalue but still an approximate eigenvalue of T (eigenvalues themselves are also approximate eigenvalues). The set of approximate eigenvalues (which includes the point spectrum) is called the approximate point spectrum of T, denoted by σap(T).
- λ ∈ σ(T), if λ - T does not have dense range. No notation is used to describe the set of all λ, which satisfy this condition, but for a subset: If λ - T does not have dense range but is injective, λ is said to be in the residual spectrum of T, denoted by σr(T) .
Note that the approximate point spectrum and residual spectrum are not necessarily disjoint (however, the point spectrum and the residual spectrum are).
The following subsections provide more details on the three parts of σ(T) sketched above.
Point spectrum
If an operator is not injective (so there is some nonzero x with T(x) = 0), then it is clearly not invertible. So if λ is an eigenvalue of T, one necessarily has λ ∈ σ(T). The set of eigenvalues of T is also called the point spectrum of T, denoted by σp(T) .Approximate point spectrum
More generally, T is not invertible if it is not bounded below; that is, if there is no c > 0 such that ||Tx|| ≥ c||x|| for all . So the spectrum includes the set of approximate eigenvalues, which are those λ such that is not bounded below; equivalently, it is the set of λ for which there is a sequence of unit vectors x1, x2, ... for which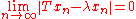 .
.The set of approximate eigenvalues is known as the approximate point spectrum, denoted by σap(T).
It is easy to see that the eigenvalues lie in the approximate point spectrum.
Example Consider the bilateral shift T on l2(Z) defined by

where the ˆ denotes the zero-th position. Direct calculation shows T has no eigenvalues, but every λ with |λ| = 1 is an approximate eigenvalue; letting xn be the vector
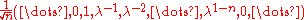
then ||xn|| = 1 for all n, but
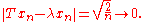
Since T is a unitary operator, its spectrum lie on the unit circle. Therefore the approximate point spectrum of T is its entire spectrum. This is true for a more general class of operators.
A unitary operator is normal
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
. By spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
, a bounded operator on a Hilbert space is normal if and only if it is a multiplication operator
Multiplication operator
In operator theory, a multiplication operator is a linear operator T defined on some vector space of functions and whose value at a function φ is given by multiplication by a fixed function f...
. It can be shown that, in general, the approximate point spectrum of a bounded multiplication operator is its spectrum.
Residual spectrum
An operator may be injective, even bounded below, but not invertible. The unilateral shift on l 2(N) is such an example. This shift operator is an isometryIsometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
, therefore bounded below by 1. But it is not invertible as it is not surjective. The set of λ for which λI - T is injective but does not have dense range is known as the residual spectrum or compression spectrum of T and is denoted by σr(T).
Continuous spectrum
The set of all λ for which λI - T is injective and has dense range, but is not surjective, is called the continuous spectrum of T, denoted by σc(T) . The continuous spectrum therefore consists of those approximate eigenvalues which are not eigenvalues and do not lie in the residual spectrum. That is,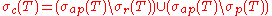 .
.Peripheral spectrum
The peripheral spectrum of an operator is defined as the set of points in its spectrum which have modulus equal to its spectral radius.Further results
If T is a compact operatorCompact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
, then it can be shown that any nonzero λ in the spectrum is an eigenvalue. In other words, the spectrum of such an operator, which was defined as a generalization of the concept of eigenvalues, consists in this case only of the usual eigenvalues, and possibly 0.
If X is a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and T is a normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
, then a remarkable result known as the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
gives an analogue of the diagonalisation theorem for normal finite-dimensional operators (Hermitian matrices, for example).
Spectrum of an unbounded operator
One can extend the definition of spectrum for unbounded operatorUnbounded operator
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
s on a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
X, operators which are no longer elements in the Banach algebra B(X). One proceeds in a manner similar to the bounded case. A complex number λ is said to be in the resolvent set, that is, the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of the spectrum of a linear operator

if the operator

has a bounded inverse, i.e. if there exists a bounded operator

such that
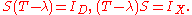
A complex number λ is then in the spectrum if this property fails to hold. One can classify the spectrum in exactly the same way as in the bounded case.
The spectrum of an unbounded operator is in general a closed, possibly empty, subset of the complex plane.
For λ to be in the resolvent (i.e. not in the spectrum), as in the bounded case λI − T must be bijective, since it must have a two-sided inverse. As before if an inverse exists then its linearity is immediate, but in general it may not be bounded, so this condition must be checked separately.
However, boundedness of the inverse does follow directly from its existence if one introduces the additional assumption that T is closed
Closed operator
In mathematics, specifically in functional analysis, closed linear operators are an important class of linear operators on Banach spaces. They are more general than bounded operators, and therefore not necessarily continuous, but they still retain nice enough properties that one can define the...
; this follows from the closed graph theorem
Closed graph theorem
In mathematics, the closed graph theorem is a basic result in functional analysis which characterizes continuous linear operators between Banach spaces in terms of the operator graph.- The closed graph theorem :...
. Therefore, as in the bounded case, a complex number λ lies in the spectrum of a closed operator T if and only if λI − T is not bijective. Note that the class of closed operators includes all bounded operators.
Spectrum of a unital Banach algebra
Let B be a complex Banach algebraBanach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
containing a unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
e. Then we define the spectrum σ(x) (or more explicitly σB(x)) of an element x of B to be the set of those complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s λ for which λe − x is not invertible in B. This extends the definition for bounded linear operators B(X) on a Banach space X, since B(X) is a Banach algebra.

