Bounded inverse theorem
Encyclopedia
In mathematics
, the bounded inverse theorem is a result in the theory of bounded linear operators on Banach space
s. It states that a bijective
bounded linear operator T from one Banach space to another has bounded inverse
T−1. It is equivalent
to both the open mapping theorem
and the closed graph theorem
.
It is necessary that the spaces in question be Banach spaces. For example, consider the space X of sequence
s x : N → R with only finitely many non-zero terms equipped with the supremum norm. The map T : X → X defined by
is bounded, linear and invertible, but T−1 is unbounded. This does not contradict the bounded inverse theorem since X is not complete, and thus is not a Banach space. To see that it's not complete, consider the sequence of sequences x(n) ∈ X given by
converges as n → ∞ to the sequence x(∞) given by
which has all its terms non-zero, and so does not lie in X.
The completion of X is the space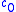
of all sequences that converge to zero, which is a (closed) subspace of the ℓp space
ℓ∞(N), which is the space of all bounded sequences. However, in this case, the map T is not onto, and thus not a bijection. To see this, one need simply note that the sequence
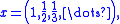
is an element of
, but is not in the range of 
.
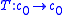Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the bounded inverse theorem is a result in the theory of bounded linear operators on Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. It states that a bijective
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
bounded linear operator T from one Banach space to another has bounded inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
T−1. It is equivalent
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
to both the open mapping theorem
Open mapping theorem
Open mapping theorem may refer to:* Open mapping theorem or Banach–Schauder theorem states that a surjective continuous linear transformation of a Banach space X onto a Banach space Y is an open mapping...
and the closed graph theorem
Closed graph theorem
In mathematics, the closed graph theorem is a basic result in functional analysis which characterizes continuous linear operators between Banach spaces in terms of the operator graph.- The closed graph theorem :...
.
It is necessary that the spaces in question be Banach spaces. For example, consider the space X of sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s x : N → R with only finitely many non-zero terms equipped with the supremum norm. The map T : X → X defined by
is bounded, linear and invertible, but T−1 is unbounded. This does not contradict the bounded inverse theorem since X is not complete, and thus is not a Banach space. To see that it's not complete, consider the sequence of sequences x(n) ∈ X given by
converges as n → ∞ to the sequence x(∞) given by
which has all its terms non-zero, and so does not lie in X.
The completion of X is the space
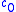of all sequences that converge to zero, which is a (closed) subspace of the ℓp spaceLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
ℓ∞(N), which is the space of all bounded sequences. However, in this case, the map T is not onto, and thus not a bijection. To see this, one need simply note that the sequence
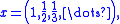
is an element of
, but is not in the range of 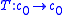.