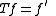Unbounded operator - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, more specifically functional analysis

Functional analysis

Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...

and operator theory

Operator theory

In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....

, the notion of unbounded operator provides an abstract framework for dealing with differential operator

Differential operator

In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...

s, unbounded observable

Observable

In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...

s in quantum mechanics, and other cases.

The term "unbounded operator" can be misleading, since

"unbounded" should be understood as "not necessarily bounded";
"operator" should be understood as "linear operator" (as in the case of "bounded operator");
the domain of the operator is a linear subspace, not necessarily the whole space (in contrast to "bounded operator");
this linear subspace is not necessarily closed; often (but not always) it is assumed to be dense;
in the special case of a bounded operator, still, the domain is usually assumed to be the whole space.

In contrast to bounded operator

Bounded operator

In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...

s, unbounded operators on a given space do not form an algebra, nor even a linear space, because each one is defined on its own domain.

The term "operator" often means "bounded linear operator", but in the context of this article it means "unbounded operator", with the reservations made above. The given space is assumed to be a Hilbert space

Hilbert space

The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

. Some generalizations to Banach space

Banach space

In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...

s and more general topological vector space

Topological vector space

In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...

s are possible.

Short history

The theory of unbounded operators was stimulated by attempts in the late 1920s to put quantum mechanics on a rigorous mathematical foundation. The systematic development of the theory is due to von Neumann and M. Stone. The technique of using the graph to analyze unbounded operators was introduced by von Neumann in.

Definitions and basic properties

Let B₁ and B₂ be Banach space

Banach space

s. An unbounded operator (or simply operator) is a linear map T from a linear subspace D(T) of B₁ — the domain of T — to the space B₂. Contrary to the usual convention, T may not be defined on the whole space B₁. Two operators are equal if they have the common domain and they coincide on that common domain.

An operator T is said to be closed
Closed operator
In mathematics, specifically in functional analysis, closed linear operators are an important class of linear operators on Banach spaces. They are more general than bounded operators, and therefore not necessarily continuous, but they still retain nice enough properties that one can define the...

if its graph Γ(T) is a closed set

Closed set

In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...

. (Here, the graph Γ(T) is a linear subspace of the direct sum , defined as the set of all pairs , where x runs over the domain of T). Explicitly, this means that for every sequence (x_n) of points from the domain of T such that x_n converge to some x and Tx_n converge to some y, it holds that x belongs to the domain of T and . The closedness can also be formulated in terms of the graph norm: an operator T is closed if and only if its domain D(T) is a complete space

Complete space

In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....

with respect to the norm:

An operator T is said to be densely defined if its domain is dense

Dense set

In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...

in B₁. This also includes operators defined on the entire space B₁, since the whole space is dense in itself. The denseness of the domain is necessary and sufficient for the existence of the adjoint and the transpose; see the next section.

If is closed, densely defined and continuous on its domain, then it is defined on B₁.

A densely defined operator T on a Hilbert space

Hilbert space

H is called bounded from below if is a positive operator for some real number a. That is, for all x in the domain of T. If both T and (–T) are bounded from below then T is bounded.

Example

The classical differentiation operator

defined on the set D(T) of all continuously differentiable functions f on the closed interval [0,1] is an unbounded operator H → H where H=L₂[0,1] is the Hilbert space of all square integrable functions on [0,1] (more exactly, equivalence classes; the functions must be measurable, either real-valued or complex-valued). The definition of T is correct, since a continuous (the more so, continuously differentiable) function cannot vanish almost everywhere, unless it vanishes everywhere.

This is a linear operator, since a linear combination af+bg of two continuously differentiable functions f, g is also continuously differentiable, and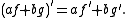

The operator is not bounded. For example, the functions f_n defined on [0,1] by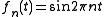

satisfy

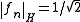but

The operator is densely defined, and not closed.

The same operator can be treated as operator B → B for many Banach spaces B, and is still not bounded. However, it is bounded as operator B₁ → B₂ for some pairs of Banach spaces B₁, B₂, and also as operator B → B for some topological vector spaces B.

Adjoint

The adjoint of an unbounded operator can be defined in two equivalent ways. First, it can be defined in a way analogous to how we define the adjoint of a bounded operator. Namely, the adjoint T^∗ : H₂ → H₁ of T is defined as an operator with the property:

More precisely, T^∗ is defined in the following way. If y is such that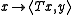

is a continuous linear functional on the domain of T, then, after extending it to the whole space via the Hahn–Banach theorem

Hahn–Banach theorem

In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...

, we can find a z such that

since the dual of a Hilbert space can be identified with the set of linear functionals given by the inner product. For each y, z is uniquely determined if and only if the linear functional is densely defined; i.e., T is densely defined. Finally, we let T^∗y = z, completing the construction of T^∗. Note that T^∗ exists if and only if T is densely defined.

By definition, the domain of T^∗ consists of elements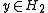

such that

is continuous on the domain of T. Consequently, the domain of T^∗ could be anything; it could be trivial (i.e., contains only zero) It may happen that the domain of T^∗ is a closed hyperplane

Hyperplane

A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...

and T^∗ vanishes everywhere on the domain. Thus, boundedness of T^∗ on its domain does not imply boundedness of T. On the other hand, if T^∗ is defined on the whole space then T is bounded on its domain and therefore can be extended by continuity to a bounded operator on the whole space. If the domain of T^∗ is dense, then it has its adjoint T^∗∗. A closed densely defined operator T is bounded if and only if T^∗ is bounded.

The other equivalent definition of the adjoint can be obtained by noticing a general fact: define a linear operator

. (Since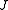

is an isometric surjection, it is unitary.) We then have:

is the graph of some operator S if and only if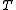

is densely defined. A simple calculation shows that this "some" S satisfies:

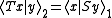for every x in the domain of T. Thus, S is the adjoint of T.

It follows immediately from the above definition that the adjoint T^∗ is closed. In particular, a self-adjoint operator (i.e., T = T^∗) is closed. An operator T is closed and densely defined if and only if T^∗∗ = T.

Some well-known properties for bounded operators generalize to closed densely defined operators. The kernel of a closed operator is closed. Moreover, the kernel of a closed densely defined operator T : H₁ → H₂ coincides with the orthogonal complement of the range of the adjoint. That is,

von Neumann's theorem

Von Neumann's theorem

In mathematics, von Neumann's theorem is a result in the operator theory of linear operators on Hilbert spaces.-Statement of the theorem:Let G and H be Hilbert spaces, and let T : dom ⊆ G → H be a densely-defined operator from G into H...

states that T^∗T and TT^∗ are self-adjoint, and that I + T^∗T and I + TT^∗ both have bounded inverses. If

has trivial kernel,

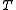has dense range (by the above identity.) Moreover, T is surjective if and only if there is a

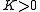such that

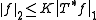for every

.
(This is essentially a variant of the so-called closed range theorem

Closed range theorem

In the mathematical theory of Banach spaces, the closed range theorem gives necessary and sufficient conditions for a closed densely defined operator to have closed range...

.) In particular, T has closed range if and only if T^∗ has closed range.

In contrast to the bounded case, it is not necessary that we have: (TS)^∗ = S^∗T^∗, since, for example, it is even possible that (TS)^∗ doesn't exist. This is, however, the case if, for example, T is bounded.

A densely defined, closed operator T is called normal
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....

if it satisfies the following equivalent conditions:

T^∗T = T T^∗;
the domain of T is equal to the domain of T^∗, and for every x in this domain;
there exist self-adjoint operators A, B such that T = A + iB, T^∗ = A – iB, and for every x in the domain of T.

Every self-adjoint operator is normal.

Transpose

Let T : B₁ → B₂ be an operator between Banach spaces. Then the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...

(or dual)

of T is an operator satisfying: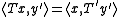

for all x in B₁ and y in B₂^*. Here, we used the notation: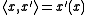

.

The necessary and sufficient condition for the transpose of T to exist is that T is densely defined (for essentially the same reason as to adjoints, as discussed above.)

For any Hilbert space H, there is the anti-linear isomorphism:

given by

where

.
Through this isomorphism, the transpose T^' relates to the adjoint T^∗ in the following way:

,
where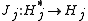

. (For the finite-dimensional case, this corresponds to the fact that the adjoint of a matrix is its conjugate transpose.) Note that this gives the definition of adjoint in terms of a transpose.

Symmetric operators and self-adjoint operators

A densely defined operator T is symmetric if

for all elements x and y in the domain of T.

An operator T is said to be self-adjoint if T^∗ = T. Note that, when T is self-adjoint, the existence of the adjoint implies that T is dense and since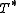

is necessarily closed,

is closed.

A densely defined operator T is symmetric, if the subspace Γ ( T ) is orthogonal to its image J ( Γ ( T ) ) under J.

Equivalently, an operator T is self-adjoint if it is densely defined, closed, symmetric, and satisfies the fourth condition: both operators T – i, T + i are surjective, that is, map the domain of T onto the whole space H. In other words: for every x in H there exist y and z in the domain of T such that Ty – iy = x and Tz + iz = x.

An operator T is self-adjoint, if the two subspaces Γ ( T ), J ( Γ ( T ) ) are orthogonal and their sum is the whole space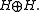

A densely defined operator T is symmetric if T^∗ is an extension of T (see below).

This approach does not cover non-densely defined closed operators. Non-densely defined symmetric operators can be defined directly or via graphs, but not via adjoint operators.

A symmetric operator is often studied via its Cayley transform

Cayley transform

In mathematics, the Cayley transform, named after Arthur Cayley, has a cluster of related meanings. As originally described by , the Cayley transform is a mapping between skew-symmetric matrices and special orthogonal matrices. In complex analysis, the Cayley transform is a conformal mapping in...

.

An operator T is symmetric if and only if its quadratic form is real, that is, the number

is real for all x in the domain of T.

A densely defined closed symmetric operator T is self-adjoint if and only if T^∗ is symmetric. It may happen that it is not.

A densely defined operator T is called positive (or nonnegative) if its quadratic form is nonnegative, that is,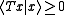

for all x in the domain of T. Such operator is necessarily symmetric.

The operator T^∗T is self-adjoint and positive for every densely defined, closed T.

The spectral theorem applies to self-adjoint operators and moreover, to normal operators, but not to densely defined, closed operators in general, since in this case the spectrum can be empty.

A symmetric operator defined everywhere is closed, therefore bounded, which is the Hellinger–Toeplitz theorem

Hellinger–Toeplitz theorem

In functional analysis, a branch of mathematics, the Hellinger–Toeplitz theorem states that an everywhere defined symmetric operator on a Hilbert space is bounded. By definition, an operator A is symmetric if \langle A x | y \rangle = \langle x | A y\rangle for all x, y in the domain of A...

Extension-related

By definition, an operator T is an extension of an operator S if Γ (S) ⊆ Γ (T). An equivalent direct definition: for every x in the domain of S, x belongs to the domain of T and Sx = Tx.

Note that an everywhere defined extension exists for every operator, which is a purely algebraic fact explained at Discontinuous linear map#General existence theorem and based on the axiom of choice. If the given operator is not bounded then the extension is a discontinuous linear map

Discontinuous linear map

In mathematics, linear maps form an important class of "simple" functions which preserve the algebraic structure of linear spaces and are often used as approximations to more general functions . If the spaces involved are also topological spaces , then it makes sense to ask whether all linear maps...

. It is of little use since it cannot preserve important properties of the given operator (see below), and usually is highly non-unique.

An operator T is called closable if it satisfies the following equivalent conditions:

T has a closed extension;
the closure of the graph of T is the graph of some operator;
for every sequence (x_n) of points from the domain of T such that x_n converge to 0 and also Tx_n converge to some y it holds that y = 0.

Not all operators are closable.

A closable operator T has the least closed extension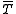

called the closure of T. The closure of the graph of T is equal to the graph of

Other, non-minimal closed extensions may exist.

A densely defined operator T is closable if and only if T^∗ is densely defined. In this case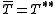

and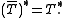

If S is densely defined and T is an extension of S then S^∗ is an extension of T^∗.

Every symmetric operator is closable.

A symmetric operator is called maximal symmetric if it has no symmetric extensions, except for itself.

Every self-adjoint operator is maximal symmetric. The converse is wrong.

An operator is called essentially self-adjoint if its closure is self-adjoint.

An operator is essentially self-adjoint if and only if it has one and only one self-adjoint extension.

An operator may have more than one self-adjoint extension, and even a continuum of them.

A densely defined, symmetric operator T is essentially self-adjoint if and only if both operators T – i, T + i have dense range.

Let T be a densely defined operator. Denoting the relation "T is an extension of S" by S ⊂ T (a conventional abbreviation for Γ(S) ⊆ Γ(T)) one has the following.

If T is symmetric then T ⊂ T^∗∗ ⊂ T^∗.
If T is closed and symmetric then T = T^∗∗ ⊂ T^∗.
If T is self-adjoint then T = T^∗∗ = T^∗.
If T is essentially self-adjoint then T ⊂ T^∗∗ = T^∗.

Importance of self-adjoint operators

The class of self-adjoint operators is especially important in mathematical physics. Every self-adjoint operator is densely defined, closed and symmetric. The converse holds for bounded operators but fails in general. Self-adjointness is substantially more restricting than these three properties. The famous spectral theorem holds for self-adjoint operators. In combination with Stone's theorem on one-parameter unitary groups

Stone's theorem on one-parameter unitary groups

In mathematics, Stone's theorem on one-parameter unitary groups is a basic theorem of functional analysis which establishes a one-to-one correspondence between self-adjoint operators on a Hilbert space H and one-parameter families of unitary operators...

it shows that self-adjoint operators are precisely the infinitesimal generators of strongly continuous one-parameter unitary groups, see Self-adjoint operator#Self adjoint extensions in quantum mechanics. Such unitary groups are especially important for describing time evolution

Time evolution

Time evolution is the change of state brought about by the passage of time, applicable to systems with internal state . In this formulation, time is not required to be a continuous parameter, but may be discrete or even finite. In classical physics, time evolution of a collection of rigid bodies...

in classical and quantum mechanics.