
Closed operator
Encyclopedia
In mathematics
, specifically in functional analysis
, closed linear operators are an important class of linear operators on Banach space
s. They are more general than bounded operator
s, and therefore not necessarily continuous
, but they still retain nice enough properties that one can define the spectrum
and (with certain assumptions) functional calculus
for such operators. Many important linear operators which fail to be bounded turn out to be closed, such as the derivative
and a large class of differential operator
s.
Let be two Banach space
be two Banach space
s. A linear operator
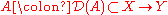
is closed if for every sequence
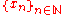 in
in  converging
converging
to such that
such that  as
as  one has
one has 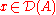 and
and 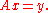 Equivalently,
Equivalently,  is closed if its graph is closed
is closed if its graph is closed
in the direct sum
Given a linear operator , not necessarily closed, if the closure of its graph in
, not necessarily closed, if the closure of its graph in  happens to be the graph of some operator, that operator is called the closure of
happens to be the graph of some operator, that operator is called the closure of  , and we say that
, and we say that  is closable. Denote the closure of
is closable. Denote the closure of  by
by  It follows easily that
It follows easily that  is the restriction
is the restriction
of to
to 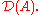
A core of a closable operator is a subset
 of
of 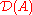 such that the closure of the restriction of
such that the closure of the restriction of  to
to  is
is 
operator
where the Banach space X=Y is the space C[a, b] of all continuous function
s on an interval
[a, b]. If one takes its domain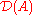 to be
to be  , then A is a closed operator, which is not bounded. (Note that one could also set
, then A is a closed operator, which is not bounded. (Note that one could also set 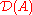 to be the set of all differentiable functions including those with non-continuous derivative. That operator is not closed!)
to be the set of all differentiable functions including those with non-continuous derivative. That operator is not closed!)
If one takes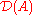 to be instead the set of all infinitely differentiable
to be instead the set of all infinitely differentiable
functions, A will no longer be closed, but it will be closable, with the closure being its extension defined on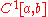 .
.
See also densely defined operator and unbounded operator
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, closed linear operators are an important class of linear operators on Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. They are more general than bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
s, and therefore not necessarily continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, but they still retain nice enough properties that one can define the spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
and (with certain assumptions) functional calculus
Functional calculus
In mathematics, a functional calculus is a theory allowing one to apply mathematical functions to mathematical operators. It is now a branch of the field of functional analysis, connected with spectral theory. In mathematics, a functional calculus is a theory allowing one to apply mathematical...
for such operators. Many important linear operators which fail to be bounded turn out to be closed, such as the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
and a large class of differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s.
Let
 be two Banach space
be two Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. A linear operator
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
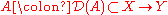
is closed if for every sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
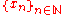 in
in  converging
convergingLimit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
to
 such that
such that  as
as  one has
one has 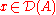 and
and 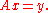 Equivalently,
Equivalently,  is closed if its graph is closed
is closed if its graph is closedClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
in the direct sum

Given a linear operator
 , not necessarily closed, if the closure of its graph in
, not necessarily closed, if the closure of its graph in  happens to be the graph of some operator, that operator is called the closure of
happens to be the graph of some operator, that operator is called the closure of  , and we say that
, and we say that  is closable. Denote the closure of
is closable. Denote the closure of  by
by  It follows easily that
It follows easily that  is the restriction
is the restrictionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of
 to
to 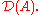
A core of a closable operator is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
 of
of 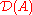 such that the closure of the restriction of
such that the closure of the restriction of  to
to  is
is 
Basic Properties
The following properties are easily checked:- Any closed linear operator defined on the whole space
 is bounded. This is the closed graph theoremClosed graph theoremIn mathematics, the closed graph theorem is a basic result in functional analysis which characterizes continuous linear operators between Banach spaces in terms of the operator graph.- The closed graph theorem :...
is bounded. This is the closed graph theoremClosed graph theoremIn mathematics, the closed graph theorem is a basic result in functional analysis which characterizes continuous linear operators between Banach spaces in terms of the operator graph.- The closed graph theorem :...
; - If
 is closed then
is closed then  is closed where
is closed where 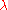 is a scalar and
is a scalar and 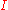 is the identity functionIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
is the identity functionIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
; - If
 is closed, then its kernel (or nullspace) is a closed subspace of
is closed, then its kernel (or nullspace) is a closed subspace of  ;
; - If
 is closed and injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
is closed and injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
, then its inverseInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
 is also closed;
is also closed; - An operator
 admits a closure if and only if for every pair of sequences
admits a closure if and only if for every pair of sequences 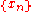 and
and 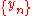 in
in 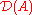 both converging to
both converging to  , such that both
, such that both 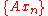 and
and 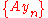 converge, one has
converge, one has 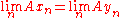 .
.
Example
Consider the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
operator

where the Banach space X=Y is the space C[a, b] of all continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s on an interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[a, b]. If one takes its domain
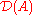 to be
to be  , then A is a closed operator, which is not bounded. (Note that one could also set
, then A is a closed operator, which is not bounded. (Note that one could also set 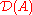 to be the set of all differentiable functions including those with non-continuous derivative. That operator is not closed!)
to be the set of all differentiable functions including those with non-continuous derivative. That operator is not closed!)If one takes
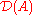 to be instead the set of all infinitely differentiable
to be instead the set of all infinitely differentiableSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
functions, A will no longer be closed, but it will be closable, with the closure being its extension defined on
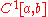 .
.See also densely defined operator and unbounded operator
Unbounded operator
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
.

