Closed range theorem
Encyclopedia
In the mathematical
theory of Banach space
s, the closed range theorem gives necessary and sufficient conditions for a closed densely defined operator to have closed
range. The theorem was proved by Stefan Banach
in his 1932 Théorie des opérations linéaires.
Let X and Y be Banach spaces, T : D(X) → Y a closed linear operator whose domain D(X) is dense in X, and
its transpose. The theorem asserts that the following conditions are equivalent:
Several corollaries are immediate from the theorem. For instance, a densely defined closed operator T as above has R(T) = Y if and only if the transpose has a continuous inverse. Similarly,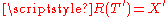
if and only if T has a continuous inverse.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
theory of Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s, the closed range theorem gives necessary and sufficient conditions for a closed densely defined operator to have closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
range. The theorem was proved by Stefan Banach
Stefan Banach
Stefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....
in his 1932 Théorie des opérations linéaires.
Let X and Y be Banach spaces, T : D(X) → Y a closed linear operator whose domain D(X) is dense in X, and
its transpose. The theorem asserts that the following conditions are equivalent:- R(T), the range of T, is closed in Y
-
, the range of 
, is closed in 
, the dual of X -
-
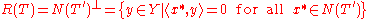
Several corollaries are immediate from the theorem. For instance, a densely defined closed operator T as above has R(T) = Y if and only if the transpose has a continuous inverse. Similarly,
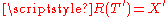if and only if T has a continuous inverse.