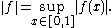Discontinuous linear map
Encyclopedia
In mathematics
, linear maps form an important class of "simple" functions
which preserve the algebraic structure of linear spaces and are often used as approximations to more general functions (see linear approximation
). If the spaces involved are also topological space
s (that is, topological vector space
s), then it makes sense to ask whether all linear maps are continuous. It turns out that for maps defined on infinite-dimensional topological vector spaces (e.g., infinite-dimensional normed spaces), the answer is generally no: there exist discontinuous linear maps. If the domain of definition is complete
, such maps can be proven to exist, but the proof relies on the axiom of choice and does not provide an explicit example.
and so by the triangle inequality
,
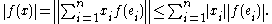
Letting
and using the fact that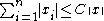
for some C>0 which follows from the fact that any two norms on a finite-dimensional space are equivalent, one finds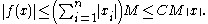
Thus, f is a bounded linear operator and so is continuous.
If X is infinite-dimensional, this proof will fail as there is no guarantee that the supremum
M exists. If Y is the zero space {0}, the only map between X and Y is the zero map which is trivially continuous. In all other cases, when X is infinite dimensional and Y is not the zero space, one can find a discontinuous map from X to Y.
For example, consider the space X of real-valued smooth function
s on the interval [0, 1] with the uniform norm, that is,
The derivative
at a point map, given by
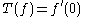
defined on X and with real values, is linear, but not continuous. Indeed, consider the sequence
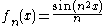
for n≥1. This sequence converges uniformly to the constantly zero function, but
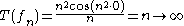
as n→∞ instead of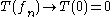
which would hold for a continuous map. Note that T is real-valued, and so is actually a linear functional
on X (an element of the algebraic dual space
X*). The linear map X → X which assigns to each function its derivative is similarly discontinuous. Note that although the derivative operator is not continuous, it is closed
.
The fact that the domain is not complete here is important. Discontinuous operators on complete spaces require a little more work.
s as a vector space over the rationals is known as a Hamel basis (note that some authors use this term in a broader sense to mean an algebraic basis of any vector space). Note that any two noncommensurable
numbers, say 1 and π, are linearly independent. One may find a Hamel basis containing them, and define a map f from R to R so that f(π) = 0, f acts as the identity on the rest of the Hamel basis, and extend to all of R by linearity. Let {rn}n be any sequence of rationals which converges to π. Then limn f(rn) = π, but f(π) = 0. By construction, f is linear over Q (not over R), but not continuous. Note that f is also not measurable
; an additive
real function is linear if and only if it is measurable, so for every such function there is a Vitali set
. The construction of f relies on the axiom of choice.
This example can be extended into a general theorem about the existence of discontinuous linear maps on any infinite-dimensional normed space (as long as the codomain is not trivial).
If X is infinite-dimensional, to show the existence of a linear functional which is not continuous then amounts to constructing f which is not bounded. For that, consider a sequence
(en)n (n ≥ 1) of linearly independent vectors in X. Define
for each n = 1, 2, ... Complete this sequence of linearly independent vectors to a vector space basis of X, and define T at the other vectors in the basis to be zero. T so defined will extend uniquely to a linear map on X, and since it is clearly not bounded, it is not continuous.
Notice that by using the fact that any set of linearly independent vectors can be completed to a basis, we implicitly used the axiom of choice, which was not needed for the concrete example in the previous section.
s). In analysis as it is usually practiced by working mathematicians, the axiom of choice is always employed (it is an axiom of ZFC set theory
); thus, to the analyst, all infinite dimensional topological vector spaces admit discontinuous linear maps.
On the other hand, in 1970 Robert M. Solovay
exhibited a model of set theory
in which every set of reals is measurable. This implies that there are no discontinuous linear real functions. Clearly AC does not hold in the model.
Solovay's result shows that it is not necessary to assume that all infinite-dimensional vector spaces admit discontinuous linear maps, and there are schools of analysis which adopt a more constructivist
viewpoint. For example H. G. Garnir, in searching for so-called "dream spaces" (topological vector spaces on which every linear map into a normed space is continuous), was led to adopt ZF + DC + BP (dependent choice is a weakened form and the Baire property is a negation of strong AC) as his axioms to prove the Garnir-Wright closed graph theorem which states, among other things, that any linear map from an F-space
to a TVS is continuous. Going to the extreme of constructivism, there is Ceitin's theorem, which states that every map is continuous (where this is to be understood in an appropriate framework). Such stances are held by only a small minority of working mathematicians.
The upshot is that it is not possible to obviate the need for AC; it is consistent with set theory without AC that there are no discontinuous linear maps. A corollary is that constructible discontinuous operators such as the derivative cannot be everywhere-defined on a complete space.
, a class of operators which share some of the features of continuous operators. It makes sense to ask the analogous question about whether all linear operators on a given space are closed. The closed graph theorem
asserts that all everywhere-defined closed operators on a complete domain are continuous, so in the context of discontinuous closed operators, one must allow for operators which are not defined everywhere. Among operators which are not everywhere-defined, one can consider densely-defined operators without loss of generality.
Thus let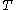
be a map 
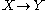with domain 
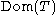. The graph 
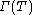of an operator 
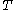which is not everywhere-defined will admit a distinct closure 
. If the closure of the graph is itself the graph of some operator 
, 
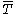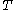is called closable, and 
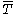is called the closure of 
.
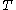So the right question to ask about linear operators that are densely-defined is whether they are closable. The answer is not necessarily; one can prove that every infinite-dimensional normed space admits a nonclosable linear operator. The proof requires the axiom of choice and so is in general nonconstructive, though again, if X is not complete, there are constructible examples.
In fact, an example of a linear operator whose graph has closure all of X×Y can be given. Such an operator is not closable. Let X be the space of polynomial functions from [0,1] to R and Y the space of polynomial functions from [2,3] to R. They are subspaces of C([0,1]) and C([2,3]) respectively, and so normed spaces. Define an operator T which takes the polynomial function x ↦ p(x) to on [0,1] to the same function on [2,3]. As a consequence of the Stone-Weierstrass theorem
, the graph of this operator is dense in X×Y, so this provides a sort of maximally discontinuous linear map (confer nowhere continuous function). Note that X is not complete here, as must be the case when there is such a constructible map.
of a topological vector space is the collection of continuous linear maps from the space into the underlying field. Thus the failure of some linear maps to be continuous for infinite-dimensional normed spaces implies that for these spaces, one needs to distinguish the algebraic dual space from the continuous dual space which is then a proper subset. It illustrates the fact that an extra dose of caution is needed in doing analysis on infinite-dimensional spaces as compared to finite-dimensional ones.
, which applies to all locally convex spaces, guarantees the existence of many continuous linear functionals, and so a large dual space. In fact, to every convex set, the Minkowski gauge associates a continuous linear functional
. The upshot is that spaces with fewer convex sets have fewer functionals, and in the worst case scenario, a space may have no functionals at all other than the zero functional. This is the case for the Lp(R,dx)
spaces with 0<p<1, from which it follows that these spaces are nonconvex. Note that here is indicated the Lebesgue measure
on the real line. There are other Lp spaces with 0<p<1 which do have nontrivial dual spaces.
Another such example is the space of real-valued measurable function
s on the unit interval with quasinorm given by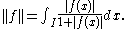
This non-locally convex space has a trivial dual space.
One can consider even more general spaces. For example, the existence of a homomorphism between complete separable metric group
s can also be shown nonconstructively.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, linear maps form an important class of "simple" functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
which preserve the algebraic structure of linear spaces and are often used as approximations to more general functions (see linear approximation
Linear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
). If the spaces involved are also topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s (that is, topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s), then it makes sense to ask whether all linear maps are continuous. It turns out that for maps defined on infinite-dimensional topological vector spaces (e.g., infinite-dimensional normed spaces), the answer is generally no: there exist discontinuous linear maps. If the domain of definition is complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
, such maps can be proven to exist, but the proof relies on the axiom of choice and does not provide an explicit example.
If a linear map is finite dimensional, the linear map is continuous
Let X and Y be two normed spaces and f a linear map from X to Y. If X is finite-dimensional, choose a base (e1, e2, …, en) in X which may be taken to be unit vectors. Then,and so by the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
,
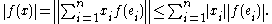
Letting
and using the fact that
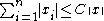
for some C>0 which follows from the fact that any two norms on a finite-dimensional space are equivalent, one finds
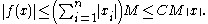
Thus, f is a bounded linear operator and so is continuous.
If X is infinite-dimensional, this proof will fail as there is no guarantee that the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
M exists. If Y is the zero space {0}, the only map between X and Y is the zero map which is trivially continuous. In all other cases, when X is infinite dimensional and Y is not the zero space, one can find a discontinuous map from X to Y.
A concrete example
Examples of discontinuous linear maps are easy to construct in spaces that are not complete; on any Cauchy sequence of independent vectors which does not have a limit, a linear operator may grow without bound. In a sense, the linear operators are not continuous because the space has "holes".For example, consider the space X of real-valued smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s on the interval [0, 1] with the uniform norm, that is,
The derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
at a point map, given by
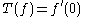
defined on X and with real values, is linear, but not continuous. Indeed, consider the sequence
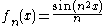
for n≥1. This sequence converges uniformly to the constantly zero function, but
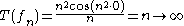
as n→∞ instead of
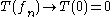which would hold for a continuous map. Note that T is real-valued, and so is actually a linear functionalLinear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
on X (an element of the algebraic dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
X*). The linear map X → X which assigns to each function its derivative is similarly discontinuous. Note that although the derivative operator is not continuous, it is closed
Closed operator
In mathematics, specifically in functional analysis, closed linear operators are an important class of linear operators on Banach spaces. They are more general than bounded operators, and therefore not necessarily continuous, but they still retain nice enough properties that one can define the...
.
The fact that the domain is not complete here is important. Discontinuous operators on complete spaces require a little more work.
A nonconstructive example
An algebraic basis for the real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s as a vector space over the rationals is known as a Hamel basis (note that some authors use this term in a broader sense to mean an algebraic basis of any vector space). Note that any two noncommensurable
Commensurability (mathematics)
In mathematics, two non-zero real numbers a and b are said to be commensurable if a/b is a rational number.-History of the concept:...
numbers, say 1 and π, are linearly independent. One may find a Hamel basis containing them, and define a map f from R to R so that f(π) = 0, f acts as the identity on the rest of the Hamel basis, and extend to all of R by linearity. Let {rn}n be any sequence of rationals which converges to π. Then limn f(rn) = π, but f(π) = 0. By construction, f is linear over Q (not over R), but not continuous. Note that f is also not measurable
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
; an additive
Additive function
In mathematics the term additive function has two different definitions, depending on the specific field of application.In algebra an additive function is a function that preserves the addition operation:for any two elements x and y in the domain. For example, any linear map is additive...
real function is linear if and only if it is measurable, so for every such function there is a Vitali set
Vitali set
In mathematics, a Vitali set is an elementary example of a set of real numbers that is not Lebesgue measurable, found by . The Vitali theorem is the existence theorem that there are such sets. There are uncountably many Vitali sets, and their existence is proven on the assumption of the axiom of...
. The construction of f relies on the axiom of choice.
This example can be extended into a general theorem about the existence of discontinuous linear maps on any infinite-dimensional normed space (as long as the codomain is not trivial).
General existence theorem
Discontinuous linear maps can be proven to exist more generally even if the space is complete. Let X and Y be normed spaces over the field K where K = R or K = C. Assume that X is infinite-dimensional and Y is not the zero space. We will find a discontinuous linear map f from X to K, which will imply the existence of a discontinuous linear map g from X to Y given by the formula g(x) = f(x)y0 where y0 is an arbitrary nonzero vector in Y.If X is infinite-dimensional, to show the existence of a linear functional which is not continuous then amounts to constructing f which is not bounded. For that, consider a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
(en)n (n ≥ 1) of linearly independent vectors in X. Define
for each n = 1, 2, ... Complete this sequence of linearly independent vectors to a vector space basis of X, and define T at the other vectors in the basis to be zero. T so defined will extend uniquely to a linear map on X, and since it is clearly not bounded, it is not continuous.
Notice that by using the fact that any set of linearly independent vectors can be completed to a basis, we implicitly used the axiom of choice, which was not needed for the concrete example in the previous section.
Axiom of choice
As noted above, the axiom of choice (AC) is used in the general existence theorem of discontinuous linear maps. In fact, there are no constructive examples of discontinuous linear maps with complete domain (for example, Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s). In analysis as it is usually practiced by working mathematicians, the axiom of choice is always employed (it is an axiom of ZFC set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
); thus, to the analyst, all infinite dimensional topological vector spaces admit discontinuous linear maps.
On the other hand, in 1970 Robert M. Solovay
Robert M. Solovay
Robert Martin Solovay is an American mathematician specializing in set theory.Solovay earned his Ph.D. from the University of Chicago in 1964 under the direction of Saunders Mac Lane, with a dissertation on A Functorial Form of the Differentiable Riemann–Roch theorem...
exhibited a model of set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
in which every set of reals is measurable. This implies that there are no discontinuous linear real functions. Clearly AC does not hold in the model.
Solovay's result shows that it is not necessary to assume that all infinite-dimensional vector spaces admit discontinuous linear maps, and there are schools of analysis which adopt a more constructivist
Constructivism (mathematics)
In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
viewpoint. For example H. G. Garnir, in searching for so-called "dream spaces" (topological vector spaces on which every linear map into a normed space is continuous), was led to adopt ZF + DC + BP (dependent choice is a weakened form and the Baire property is a negation of strong AC) as his axioms to prove the Garnir-Wright closed graph theorem which states, among other things, that any linear map from an F-space
F-space
In functional analysis, an F-space is a vector space V over the real or complex numbers together with a metric d : V × V → R so that...
to a TVS is continuous. Going to the extreme of constructivism, there is Ceitin's theorem, which states that every map is continuous (where this is to be understood in an appropriate framework). Such stances are held by only a small minority of working mathematicians.
The upshot is that it is not possible to obviate the need for AC; it is consistent with set theory without AC that there are no discontinuous linear maps. A corollary is that constructible discontinuous operators such as the derivative cannot be everywhere-defined on a complete space.
Closed operators
Many naturally occurring linear discontinuous operators occur are closedClosed operator
In mathematics, specifically in functional analysis, closed linear operators are an important class of linear operators on Banach spaces. They are more general than bounded operators, and therefore not necessarily continuous, but they still retain nice enough properties that one can define the...
, a class of operators which share some of the features of continuous operators. It makes sense to ask the analogous question about whether all linear operators on a given space are closed. The closed graph theorem
Closed graph theorem
In mathematics, the closed graph theorem is a basic result in functional analysis which characterizes continuous linear operators between Banach spaces in terms of the operator graph.- The closed graph theorem :...
asserts that all everywhere-defined closed operators on a complete domain are continuous, so in the context of discontinuous closed operators, one must allow for operators which are not defined everywhere. Among operators which are not everywhere-defined, one can consider densely-defined operators without loss of generality.
Thus let
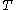be a map 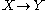with domain 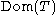. The graph 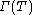of an operator 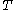which is not everywhere-defined will admit a distinct closure . If the closure of the graph is itself the graph of some operator 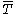, 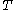is called closable, and 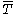is called the closure of 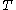.So the right question to ask about linear operators that are densely-defined is whether they are closable. The answer is not necessarily; one can prove that every infinite-dimensional normed space admits a nonclosable linear operator. The proof requires the axiom of choice and so is in general nonconstructive, though again, if X is not complete, there are constructible examples.
In fact, an example of a linear operator whose graph has closure all of X×Y can be given. Such an operator is not closable. Let X be the space of polynomial functions from [0,1] to R and Y the space of polynomial functions from [2,3] to R. They are subspaces of C([0,1]) and C([2,3]) respectively, and so normed spaces. Define an operator T which takes the polynomial function x ↦ p(x) to on [0,1] to the same function on [2,3]. As a consequence of the Stone-Weierstrass theorem
Stone-Weierstrass theorem
In mathematical analysis, the Weierstrass approximation theorem states that every continuous function defined on an interval [a,b] can be uniformly approximated as closely as desired by a polynomial function...
, the graph of this operator is dense in X×Y, so this provides a sort of maximally discontinuous linear map (confer nowhere continuous function). Note that X is not complete here, as must be the case when there is such a constructible map.
Impact for dual spaces
The dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of a topological vector space is the collection of continuous linear maps from the space into the underlying field. Thus the failure of some linear maps to be continuous for infinite-dimensional normed spaces implies that for these spaces, one needs to distinguish the algebraic dual space from the continuous dual space which is then a proper subset. It illustrates the fact that an extra dose of caution is needed in doing analysis on infinite-dimensional spaces as compared to finite-dimensional ones.
Beyond normed spaces
The argument for the existence of discontinuous linear maps on normed spaces can be generalized to all metrisable topological vector spaces, especially to all Fréchet-spaces, but there exist infinite dimensional locally convex topological vector spaces such that every functional is continuous. On the other hand, the Hahn–Banach theoremHahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
, which applies to all locally convex spaces, guarantees the existence of many continuous linear functionals, and so a large dual space. In fact, to every convex set, the Minkowski gauge associates a continuous linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
. The upshot is that spaces with fewer convex sets have fewer functionals, and in the worst case scenario, a space may have no functionals at all other than the zero functional. This is the case for the Lp(R,dx)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
spaces with 0<p<1, from which it follows that these spaces are nonconvex. Note that here is indicated the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on the real line. There are other Lp spaces with 0<p<1 which do have nontrivial dual spaces.
Another such example is the space of real-valued measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
s on the unit interval with quasinorm given by
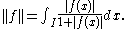
This non-locally convex space has a trivial dual space.
One can consider even more general spaces. For example, the existence of a homomorphism between complete separable metric group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s can also be shown nonconstructively.