F-space
Encyclopedia
In functional analysis
, an F-space is a vector space
V over the real
or complex
numbers together with a metric
d : V × V → R so that
Some authors call these spaces "Fréchet spaces", but usually the term Fréchet space
is reserved for locally convex F-spaces. The metric may or may not necessarily be part of the structure on an F-space; many authors only require that such a space be metrizable in a manner that satisfies the above properties.
s and Fréchet space
s are F-spaces. In particular, a Banach space is an F-space with an additional requirement that .
The Lp spaces
are F-spaces for all p>0 and for p ≥ 1 they are locally convex and thus Fréchet spaces and even Banach spaces.
Example 1 L1/2[0,1] is a F-space. It admits no continuous seminorms and no continuous linear functionals — it has trivial dual space
.
Example 2 Let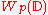
be the space of all complex valued Taylor series
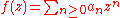
on the unit disc
such that
, then (for 0 are F-spaces under the p-norm
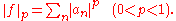
In fact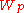
is a quasi-Banach algebra. Moreover, for any 
with 
the map
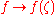
is a bounded linear (multiplicative functional) on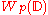
.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, an F-space is a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V over the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
numbers together with a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
d : V × V → R so that
- Scalar multiplication in V is continuous with respect to d and the standard metric on R or C.
- Addition in V is continuous with respect to d.
- The metric is translation-invariant, i.e. d(x+a, y+a) = d(x, y) for all x, y and a in V
- The metric space (V, d) is complete
Some authors call these spaces "Fréchet spaces", but usually the term Fréchet space
Fréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
is reserved for locally convex F-spaces. The metric may or may not necessarily be part of the structure on an F-space; many authors only require that such a space be metrizable in a manner that satisfies the above properties.
Examples
Clearly, all Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s and Fréchet space
Fréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
s are F-spaces. In particular, a Banach space is an F-space with an additional requirement that .
The Lp spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
are F-spaces for all p>0 and for p ≥ 1 they are locally convex and thus Fréchet spaces and even Banach spaces.
Example 1 L1/2[0,1] is a F-space. It admits no continuous seminorms and no continuous linear functionals — it has trivial dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
.
Example 2 Let
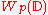be the space of all complex valued Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
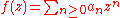
on the unit disc
such that, then (for 0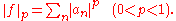In fact
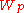is a quasi-Banach algebra. Moreover, for any with the map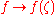is a bounded linear (multiplicative functional) on
.
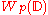