Cayley transform
Encyclopedia
In mathematics
, the Cayley transform, named after Arthur Cayley
, has a cluster of related meanings. As originally described by , the Cayley transform is a mapping between skew-symmetric matrices
and special orthogonal matrices. In complex analysis
, the Cayley transform is a conformal map
ping in which the image of the upper complex half-plane is the unit disk . And in the theory of Hilbert space
s, the Cayley transform is a mapping between linear operators .
, with I the identity matrix, let A be any skew-symmetric matrix
(so that AT = −A). Then I + A is invertible, and the Cayley transform
produces an orthogonal matrix
, Q (so that QTQ = I). The matrix multiplication in the definition of Q above is commutative, so Q can be alternatively defined as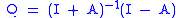
. In fact, Q must have determinant +1, so is special orthogonal. Conversely, let Q be any orthogonal matrix which does not have −1 as an eigenvalue; then
is a skew-symmetric matrix. The condition on Q automatically excludes matrices with determinant −1, but also excludes certain special orthogonal matrices. Some authors use a superscript "c" to denote this transform, writing Q = Ac and A = Qc.
This version of the Cayley transform is its own functional inverse, so that A = (Ac)c and Q = (Qc)c. A slightly different form is also seen , requiring different mappings in each direction (and dropping the superscript notation):
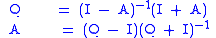
The mappings may also be written with the order of the factors reversed ; however, A always commutes with (μI ± A)−1, so the reordering does not affect the definition.
The 180° rotation matrix, −I, is excluded, though it is the limit as tan θ⁄2 goes to infinity.
In the 3×3 case, we have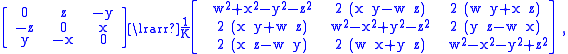
where K = w2 + x2 + y2 + z2, and where w = 1. This we recognize as the rotation matrix corresponding to quaternion
(by a formula Cayley had published the year before), except scaled so that w = 1 instead of the usual scaling so that w2 + x2 + y2 + z2 = 1. Thus vector (x,y,z) is the unit axis of rotation scaled by tan θ⁄2. Again excluded are 180° rotations, which in this case are all Q which are symmetric (so that QT = Q).
matrices by substituting "unitary" for "orthogonal" and "skew-Hermitian
" for "skew-symmetric", the difference being that the transpose (·T) is replaced by the conjugate transpose
(·H). This is consistent with replacing the standard real inner product with the standard complex inner product. In fact, we may extend the definition further with choices of adjoint
other than transpose or conjugate transpose.
Formally, the definition only requires some invertibility, so we can substitute for Q any matrix M whose eigenvalues do not include −1. For example, we have
We remark that A is skew-symmetric (respectively, skew-Hermitian) if and only if Q is orthogonal (respectively, unitary) with no eigenvalue −1.
In complex analysis
, the Cayley transform is a mapping of the complex plane
to itself, given by
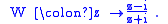
This is a linear fractional transformation, and can be extended to an automorphism
of the Riemann sphere
(the complex plane
augmented with a point at infinity).
Of particular note are the following facts:
is a Hilbert space
, and we can no longer speak of matrices
. However, matrices are merely representations of linear operators, and these we still have. So, generalizing both the matrix mapping and the complex plane mapping, we may define a Cayley transform of operators.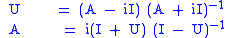
Here the domain of U, dom U, is (A+iI) dom A. See self-adjoint operator for further details.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Cayley transform, named after Arthur Cayley
Arthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
, has a cluster of related meanings. As originally described by , the Cayley transform is a mapping between skew-symmetric matrices
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
and special orthogonal matrices. In complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, the Cayley transform is a conformal map
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
ping in which the image of the upper complex half-plane is the unit disk . And in the theory of Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s, the Cayley transform is a mapping between linear operators .
Matrix map
Among n×n square matrices over the realsReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, with I the identity matrix, let A be any skew-symmetric matrix
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
(so that AT = −A). Then I + A is invertible, and the Cayley transform
produces an orthogonal matrix
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
, Q (so that QTQ = I). The matrix multiplication in the definition of Q above is commutative, so Q can be alternatively defined as
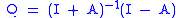. In fact, Q must have determinant +1, so is special orthogonal. Conversely, let Q be any orthogonal matrix which does not have −1 as an eigenvalue; thenis a skew-symmetric matrix. The condition on Q automatically excludes matrices with determinant −1, but also excludes certain special orthogonal matrices. Some authors use a superscript "c" to denote this transform, writing Q = Ac and A = Qc.
This version of the Cayley transform is its own functional inverse, so that A = (Ac)c and Q = (Qc)c. A slightly different form is also seen , requiring different mappings in each direction (and dropping the superscript notation):
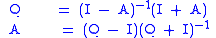
The mappings may also be written with the order of the factors reversed ; however, A always commutes with (μI ± A)−1, so the reordering does not affect the definition.
Examples
In the 2×2 case, we haveThe 180° rotation matrix, −I, is excluded, though it is the limit as tan θ⁄2 goes to infinity.
In the 3×3 case, we have
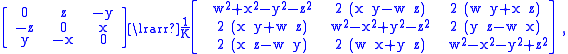
where K = w2 + x2 + y2 + z2, and where w = 1. This we recognize as the rotation matrix corresponding to quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
(by a formula Cayley had published the year before), except scaled so that w = 1 instead of the usual scaling so that w2 + x2 + y2 + z2 = 1. Thus vector (x,y,z) is the unit axis of rotation scaled by tan θ⁄2. Again excluded are 180° rotations, which in this case are all Q which are symmetric (so that QT = Q).
Other matrices
We can extend the mapping to complexComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
matrices by substituting "unitary" for "orthogonal" and "skew-Hermitian
Skew-Hermitian matrix
In linear algebra, a square matrix with complex entries is said to be skew-Hermitian or antihermitian if its conjugate transpose is equal to its negative. That is, the matrix A is skew-Hermitian if it satisfies the relationA^\dagger = -A,\;...
" for "skew-symmetric", the difference being that the transpose (·T) is replaced by the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
(·H). This is consistent with replacing the standard real inner product with the standard complex inner product. In fact, we may extend the definition further with choices of adjoint
Adjoint
In mathematics, the term adjoint applies in several situations. Several of these share a similar formalism: if A is adjoint to B, then there is typically some formula of the type = .Specifically, adjoint may mean:...
other than transpose or conjugate transpose.
Formally, the definition only requires some invertibility, so we can substitute for Q any matrix M whose eigenvalues do not include −1. For example, we have
We remark that A is skew-symmetric (respectively, skew-Hermitian) if and only if Q is orthogonal (respectively, unitary) with no eigenvalue −1.
Conformal map
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, the Cayley transform is a mapping of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
to itself, given by
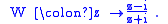
This is a linear fractional transformation, and can be extended to an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
(the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
augmented with a point at infinity).
Of particular note are the following facts:
- W maps the upper half plane of C conformally onto the unit disc of C.
- W maps the real line R injectively into the unit circle T (complex numbers of absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
1). The image of R is T with 1 removed. - W maps the upper imaginary axis i
[0, ∞) bijectivelyBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
onto the half-open interval[−1, +1) . - W maps 0 to −1.
- W maps the point at infinity to 1.
- W maps −i to the point at infinity (so W has a pole at −i).
- W maps −1 to i.
- W maps both 1⁄2(−1 + √3)(−1 + i) and 1⁄2(1 + √3)(1 − i) to themselves.
Operator map
An infinite-dimensional version of an inner product spaceInner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
is a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, and we can no longer speak of matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. However, matrices are merely representations of linear operators, and these we still have. So, generalizing both the matrix mapping and the complex plane mapping, we may define a Cayley transform of operators.
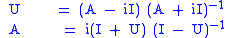
Here the domain of U, dom U, is (A+iI) dom A. See self-adjoint operator for further details.