Normal operator
Encyclopedia
In mathematics
, especially functional analysis
, a normal operator on a complex Hilbert space
(or equivalently in a C* algebra) is a continuous linear operator
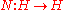
that commutes
with its hermitian adjoint
N*:
Normal operators are important because the spectral theorem holds for them. Today, the class of normal operators is well-understood. Examples of normal operators are
. A compact normal operator
(in particular, a normal operator on a finite-dimensional linear space) is diagonalizable.
Let T be a bounded operator. The following are equivalent.
If N is a normal operator, then N and N* have the same kernel and range. Consequently, the range of N is dense if and only if N is injective. Put in another way, the kernel of a normal operator is the orthogonal complement of its range; thus, the kernel of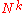
coincides with that of 
for any 
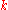. Every generalized eigenvalue of a normal operator is thus genuine. 
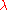is an eigenvalue of a normal operator N if and only if its complex conjugate 
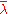is an eigenvalue of 
Eigenvectors of a normal operator corresponding to different eigenvalues are orthogonal, and it stabilizes orthogonal complements to its eigenspaces
. This implies the usual spectral theorem: every normal operator on a finite-dimensional space is diagonalizable by a unitary operator. There is also an infinite dimensional generalization in terms of projection-valued measures. Residual spectrum of a normal operator is empty.
The product of normal operators that commute is again normal; this is nontrivial and follows from Fuglede's theorem
, which states (in a form generalized by Putnam):
The operator norm of a normal operator equals to its numerical radius and spectral radius
.
A normal operator coincides with its Aluthge transform.
on a finite-dimensional real or complex Hilbert space (inner product space) 
stabilizes a subspace 
, then it also stabilizes its orthogonal complement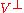 
.
Proof. Denote by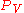
the orthogonal projection onto 
.
Then the orthogonal projection onto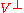
is 
.
The fact that
stabilizes 
can be expressed as
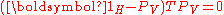, or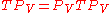 
.
The goal is to show that
.
Since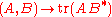
is an inner product on the space of endomorphisms of 
, it is enough to show that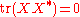 
.
This follows from a direct computation, using properties of the trace
and of orthogonal projections:
,
.
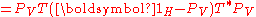
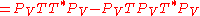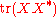
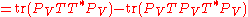
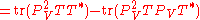
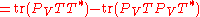
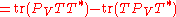
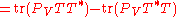
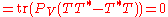This generalizes to compact normal operators in infinite dimensional Hilbert spaces. However, for bounded normal operators orthogonal complement to a stable subspace may not be stable. It follows that such subspaces cannot be spanned by eigenvectors.
. The most important case is when such an algebra is a C*-algebra. A positive element is an example of a normal element.
Here, the existence of the adjoint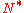
implies that the domain of 
is dense, and the equality implies that the domain of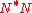 
equals that of 
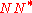, which is not necessarily the case in general.
The spectral theorem still holds for unbounded normal operators, but usually requires a different proof.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, a normal operator on a complex Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
(or equivalently in a C* algebra) is a continuous linear operator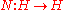that commutes
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
with its hermitian adjoint
Hermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
N*:
Normal operators are important because the spectral theorem holds for them. Today, the class of normal operators is well-understood. Examples of normal operators are
- unitary operatorUnitary operatorIn functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
s: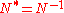
- Hermitian operators (i.e., selfadjoint operators):
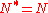; (also, anti-selfadjoint operators: 
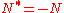) - positive operators:
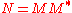
- orthogonal projection operators:
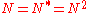
- normal matricesNormal matrixA complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
can be seen as normal operators if one takes the Hilbert space to be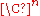
.
Properties
Normal operators are characterized by the spectral theoremSpectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
. A compact normal operator
Compact operator on Hilbert space
In functional analysis, compact operators on Hilbert spaces are a direct extension of matrices: in the Hilbert spaces, they are precisely the closure of finite-rank operators in the uniform operator topology. As such, results from matrix theory can sometimes be extended to compact operators using...
(in particular, a normal operator on a finite-dimensional linear space) is diagonalizable.
Let T be a bounded operator. The following are equivalent.
- T is normal.
- T* is normal.
- ||Tx|| = ||T*x|| for all x (use
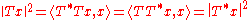). - The selfadjoint and anti-selfadjoint parts of T commute.
If N is a normal operator, then N and N* have the same kernel and range. Consequently, the range of N is dense if and only if N is injective. Put in another way, the kernel of a normal operator is the orthogonal complement of its range; thus, the kernel of
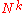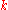coincides with that of for any . Every generalized eigenvalue of a normal operator is thus genuine. 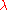is an eigenvalue of a normal operator N if and only if its complex conjugate 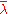is an eigenvalue of Eigenvectors of a normal operator corresponding to different eigenvalues are orthogonal, and it stabilizes orthogonal complements to its eigenspaces. This implies the usual spectral theorem: every normal operator on a finite-dimensional space is diagonalizable by a unitary operator. There is also an infinite dimensional generalization in terms of projection-valued measures. Residual spectrum of a normal operator is empty.
The product of normal operators that commute is again normal; this is nontrivial and follows from Fuglede's theorem
Fuglede's theorem
In mathematics, Fuglede's theorem is a result in operator theory, named after Bent Fuglede.- The result :Theorem Let T and N be bounded operators on a complex Hilbert space with N being normal. If TN = NT, then TN* = N*T, where N* denotes the adjoint of N.Normality of N is necessary, as is seen by...
, which states (in a form generalized by Putnam):
- If
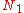and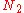 
are normal operators and if A is a bounded linear operator such that 
, then 
.
The operator norm of a normal operator equals to its numerical radius and spectral radius
Spectral radius
In mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
.
A normal operator coincides with its Aluthge transform.
Properties in finite-dimensional case
If a normal operator on a finite-dimensional real or complex Hilbert space (inner product space) stabilizes a subspace , then it also stabilizes its orthogonal complement 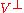.Proof. Denote by
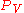the orthogonal projection onto .Then the orthogonal projection onto
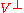is .The fact that
stabilizes can be expressed as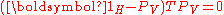, or 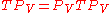.The goal is to show that
.Since
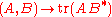is an inner product on the space of endomorphisms of , it is enough to show that 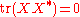.This follows from a direct computation, using properties of the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
and of orthogonal projections:
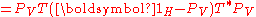
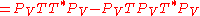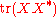
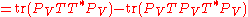
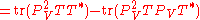
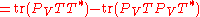
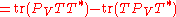
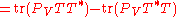
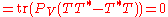,.This generalizes to compact normal operators in infinite dimensional Hilbert spaces. However, for bounded normal operators orthogonal complement to a stable subspace may not be stable. It follows that such subspaces cannot be spanned by eigenvectors.
Normal elements
The notion of normal operators generalizes to an involutive algebra; namely, an element x of an involutive algebra is said to be normal if. The most important case is when such an algebra is a C*-algebra. A positive element is an example of a normal element.Unbounded normal operators
The definition of normal operators naturally generalizes to some class of unbounded operators. Explicitly, a closed operator N is said to be normal ifHere, the existence of the adjoint
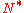implies that the domain of is dense, and the equality implies that the domain of 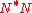equals that of 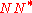, which is not necessarily the case in general.The spectral theorem still holds for unbounded normal operators, but usually requires a different proof.
Generalization
The success of the theory of normal operators led to several attempts for generalization by weakening the commutativity requirement. Classes of operators that include normal operators are (in order of inclusion)- Quasinormal operatorQuasinormal operatorIn operator theory, quasinormal operators is a class of bounded operators defined by weakening the requirements of a normal operator.Every quasinormal operator is a subnormal operator...
s - Subnormal operatorSubnormal operatorIn mathematics, especially operator theory, subnormal operators are bounded operators on a Hilbert space defined by weakening the requirements for normal operators. Some examples of subnormal operators are isometries and Toeplitz operators with analytic symbols.-Definition:Let H be a Hilbert space...
s - Hyponormal operatorHyponormal operatorIn mathematics, especially operator theory, a hyponormal operator is a generalization of a normal operator. In general, a bounded linear operator T on a complex Hilbert space H is said to be p-hyponormal In mathematics, especially operator theory, a hyponormal operator is a generalization of a...
s - Paranormal operatorParanormal operatorIn mathematics, especially operator theory, a paranormal operator is a generalization of a normal operator. More precisely, a bounded linear operator T on a complex Hilbert space H is said to be paranormal if:for every unit vector x in H....
s - Normaloids