
Subnormal operator
Encyclopedia
In mathematics
, especially operator theory
, subnormal operators are bounded operator
s on a Hilbert space
defined by weakening the requirements for normal operator
s. Some examples of subnormal operators are isometries
and Toeplitz operator
s with analytic symbols.
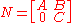
for some bounded operators
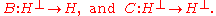
s. A unitary operator is an isometry with dense
range
. Consider now an isometry A whose range is not necessarily dense. A concrete example of such is the unilateral shift, which is not normal. But A is subnormal and this can be shown explicitly. Define an operator U on

by
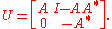
Direct calculation shows that U is unitary, therefore a normal extension of A. The operator U is called the unitary dilation
of the isometry A.
if A commutes with A*A. A normal operator is thus quasinormal; the converse is not true. A counter example is given, as above, by the unilateral shift. Therefore the family of normal operators is a proper subset of both quasinormal and subnormal operators. A natural question is how are the quasinormal and subnormal operators related.
We will show that a quasinormal operator is necessarily subnormal but not vice versa. Thus the normal operators is a proper subfamily of quasinormal operators, which in turn are contained by the subnormal operators. To argue the claim that a quasinormal operator is subnormal, recall the following property of quasinormal operators:
Fact: A bounded operator A is quasinormal if and only if in its polar decomposition A = UP, the partial isometry U and positive operator P commute.
Given a quasinormal A, the idea is to construct dilations for U and P in a sufficiently nice way so everything commutes. Suppose for the moment that U is an isometry. Let V be the unitary dilation of U,
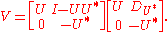
Define
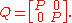
The operator N = VQ is clearly an extension of A. We show it is a normal extension via direct calculation. Unitarity of V means
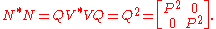
On the other hand,
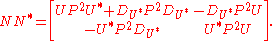
Because UP = PU and P is self adjoint, we have U*P = PU* and DU*P = DU*P. Comparing entries then shows N is normal. This proves quasinormality implies subnormality.
For a counter example that shows the converse is not true, consider again the unilateral shift A. The operator B = A + s for some scalar s remains subnormal. But if B is quasinormal, a straightforward calculation shows that A*A = AA*, which is a contradiction.
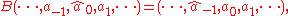
where ˆ denotes the zero-th position. B can be expressed in terms of the operator matrix
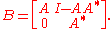
Another normal extension is given by the unitary dilation B' of A defined above:
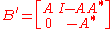
whose action is described by

One can show that if two operators B1 and B2 are minimal extensions on K1 and K2, respectively, then there exists a unitary operator
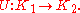
Also, the following interwining relationship holds:

This can be shown constructively. Consider the set S consisting of vectors of the following form:
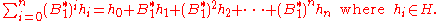
Let K' ⊂ K1 be the subspace that is the closure of the linear span of S. By definition, K' is invariant under B1* and contains H. The normality of B1 and the assumption that H is invariant under B1 imply K' is invariant under B1. Therefore K' = K1. The Hilbert space K2 can be identified in exactly the same way. Now we define the operator U as follows:
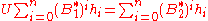
Because
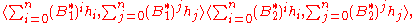
, the operator U is unitary. Direct computation also shows (the assumption that both B1 and B2 are extensions of A are needed here)
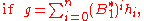

When B1 and B2 are not assumed to be minimal, the same calculation shows that above claim holds verbatim with U being a partial isometry
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, subnormal operators are bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
s on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
defined by weakening the requirements for normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
s. Some examples of subnormal operators are isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
and Toeplitz operator
Toeplitz operator
In operator theory, a Toeplitz operator is the compression of a multiplication operator on the circle to the Hardy space.- Details :Let S1 be the circle, with the standard Lebesgue measure, and L2 be the Hilbert space of square-integrable functions. A bounded measurable function g on S1 defines a...
s with analytic symbols.
Definition
Let H be a Hilbert space. A bounded operator A on H is said to be subnormal if A has a normal extension. In other words, A is subnormal if there exists a Hilbert space K such that H can be embedded in K and there exists a normal operator N of the form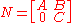
for some bounded operators
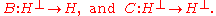
Normal operators
Every normal operator is subnormal by definition, but the converse is not true in general. A simple class of examples can be obtained by weakening the properties of unitary operatorUnitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
s. A unitary operator is an isometry with dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
. Consider now an isometry A whose range is not necessarily dense. A concrete example of such is the unilateral shift, which is not normal. But A is subnormal and this can be shown explicitly. Define an operator U on

by
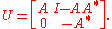
Direct calculation shows that U is unitary, therefore a normal extension of A. The operator U is called the unitary dilation
Unitary dilation
In operator theory, a dilation of an operator T on a Hilbert space H is an operator on a larger Hilbert space K , whose restriction to H is T....
of the isometry A.
Quasinormal operators
An operator A is said to be quasinormalQuasinormal operator
In operator theory, quasinormal operators is a class of bounded operators defined by weakening the requirements of a normal operator.Every quasinormal operator is a subnormal operator...
if A commutes with A*A. A normal operator is thus quasinormal; the converse is not true. A counter example is given, as above, by the unilateral shift. Therefore the family of normal operators is a proper subset of both quasinormal and subnormal operators. A natural question is how are the quasinormal and subnormal operators related.
We will show that a quasinormal operator is necessarily subnormal but not vice versa. Thus the normal operators is a proper subfamily of quasinormal operators, which in turn are contained by the subnormal operators. To argue the claim that a quasinormal operator is subnormal, recall the following property of quasinormal operators:
Fact: A bounded operator A is quasinormal if and only if in its polar decomposition A = UP, the partial isometry U and positive operator P commute.
Given a quasinormal A, the idea is to construct dilations for U and P in a sufficiently nice way so everything commutes. Suppose for the moment that U is an isometry. Let V be the unitary dilation of U,
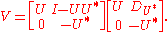
Define
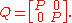
The operator N = VQ is clearly an extension of A. We show it is a normal extension via direct calculation. Unitarity of V means
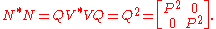
On the other hand,
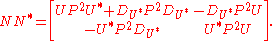
Because UP = PU and P is self adjoint, we have U*P = PU* and DU*P = DU*P. Comparing entries then shows N is normal. This proves quasinormality implies subnormality.
For a counter example that shows the converse is not true, consider again the unilateral shift A. The operator B = A + s for some scalar s remains subnormal. But if B is quasinormal, a straightforward calculation shows that A*A = AA*, which is a contradiction.
Non-uniqueness of normal extensions
Given a subnormal operator A, its normal extension B is not unique. For example, let A be the unilateral shift, on l2(N). One normal extension is the bilateral shift B on l2(Z) defined by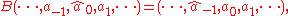
where ˆ denotes the zero-th position. B can be expressed in terms of the operator matrix
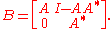
Another normal extension is given by the unitary dilation B' of A defined above:
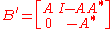
whose action is described by

Minimality
Thus one is interested in the normal extension that is, in some sense, smallest. More precisely, a normal operator B acting on a Hilbert space K is said to be a minimal extension of a subnormal A if K' ⊂ K is a reducing subspace of B and H ⊂ K' , then K' = K. (A subspace is a reducing subspace of B if it is invariant under both B and B*.)One can show that if two operators B1 and B2 are minimal extensions on K1 and K2, respectively, then there exists a unitary operator
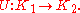
Also, the following interwining relationship holds:

This can be shown constructively. Consider the set S consisting of vectors of the following form:
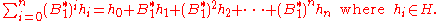
Let K' ⊂ K1 be the subspace that is the closure of the linear span of S. By definition, K' is invariant under B1* and contains H. The normality of B1 and the assumption that H is invariant under B1 imply K' is invariant under B1. Therefore K' = K1. The Hilbert space K2 can be identified in exactly the same way. Now we define the operator U as follows:
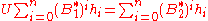
Because
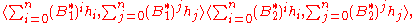
, the operator U is unitary. Direct computation also shows (the assumption that both B1 and B2 are extensions of A are needed here)
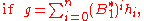

When B1 and B2 are not assumed to be minimal, the same calculation shows that above claim holds verbatim with U being a partial isometry
Partial isometry
In functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...
.

