
Quasinormal operator
Encyclopedia
In operator theory
, quasinormal operators is a class of bounded operators defined by weakening the requirements of a normal operator
.
Every quasinormal operator is a subnormal operator
. Every quasinormal operator on a finite-dimensional Hilbert space is normal.

Let A = UP be the polar decomposition of A. If A is quasinormal, then UP = PU. To see this, notice that
the positive factor P in the polar decomposition is of the form (A*A)½, the unique positive square root of A*A. Quasinormality means A commutes with A*A. As a consequence of the continuous functional calculus
for self adjoint operators, A commutes with P = (A*A)½ also, i.e.

So UP = PU on the range of P. On the other hand, if h ∈ H lies in kernel of P, clearly UP h = 0. But PU h = 0 as well. because U is a partial isometry
whose initial space is closure of range P. Finally, the self-adjointness of P implies that H is the direct sum of its range and kernel. Thus the argument given proves UP = PU on all of H.
On the other hand, one can readily verify that if UP = PU, then A must be quasinormal. Thus the operator A is quasinormal if and only if UP = PU.
When H is finite dimensional, every quasinormal operator A is normal. This is because that in the finite dimensional case, the partial isometry U in the polar decomposition A = UP can be taken to be unitary. This then gives
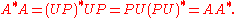
In general, a partial isometry may not be extendable to a unitary operator and therefore a quasinormal operator need not be normal. For example, consider the unilateral shift T. T is quasinormal because T*T is the identity operator. But T is clearly not normal.
. Every normal operator A is obtained by integrating the identity function with respect to a spectral measure E = {EB} on the spectrum of A, σ(A):

For any Borel set B ⊂ σ(A), the projection EB commutes with A and therefore the range of EB is an invariant subpsace of A.
The above can be extended directly to quasinormal operators. To say A commutes with A*A is to say that A commutes with (A*A)½. But this implies that A commutes with any projection EB in the spectral measure of (A*A)½, which proves the invariant subspace claim. In fact, one can conclude something stronger. The range of EB is actually a reducing subspace of A, i.e. its orthogonal complement is also invariant under A.
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, quasinormal operators is a class of bounded operators defined by weakening the requirements of a normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
.
Every quasinormal operator is a subnormal operator
Subnormal operator
In mathematics, especially operator theory, subnormal operators are bounded operators on a Hilbert space defined by weakening the requirements for normal operators. Some examples of subnormal operators are isometries and Toeplitz operators with analytic symbols.-Definition:Let H be a Hilbert space...
. Every quasinormal operator on a finite-dimensional Hilbert space is normal.
Definition
Let A be a bounded operator on a Hilbert space H, then A is said to be quasinormal if A commutes with A*A, i.e.
Properties
A normal operator is necessarily quasinormal.Let A = UP be the polar decomposition of A. If A is quasinormal, then UP = PU. To see this, notice that
the positive factor P in the polar decomposition is of the form (A*A)½, the unique positive square root of A*A. Quasinormality means A commutes with A*A. As a consequence of the continuous functional calculus
Continuous functional calculus
In mathematics, the continuous functional calculus of operator theory and C*-algebra theory allows applications of continuous functions to normal elements of a C*-algebra. More precisely,Theorem...
for self adjoint operators, A commutes with P = (A*A)½ also, i.e.

So UP = PU on the range of P. On the other hand, if h ∈ H lies in kernel of P, clearly UP h = 0. But PU h = 0 as well. because U is a partial isometry
Partial isometry
In functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...
whose initial space is closure of range P. Finally, the self-adjointness of P implies that H is the direct sum of its range and kernel. Thus the argument given proves UP = PU on all of H.
On the other hand, one can readily verify that if UP = PU, then A must be quasinormal. Thus the operator A is quasinormal if and only if UP = PU.
When H is finite dimensional, every quasinormal operator A is normal. This is because that in the finite dimensional case, the partial isometry U in the polar decomposition A = UP can be taken to be unitary. This then gives
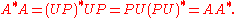
In general, a partial isometry may not be extendable to a unitary operator and therefore a quasinormal operator need not be normal. For example, consider the unilateral shift T. T is quasinormal because T*T is the identity operator. But T is clearly not normal.
Quasinormal invariant subspaces
It is not known that, in general, whether a bounded operator A on a Hilbert space H has a nontrivial invariant subspace. However, when A is normal, an affirmative answer is given by the spectral theoremSpectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
. Every normal operator A is obtained by integrating the identity function with respect to a spectral measure E = {EB} on the spectrum of A, σ(A):

For any Borel set B ⊂ σ(A), the projection EB commutes with A and therefore the range of EB is an invariant subpsace of A.
The above can be extended directly to quasinormal operators. To say A commutes with A*A is to say that A commutes with (A*A)½. But this implies that A commutes with any projection EB in the spectral measure of (A*A)½, which proves the invariant subspace claim. In fact, one can conclude something stronger. The range of EB is actually a reducing subspace of A, i.e. its orthogonal complement is also invariant under A.

