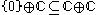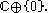Partial isometry
Encyclopedia
In functional analysis
a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction
of W to the orthogonal complement of its kernel
is an isometry
. We call the orthogonal complement of the kernel of W the initial subspace of W, and the range of W is called the final subspace of W.
Any unitary operator
on H is a partial isometry with initial and final subspaces being all of H.
For example, In the two-dimensional complex Hilbert space C2 the matrix
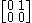
is a partial isometry with initial subspace
and final subspace
The concept of partial isometry can be defined in other equivalent ways. If U is an isometric map defined on a closed subset H1 of a Hilbert space H then we can define an extension W of U to all of H by the condition that W be zero on the orthogonal complement of H1. Thus a partial isometry is also sometimes defined as a closed partially defined isometric map.
Partial isometries are also characterized by the condition that W W* or W* W is a projection. In that case, both W W* and W* W are projections (of course, since orthogonal projections are self-adjoint, each orthogonal projection is a partial isometry). This allows us to define partial isometry in any C*-algebra as follows:
If A is a C*-algebra, an element W in A is a partial isometry if and only if
W W* or W* W is a projection (self-adjoint idempotent) in A. In that case W W* and W* W are both projections, and
When A is an operator algebra
, the ranges of these projections are the initial and final subspaces of W respectively.
It is not hard to show that partial isometries are characterised by the equation
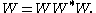
A pair of projections one of which is the initial projection of a partial isometry and the other a final projection of the same isometry are said to be equivalent. This is indeed an equivalence relation
and it plays an important role in K-theory
for C*-algebras, and in the Murray-von Neumann theory of projections in a von Neumann algebra
.
Partial isometries (and projections) can be defined in the more abstract setting of a semigroup with involution
; the definition concides with the one herein.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction
Restriction
Restriction may refer to:* Restriction , an aspect of a mathematical function* Restrictions , an album by Cactus* Restriction enzyme, a type of enzyme that cleaves genetic material...
of W to the orthogonal complement of its kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
is an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
. We call the orthogonal complement of the kernel of W the initial subspace of W, and the range of W is called the final subspace of W.
Any unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
on H is a partial isometry with initial and final subspaces being all of H.
For example, In the two-dimensional complex Hilbert space C2 the matrix
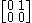
is a partial isometry with initial subspace
and final subspace
The concept of partial isometry can be defined in other equivalent ways. If U is an isometric map defined on a closed subset H1 of a Hilbert space H then we can define an extension W of U to all of H by the condition that W be zero on the orthogonal complement of H1. Thus a partial isometry is also sometimes defined as a closed partially defined isometric map.
Partial isometries are also characterized by the condition that W W* or W* W is a projection. In that case, both W W* and W* W are projections (of course, since orthogonal projections are self-adjoint, each orthogonal projection is a partial isometry). This allows us to define partial isometry in any C*-algebra as follows:
If A is a C*-algebra, an element W in A is a partial isometry if and only if
W W* or W* W is a projection (self-adjoint idempotent) in A. In that case W W* and W* W are both projections, and
- W*W is called the initial projection of W.
- W W* is called the final projection of W.
When A is an operator algebra
Operator algebra
In functional analysis, an operator algebra is an algebra of continuous linear operators on a topological vector space with the multiplication given by the composition of mappings...
, the ranges of these projections are the initial and final subspaces of W respectively.
It is not hard to show that partial isometries are characterised by the equation
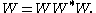
A pair of projections one of which is the initial projection of a partial isometry and the other a final projection of the same isometry are said to be equivalent. This is indeed an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
and it plays an important role in K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
for C*-algebras, and in the Murray-von Neumann theory of projections in a von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
.
Partial isometries (and projections) can be defined in the more abstract setting of a semigroup with involution
Semigroup with involution
In mathematics, in semigroup theory, an involution in a semigroup is a transformation of the semigroup which is its own inverse and which is an anti-automorphism of the semigroup. A semigroup in which an involution is defined is called a semigroup with involution...
; the definition concides with the one herein.