Isometry
Encyclopedia
In mathematics
, an isometry is a distance
-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent
.
Isometries are often used in constructions where one space is embedded
in another space. For instance, the completion of a metric space M involves an isometry from M into M, a quotient set of the space of Cauchy sequence
s on M. The original space M is thus isometrically isomorphic
to a subspace of a complete metric space, and it is usually identified with this subspace. Other embedding constructions show that every metric space is isometrically isomorphic to a closed subset
of some normed vector space
and that every complete metric space is isometrically isomorphic to a closed subset of some Banach space
.
An isometric surjective linear operator on a Hilbert space is called a unitary operator
.
Let X and Y be metric space
s with metrics dX and dY. A map
ƒ : X → Y is called an isometry or distance preserving if for any a,b ∈ X one has
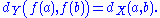
An isometry is automatically injective. Clearly, every isometry between metric spaces is a topological embedding.
A global isometry, isometric isomorphism or congruence mapping is a bijective isometry.
Two metric spaces X and Y are called isometric if there is a bijective isometry from X to Y. The set of bijective isometries from a metric space to itself forms a group
with respect to function composition
, called the isometry group
.
There is also the weaker notion of path isometry or arcwise isometry:
A path isometry or arcwise isometry is a map which preserves the lengths of curves (not necessarily bijective).
This is often called just isometry and one should determine from context which one is intended.
s V and W, a linear isometry is a linear map f : V → W that preserves the norms: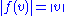
for all v in V. Linear isometries are distance-preserving maps in the above sense. They are global isometries if and only if they are surjective.
By the Mazur-Ulam theorem
, any isometry of normed vector spaces over R is affine
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an isometry is a distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
.
Isometries are often used in constructions where one space is embedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
in another space. For instance, the completion of a metric space M involves an isometry from M into M, a quotient set of the space of Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
s on M. The original space M is thus isometrically isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to a subspace of a complete metric space, and it is usually identified with this subspace. Other embedding constructions show that every metric space is isometrically isomorphic to a closed subset
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
of some normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
and that every complete metric space is isometrically isomorphic to a closed subset of some Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
.
An isometric surjective linear operator on a Hilbert space is called a unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
.
Definitions
The notion of isometry comes in two main flavors: global isometry and a weaker notion path isometry or arcwise isometry. Both are often called just isometry and one should determine from context which one is intended.Let X and Y be metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s with metrics dX and dY. A map
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
ƒ : X → Y is called an isometry or distance preserving if for any a,b ∈ X one has
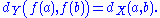
An isometry is automatically injective. Clearly, every isometry between metric spaces is a topological embedding.
A global isometry, isometric isomorphism or congruence mapping is a bijective isometry.
Two metric spaces X and Y are called isometric if there is a bijective isometry from X to Y. The set of bijective isometries from a metric space to itself forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
with respect to function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, called the isometry group
Isometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
.
There is also the weaker notion of path isometry or arcwise isometry:
A path isometry or arcwise isometry is a map which preserves the lengths of curves (not necessarily bijective).
This is often called just isometry and one should determine from context which one is intended.
Examples
- Any reflectionReflection (mathematics)In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
, translationTranslation (geometry)In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
and rotationRotationA rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
is a global isometry on Euclidean spaces. See also Euclidean group.
- The map R
R defined by 
is a path isometry but not an isometry.
- The isometric linear maps from Cn to itself are the unitary matrices.
Linear isometry
Given two normed vector spaceNormed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
s V and W, a linear isometry is a linear map f : V → W that preserves the norms:
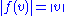
for all v in V. Linear isometries are distance-preserving maps in the above sense. They are global isometries if and only if they are surjective.
By the Mazur-Ulam theorem
Mazur-Ulam theorem
In mathematics, the Mazur–Ulam theorem states that if V and W are normed spaces over R and the mappingf\colon V\to Wis a surjective isometry, then f is affine....
, any isometry of normed vector spaces over R is affine
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
.
Generalizations
- Given a positive real number ε, an ε-isometry or almost isometry (also called a HausdorffFelix HausdorffFelix Hausdorff was a Jewish German mathematician who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, function theory, and functional analysis.-Life:Hausdorff studied at the University of Leipzig,...
approximation) is a map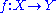
between metric spaces such that
- for x,x′ ∈ X one has |dY(ƒ(x),ƒ(x′))−dX(x,x′)| < ε, and
- for any point y ∈ Y there exists a point x ∈ X with dY(y,ƒ(x)) < ε
- That is, an ε-isometry preserves distances to within ε and leaves no element of the codomain further than ε away from the image of an element of the domain. Note that ε-isometries are not assumed to be continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
.
- Quasi-isometryQuasi-isometryIn mathematics, a quasi-isometry is a means to compare the large-scale structure of metric spaces. The concept is especially important in Gromov's geometric group theory.-Definition:...
is yet another useful generalization.
See also
- Isometric projectionIsometric projectionIsometric projection is a method for visually representing three-dimensional objects in two dimensions in technical and engineering drawings...
- Congruence (geometry)Congruence (geometry)In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
- Euclidean plane isometryEuclidean plane isometryIn geometry, a Euclidean plane isometry is an isometry of the Euclidean plane, or more informally, a way of transforming the plane that preserves geometrical properties such as length...
- 3D isometries that leave the origin fixed
- Space groupSpace groupIn mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
- Involution
- Isometries in physics
- Isometry groupIsometry groupIn mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
- Homeomorphism groupHomeomorphism groupIn mathematics, particularly topology, the homeomorphism group of a topological space is the group consisting of all homeomorphisms from the space to itself with function composition as the group operation. Homeomorphism groups are very important in the theory of topological spaces and in general...
- Partial isometryPartial isometryIn functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...