
Quasi-isometry
Encyclopedia
In mathematics
, a quasi-isometry is a means to compare the large-scale structure of metric space
s. The concept is especially important in Gromov's geometric group theory
.
(not necessarily continuous
). f is called a quasi-isometry if there exist constants A≥1 and B≥0 such that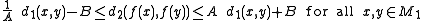
and a constant C≥0 such that to every u in M2 there exists x in M1 with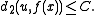
The spaces M1 and M2 are called quasi-isometric if there exists a quasi-isometry f : M1→M2.
Any two finite or bounded metric spaces are quasi-isometric.
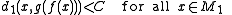
and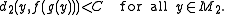
Since the identity map
is a quasi-isometry, and the composition of two quasi-isometries is a quasi-isometry, we see that the relation of being quasi-isometric is an equivalence relation
on the class of metric spaces.
S of a finitely generated group
G, we can form the corresponding Cayley graph
of S and G. This graph becomes a metric space if we declare the length of each edge to be 1. Taking a different finite generating set T results in a different graph and a different metric space, however the two spaces are quasi-isometric. This quasi-isometry class is thus an invariant
of the group G. Any property of metric spaces that only depends on a space's quasi-isometry class immediately yields another invariant of groups, opening the field of group theory to geometric methods.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quasi-isometry is a means to compare the large-scale structure of metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s. The concept is especially important in Gromov's geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
.
Definition
Suppose (M1,d1) and (M2,d2) are metric spaces, and f : M1→M2 is a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
(not necessarily continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
). f is called a quasi-isometry if there exist constants A≥1 and B≥0 such that
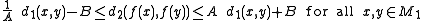
and a constant C≥0 such that to every u in M2 there exists x in M1 with
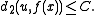
The spaces M1 and M2 are called quasi-isometric if there exists a quasi-isometry f : M1→M2.
Examples
The map f : Zn→Rn which sends every n-tuple of integers to itself is a quasi-isometry (using the Euclidean metric on Zn and Rn).Any two finite or bounded metric spaces are quasi-isometric.
First properties
If f : M1→M2 is a quasi-isometry, then there exists a quasi-isometry g : M2→M1 and a constant C≥0 such that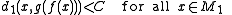
and
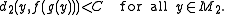
Since the identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
is a quasi-isometry, and the composition of two quasi-isometries is a quasi-isometry, we see that the relation of being quasi-isometric is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the class of metric spaces.
Use in geometric group theory
Given a finite generating setGenerating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
S of a finitely generated group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G, we can form the corresponding Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of S and G. This graph becomes a metric space if we declare the length of each edge to be 1. Taking a different finite generating set T results in a different graph and a different metric space, however the two spaces are quasi-isometric. This quasi-isometry class is thus an invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
of the group G. Any property of metric spaces that only depends on a space's quasi-isometry class immediately yields another invariant of groups, opening the field of group theory to geometric methods.

