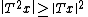Paranormal operator
Encyclopedia
In mathematics
, especially operator theory
, a paranormal operator is a generalization of a normal operator
. More precisely, a bounded linear operator T on a complex Hilbert space
H is said to be paranormal if:
for every unit vector x in H.
The class of paranormal operators was introduced by V. Istratescu in 1960s, though the term "paranormal" is probably due to Furuta.
Every hyponormal operator
(in particular, a subnormal operator
, a quasinormal operator
and a normal operator) is paranormal. If T is a paranormal, then Tn is paranormal. On the other hand, Halmos
gave an example of a hyponormal operator T such that T2 isn't hyponormal. Consequently, not every paranormal operator is hyponormal.
A compact
paranormal operator is normal.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, a paranormal operator is a generalization of a normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
. More precisely, a bounded linear operator T on a complex Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H is said to be paranormal if:
for every unit vector x in H.
The class of paranormal operators was introduced by V. Istratescu in 1960s, though the term "paranormal" is probably due to Furuta.
Every hyponormal operator
Hyponormal operator
In mathematics, especially operator theory, a hyponormal operator is a generalization of a normal operator. In general, a bounded linear operator T on a complex Hilbert space H is said to be p-hyponormal In mathematics, especially operator theory, a hyponormal operator is a generalization of a...
(in particular, a subnormal operator
Subnormal operator
In mathematics, especially operator theory, subnormal operators are bounded operators on a Hilbert space defined by weakening the requirements for normal operators. Some examples of subnormal operators are isometries and Toeplitz operators with analytic symbols.-Definition:Let H be a Hilbert space...
, a quasinormal operator
Quasinormal operator
In operator theory, quasinormal operators is a class of bounded operators defined by weakening the requirements of a normal operator.Every quasinormal operator is a subnormal operator...
and a normal operator) is paranormal. If T is a paranormal, then Tn is paranormal. On the other hand, Halmos
Paul Halmos
Paul Richard Halmos was a Hungarian-born American mathematician who made fundamental advances in the areas of probability theory, statistics, operator theory, ergodic theory, and functional analysis . He was also recognized as a great mathematical expositor.-Career:Halmos obtained his B.A...
gave an example of a hyponormal operator T such that T2 isn't hyponormal. Consequently, not every paranormal operator is hyponormal.
A compact
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
paranormal operator is normal.