Normal matrix
Encyclopedia
A complex
square matrix
A is a normal matrix if
where A* is the conjugate transpose
of A. That is, a matrix is normal if it commutes with its conjugate transpose.
If A is a real
matrix, then A*=AT. Hence, the matrix is normal if ATA = AAT.
Normality is a convenient test for diagonalizability: every normal matrix can be converted to a diagonal matrix by a unitary transform, and every matrix which can be made diagonal by a unitary transform is also normal, but finding the desired transform requires much more work than simply testing to see whether the matrix is normal.
The concept of normal matrices can be extended to normal operator
s on infinite dimensional Hilbert space
s and to normal elements in C*-algebras. As in the matrix case, normality means commutativity is preserved, to the extent possible, in the noncommutative setting. This makes normal operators, and normal elements of C*-algebras, more amenable to analysis.
matrices are normal. Likewise, among real matrices, all orthogonal
, symmetric, and skew-symmetric
matrices are normal.
However, it is not the case that all normal matrices are either unitary or (skew-)Hermitian. As an example, the matrix
is normal because
The matrix A is neither unitary, Hermitian, nor skew-Hermitian.
The sum or product of two normal matrices is not necessarily normal. If they commute, however, then this is true.
If A is both a triangular matrix
and a normal matrix, then A is diagonal
. This can be seen by looking at the diagonal entries of A*A and AA*, where A is a normal, triangular matrix.
applies: a matrix A is normal if and only if it can be represented by a diagonal matrix
Λ and a unitary matrix U by the formula
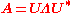
where
The entries λ of diagonal matrix Λ are the eigenvalues of A, and the columns of U are the eigenvectors of A. The matching eigenvalues in Λ come in the same order as the eigenvectors are ordered as columns of U.
Another way of stating the spectral theorem
is to say that normal matrices are precisely those matrices that can be represented by a diagonal matrix with respect to a properly chosen orthonormal basis
of Cn. Phrased differently: a matrix is normal if and only if its eigenspaces span Cn and are pairwise orthogonal with respect to the standard inner product of Cn.
The spectral theorem for normal matrices can be seen as a special case of the more general result which holds for all square matrices: Schur decomposition
. In fact, let A be a square matrix. Then by Schur decomposition it is unitary similar to a upper-triangular matrix, say, B. If A is normal, so is B. But then B must be diagonal, for, as noted above, a normal upper-triangular matrix is diagonal.
The spectral theorem permits the classification of normal matrices in terms of their spectra. For example, a normal matrix is unitary if and only if its spectrum is contained in the unit circle of the complex plane. Also, a normal matrix is self-adjoint
if and only if its spectrum consists of reals.
In general, the sum or product of two normal matrices need not be normal. However, there is a special case: if A and B are normal with AB = BA, then both AB and A + B are also normal. Furthermore the two are simultaneously diagonalizable, that is: both A and B are made diagonal by the same unitary matrix U. Both UAU* and UBU* are diagonal matrices. In this special case, the columns of U* are eigenvectors of both A and B and form an orthonormal basis in Cn.
Some but not all of the above generalize to normal operators on infinite-dimensional Hilbert spaces. For example, a bounded operator satisfying (9) is only quasinormal
.
The operator norm of a normal matrix N equals the spectral
and numerical radii of N. (This fact generalizes to normal operator
s.) Explicitly, this means: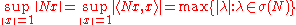
(As a special case, the complex numbers may be embedded in the normal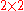
real matrices by the mapping 
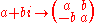, which preserves addition and multiplication. It is easy to check that this embedding respects all of the above analogies.)
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
square matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A is a normal matrix if
where A* is the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of A. That is, a matrix is normal if it commutes with its conjugate transpose.
If A is a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
matrix, then A*=AT. Hence, the matrix is normal if ATA = AAT.
Normality is a convenient test for diagonalizability: every normal matrix can be converted to a diagonal matrix by a unitary transform, and every matrix which can be made diagonal by a unitary transform is also normal, but finding the desired transform requires much more work than simply testing to see whether the matrix is normal.
The concept of normal matrices can be extended to normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
s on infinite dimensional Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s and to normal elements in C*-algebras. As in the matrix case, normality means commutativity is preserved, to the extent possible, in the noncommutative setting. This makes normal operators, and normal elements of C*-algebras, more amenable to analysis.
Special cases
Among complex matrices, all unitary, Hermitian, and skew-HermitianSkew-Hermitian matrix
In linear algebra, a square matrix with complex entries is said to be skew-Hermitian or antihermitian if its conjugate transpose is equal to its negative. That is, the matrix A is skew-Hermitian if it satisfies the relationA^\dagger = -A,\;...
matrices are normal. Likewise, among real matrices, all orthogonal
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
, symmetric, and skew-symmetric
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
matrices are normal.
However, it is not the case that all normal matrices are either unitary or (skew-)Hermitian. As an example, the matrix
is normal because
The matrix A is neither unitary, Hermitian, nor skew-Hermitian.
The sum or product of two normal matrices is not necessarily normal. If they commute, however, then this is true.
If A is both a triangular matrix
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
and a normal matrix, then A is diagonal
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
. This can be seen by looking at the diagonal entries of A*A and AA*, where A is a normal, triangular matrix.
Consequences
The concept of normality is important because normal matrices are precisely those to which the spectral theoremSpectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
applies: a matrix A is normal if and only if it can be represented by a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
Λ and a unitary matrix U by the formula
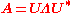
where
The entries λ of diagonal matrix Λ are the eigenvalues of A, and the columns of U are the eigenvectors of A. The matching eigenvalues in Λ come in the same order as the eigenvectors are ordered as columns of U.
Another way of stating the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
is to say that normal matrices are precisely those matrices that can be represented by a diagonal matrix with respect to a properly chosen orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of Cn. Phrased differently: a matrix is normal if and only if its eigenspaces span Cn and are pairwise orthogonal with respect to the standard inner product of Cn.
The spectral theorem for normal matrices can be seen as a special case of the more general result which holds for all square matrices: Schur decomposition
Schur decomposition
In the mathematical discipline of linear algebra, the Schur decomposition or Schur triangulation, named after Issai Schur, is a matrix decomposition.- Statement :...
. In fact, let A be a square matrix. Then by Schur decomposition it is unitary similar to a upper-triangular matrix, say, B. If A is normal, so is B. But then B must be diagonal, for, as noted above, a normal upper-triangular matrix is diagonal.
The spectral theorem permits the classification of normal matrices in terms of their spectra. For example, a normal matrix is unitary if and only if its spectrum is contained in the unit circle of the complex plane. Also, a normal matrix is self-adjoint
Self-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
if and only if its spectrum consists of reals.
In general, the sum or product of two normal matrices need not be normal. However, there is a special case: if A and B are normal with AB = BA, then both AB and A + B are also normal. Furthermore the two are simultaneously diagonalizable, that is: both A and B are made diagonal by the same unitary matrix U. Both UAU* and UBU* are diagonal matrices. In this special case, the columns of U* are eigenvectors of both A and B and form an orthonormal basis in Cn.
Equivalent definitions
It is possible to give a fairly long list of equivalent definitions of a normal matrix. Let A be a n-by-n matrix. Then the following are equivalent:- A is normal.
- A is diagonalizableDiagonalizable matrixIn linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
by a unitary matrix. - The entire space is spanned by some orthonormal set of eigenvectors of A.
-
for every x. -
(That is, the Frobenius norm of A can be computed by the eigenvalues of A.) - The Hermitian part
and skew-HermitianSkew-Hermitian matrixIn linear algebra, a square matrix with complex entries is said to be skew-Hermitian or antihermitian if its conjugate transpose is equal to its negative. That is, the matrix A is skew-Hermitian if it satisfies the relationA^\dagger = -A,\;...
part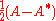
of A commute. -
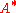is a polynomial (of degree ≤ n − 1) in 
. -
for some unitary matrix U. - U and P commute, where we have the polar decomposition A = UP with a unitary matrix U and some positive semidefinite matrixPositive-definite matrixIn linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
P. - A commutes with some normal matrix N with distinct eigenvalues.
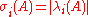for all 
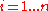where A has singular values 
and eigenvalues 
Some but not all of the above generalize to normal operators on infinite-dimensional Hilbert spaces. For example, a bounded operator satisfying (9) is only quasinormal
Quasinormal operator
In operator theory, quasinormal operators is a class of bounded operators defined by weakening the requirements of a normal operator.Every quasinormal operator is a subnormal operator...
.
The operator norm of a normal matrix N equals the spectral
Spectral radius
In mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
and numerical radii of N. (This fact generalizes to normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
s.) Explicitly, this means:
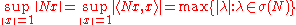
Analogy
It is occasionally useful (but sometimes misleading) to think of the relationships of different kinds of normal matrices as analogous to the relationships between different kinds of complex numbers:- Invertible matrices are analogous to non-zero complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s - The conjugate transposeConjugate transposeIn mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
is analogous to the complex conjugateComplex conjugateIn mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs... - Unitary matrices are analogous to complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s whose absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
is 1 - Hermitian matrices are analogous to real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s - Hermitian positive definite matricesPositive-definite matrixIn linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
are analogous to positive real numbers - Skew Hermitian matricesSkew-Hermitian matrixIn linear algebra, a square matrix with complex entries is said to be skew-Hermitian or antihermitian if its conjugate transpose is equal to its negative. That is, the matrix A is skew-Hermitian if it satisfies the relationA^\dagger = -A,\;...
are analogous to purely imaginary numberImaginary numberAn imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
s
(As a special case, the complex numbers may be embedded in the normal
real matrices by the mapping 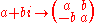, which preserves addition and multiplication. It is easy to check that this embedding respects all of the above analogies.)