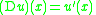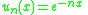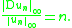In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 — specifically, in operator theory

Operator theory

In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....

 — a densely defined operator is a type of partially defined function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

; in a topological

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

 sense, it is a linear operator that is defined "almost everywhere". Densely defined operators often arise in functional analysis

Functional analysis

Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...

 as operations that one would like to apply to a larger class of objects than those for which they a priori "make sense".

Definition

A linear operator T from one topological vector space

Topological vector space

In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...

, X, to another one, Y, is said to be densely defined if the domain

Domain (mathematics)

In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...

 of T is a dense subset

Dense set

In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...

 of X and the range

Range (mathematics)

In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...

 of T is contained within Y.

Examples

• Consider the space C⁰([0, 1]; R) of all real-valued
  Real number
  In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
  
  , continuous function
  Continuous function
  In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
  
  s defined on the unit interval; let C¹([0, 1]; R) denote the subspace consisting of all continuously differentiable functions
  Smooth function
  In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
  
  . Equip C⁰([0, 1]; R) with the supremum norm ||·||_∞; this makes C⁰([0, 1]; R) into a real Banach space
  Banach space
  In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
  
  . The differentiation operator
  Differential operator
  In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
  
   D given by

is a densely-defined operator from C⁰([0, 1]; R) to itself, defined on the dense subspace C¹([0, 1]; R). Note also that the operator D is an example of an unbounded linear operator, since

This unboundedness causes problems if one wishes to somehow continuously extend the differentiation operator D to the whole of C⁰([0, 1]; R).

• The Paley–Wiener integral, on the other hand, is an example of a continuous extension of a densely-defined operator. In any abstract Wiener space
  Abstract Wiener space
  An abstract Wiener space is a mathematical object in measure theory, used to construct a "decent" measure on an infinite-dimensional vector space. It is named after the American mathematician Norbert Wiener...
  
   i : H → E with adjoint j = i^∗ : E^∗ → H, there is a natural continuous linear operator
  Continuous linear operator
  In functional analysis and related areas of mathematics, a continuous linear operator or continuous linear mapping is a continuous linear transformation between topological vector spaces....
  
   (in fact it is the inclusion, and is an isometry
  Isometry
  In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
  
  ) from j(E^∗) to L²(E, γ; R), under which j(f) ∈ j(E^∗) ⊆ H goes to the equivalence class [f] of f in L²(E, γ; R). It is not hard to show that j(E^∗) is dense in H. Since the above inclusion is continuous, there is a unique continuous linear extension I : H → L²(E, γ; R) of the inclusion j(E^∗) → L²(E, γ; R) to the whole of H. This extension is the Paley–Wiener map.