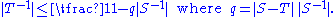Neumann series
Encyclopedia
A Neumann series is a mathematical series
of the form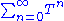
where T is an operator. Hence, Tn is a mathematical notation for n consecutive operations of the operator T. This generalizes the geometric series.
The series is named after the mathematician Carl Neumann
, who used it in 1877 in the context of potential theory
. The Neumann series is used in functional analysis
. It forms the basis of the Liouville-Neumann series
, which is used to solve Fredholm integral equation
s. It is also important when studying the spectrum
of bounded operators.
X. If the Neumann series converges in the operator norm
, then Id – T is invertible and its inverse is the series: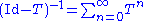 ,
,
where is the identity operator in X.
is the identity operator in X.
One case in which convergence is guaranteed is when X is a Banach space
and |T| < 1 in the operator norm. However, there are also results which give weaker conditions under which the series converges.
' be an invertible operator and let T: B → B' be another operator. If |S – T | < |S–1|–1, then T is also invertible. This follows by writing T as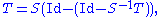
and applying the result in the previous section on the second factor. The norm of T–1 can be bounded by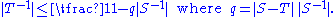
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
of the form
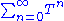
where T is an operator. Hence, Tn is a mathematical notation for n consecutive operations of the operator T. This generalizes the geometric series.
The series is named after the mathematician Carl Neumann
Carl Neumann
Carl Gottfried Neumann was a German mathematician.Neumann was born in Königsberg, Prussia, as the son of the mineralogist, physicist and mathematician Franz Ernst Neumann , who was professor of mineralogy and physics at Königsberg University...
, who used it in 1877 in the context of potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
. The Neumann series is used in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. It forms the basis of the Liouville-Neumann series
Liouville-Neumann series
In mathematics, the Liouville–Neumann series is an infinite series that corresponds to the resolvent formalism technique of solving the Fredholm integral equations in Fredholm theory.-Definition:The Liouville–Neumann series is defined as...
, which is used to solve Fredholm integral equation
Fredholm integral equation
In mathematics, the Fredholm integral equation is an integral equation whose solution gives rise to Fredholm theory, the study of Fredholm kernels and Fredholm operators. The integral equation was studied by Ivar Fredholm.-Equation of the first kind :...
s. It is also important when studying the spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
of bounded operators.
Properties
Suppose that T is a bounded operator on the normed vector spaceNormed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
X. If the Neumann series converges in the operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
, then Id – T is invertible and its inverse is the series:
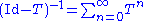 ,
,where
 is the identity operator in X.
is the identity operator in X.One case in which convergence is guaranteed is when X is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
and |T| < 1 in the operator norm. However, there are also results which give weaker conditions under which the series converges.
The set of invertible operators is open
A corollary is that the set of invertible operators between two Banach spaces B and B is open in the topology induced by the operator norm. Indeed, let S : B → B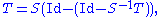
and applying the result in the previous section on the second factor. The norm of T–1 can be bounded by