Fredholm integral equation
Encyclopedia
In mathematics
, the Fredholm integral equation is an integral equation
whose solution gives rise to Fredholm theory
, the study of Fredholm kernel
s and Fredholm operator
s. The integral equation was studied by Ivar Fredholm.
A homogeneous
Fredholm equation of the first kind is written as:
and the problem is, given the continuous kernel function K(t,s), and the function g(t), to find the function f(s).
If the kernel is a function only of the difference of its arguments, namely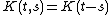
, and the limits of integration are 
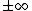, then the right hand side of the equation can be rewritten as a convolution of the functions K and f and therefore the solution will be given by
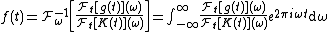
where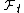
and 
are the direct and inverse Fourier transforms respectively.
Given the kernel K(t,s), and the function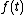
, the problem is typically to find the function 
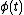. A standard approach to solving this is to use the resolvent formalism
; written as a series, the solution is known as the Liouville-Neumann series
.
. One of the principal results is that the kernel K is a compact operator
, known as the Fredholm operator
. Compactness may be shown by invoking equicontinuity
. As an operator, it has a spectral theory
that can be understood in terms of a discrete spectrum of eigenvalues that tend to 0.
, most notably as the famous spectral concentration problem
popularized by David Slepian
. They also commonly arise in linear forward modeling and inverse problem
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Fredholm integral equation is an integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
whose solution gives rise to Fredholm theory
Fredholm theory
In mathematics, Fredholm theory is a theory of integral equations. In the narrowest sense, Fredholm theory concerns itself with the solution of the Fredholm integral equation. In a broader sense, the abstract structure of Fredholm's theory is given in terms of the spectral theory of Fredholm...
, the study of Fredholm kernel
Fredholm kernel
In mathematics, a Fredholm kernel is a certain type of a kernel on a Banach space, associated with nuclear operators on the Banach space. They are an abstraction of the idea of the Fredholm integral equation and the Fredholm operator, and are one of the objects of study in Fredholm theory....
s and Fredholm operator
Fredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
s. The integral equation was studied by Ivar Fredholm.
Equation of the first kind
Integral equations, most generally, are common and take many specific forms (Fourier, Laplace, Hankel, etc.). They each differ in their kernels (defined below). What is distinctive about Fredholm integral equations is that they are integral equations in which the integration limits are constants (they do not include the variable). This is contrast to Volterra integral equations.A homogeneous
Homogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
Fredholm equation of the first kind is written as:
and the problem is, given the continuous kernel function K(t,s), and the function g(t), to find the function f(s).
If the kernel is a function only of the difference of its arguments, namely
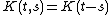, and the limits of integration are 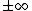, then the right hand side of the equation can be rewritten as a convolution of the functions K and f and therefore the solution will be given by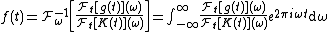where
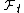and are the direct and inverse Fourier transforms respectively.Equation of the second kind
An inhomogeneous Fredholm equation of the second kind is given asGiven the kernel K(t,s), and the function
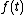, the problem is typically to find the function 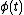. A standard approach to solving this is to use the resolvent formalismResolvent formalism
In mathematics, the resolvent formalism is a technique for applying concepts from complex analysis to the study of the spectrum of operators on Hilbert spaces and more general spaces....
; written as a series, the solution is known as the Liouville-Neumann series
Liouville-Neumann series
In mathematics, the Liouville–Neumann series is an infinite series that corresponds to the resolvent formalism technique of solving the Fredholm integral equations in Fredholm theory.-Definition:The Liouville–Neumann series is defined as...
.
General theory
The general theory underlying the Fredholm equations is known as Fredholm theoryFredholm theory
In mathematics, Fredholm theory is a theory of integral equations. In the narrowest sense, Fredholm theory concerns itself with the solution of the Fredholm integral equation. In a broader sense, the abstract structure of Fredholm's theory is given in terms of the spectral theory of Fredholm...
. One of the principal results is that the kernel K is a compact operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
, known as the Fredholm operator
Fredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
. Compactness may be shown by invoking equicontinuity
Equicontinuity
In mathematical analysis, a family of functions is equicontinuous if all the functions are continuous and they have equal variation over a given neighbourhood, in a precise sense described herein...
. As an operator, it has a spectral theory
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
that can be understood in terms of a discrete spectrum of eigenvalues that tend to 0.
Applications
Fredholm equations arise naturally in the theory of signal processingSignal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, most notably as the famous spectral concentration problem
Spectral concentration problem
The spectral concentration problem in Fourier analysis refers to finding a time sequence whose discrete Fourier transform is maximally localized on a given frequency interval, as measured by the spectral concentration.-Spectral concentration:...
popularized by David Slepian
David Slepian
David S. Slepian was an American mathematician.Born in Pittsburgh, Pennsylvania he studied B.Sc. at University of Michigan before joining the forces in World War II,as Sonic deception officer in the Ghost army....
. They also commonly arise in linear forward modeling and inverse problem
Inverse problem
An inverse problem is a general framework that is used to convert observed measurements into information about a physical object or system that we are interested in...
s.