Fredholm kernel
Encyclopedia
In mathematics
, a Fredholm kernel is a certain type of a kernel on a Banach space
, associated with nuclear operator
s on the Banach space. They are an abstraction of the idea of the Fredholm integral equation
and the Fredholm operator
, and are one of the objects of study in Fredholm theory
. Fredholm kernels are named in honour of Erik Ivar Fredholm
. Much of the abstract theory of Fredholm kernels was developed by Alexander Grothendieck
and published in 1955.
, and let B* be its dual, that is, the space of bounded linear functionals on B. The tensor product
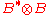has a completion
under the norm
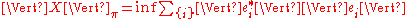
where the infimum
is taken over all finite representations
The completion, under this norm, is often denoted as
and is called the projective topological tensor product
. The elements of this space are called Fredholm kernels.
with
and 
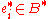such that 
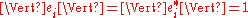and
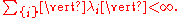
Associated with each such kernel is a linear operator
which has the canonical representation
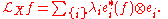
Associated with every Fredholm kernel is a trace, defined as
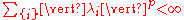
A Fredholm kernel is said to be of order q if q is the infimum
of all
for all p for which it is p-summable.
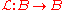is said to be a nuclear operator
if there exists an
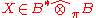such that 
. Such an operator is said to be p-summable and of order q if X is. In general, there may be more than one X associated with such a nuclear operator, and so the trace is not uniquely defined. However, if the order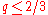 
, then there is a unique trace, as given by a theorem of Grothendieck.
is an operator of order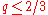 
then a trace may be defined, with
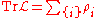
where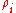
are the eigenvalues of 
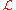. Furthermore, the Fredholm determinant
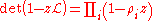
is an entire function
of z. The formula
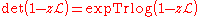
holds as well. Finally, if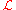
is parameterized by some complex
-valued parameter w, that is,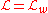
, and the parameterization is holomorphic on some domain, then
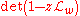
is holomorphic on the same domain.
. In this space, every nuclear operator is of order zero, and is thus of trace-class.
s. A nuclear space
is a Fréchet space where every bounded map of the space to an arbitrary Banach space is nuclear.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Fredholm kernel is a certain type of a kernel on a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, associated with nuclear operator
Nuclear operator
In mathematics, a nuclear operator is roughly a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis .Nuclear operators are essentially the same as trace class operators, though most authors reserve the term "trace...
s on the Banach space. They are an abstraction of the idea of the Fredholm integral equation
Fredholm integral equation
In mathematics, the Fredholm integral equation is an integral equation whose solution gives rise to Fredholm theory, the study of Fredholm kernels and Fredholm operators. The integral equation was studied by Ivar Fredholm.-Equation of the first kind :...
and the Fredholm operator
Fredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
, and are one of the objects of study in Fredholm theory
Fredholm theory
In mathematics, Fredholm theory is a theory of integral equations. In the narrowest sense, Fredholm theory concerns itself with the solution of the Fredholm integral equation. In a broader sense, the abstract structure of Fredholm's theory is given in terms of the spectral theory of Fredholm...
. Fredholm kernels are named in honour of Erik Ivar Fredholm
Erik Ivar Fredholm
Erik Ivar Fredholm was a Swedish mathematician who established the modern theory of integral equations. His 1903 paper in Acta Mathematica is considered to be one of the major landmarks in the establishment of operator theory.The lunar crater Fredholm is named after him.-List of publications:* E.I...
. Much of the abstract theory of Fredholm kernels was developed by Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
and published in 1955.
Definition
Let B be an arbitrary Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, and let B* be its dual, that is, the space of bounded linear functionals on B. The tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
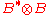has a completionComplete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
under the norm
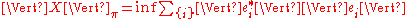
where the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
is taken over all finite representations
The completion, under this norm, is often denoted as
and is called the projective topological tensor product
Topological tensor product
In mathematics, there are usually many different ways to construct a topological tensor product of two topological vector spaces. For Hilbert spaces or nuclear spaces there is a simple well-behaved theory of tensor products , but for general Banach spaces or locally convex topological vector space...
. The elements of this space are called Fredholm kernels.
Properties
Every Fredholm kernel has a representation in the formwith
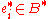and such that 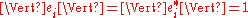and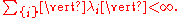Associated with each such kernel is a linear operator
which has the canonical representation
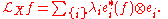
Associated with every Fredholm kernel is a trace, defined as
p-summable kernels
A Fredholm kernel is said to be p-summable if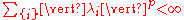A Fredholm kernel is said to be of order q if q is the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of all
for all p for which it is p-summable.Nuclear operators on Banach spaces
An operator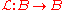 is said to be a nuclear operatorNuclear operator
In mathematics, a nuclear operator is roughly a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis .Nuclear operators are essentially the same as trace class operators, though most authors reserve the term "trace...
if there exists an
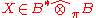such that . Such an operator is said to be p-summable and of order q if X is. In general, there may be more than one X associated with such a nuclear operator, and so the trace is not uniquely defined. However, if the order 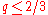, then there is a unique trace, as given by a theorem of Grothendieck.Grothendieck's theorem
If is an operator of order 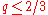then a trace may be defined, with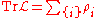where
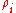are the eigenvalues of 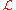. Furthermore, the Fredholm determinantFredholm determinant
In mathematics, the Fredholm determinant is a complex-valued function which generalizes the determinant of a matrix. It is defined for bounded operators on a Hilbert space which differ from the identity operator by a trace-class operator...
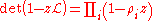
is an entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
of z. The formula
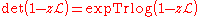
holds as well. Finally, if
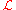is parameterized by some complexComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued parameter w, that is,
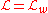, and the parameterization is holomorphic on some domain, then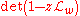is holomorphic on the same domain.
Examples
An important example is the Banach space of holomorphic functions over a domain. In this space, every nuclear operator is of order zero, and is thus of trace-class.Nuclear spaces
The idea of a nuclear operator can be adapted to Fréchet spaceFréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
s. A nuclear space
Nuclear space
In mathematics, a nuclear space is a topological vector space with many of the good properties of finite-dimensional vector spaces. The topology on them can be defined by a family of seminorms whose unit balls decrease rapidly in size...
is a Fréchet space where every bounded map of the space to an arbitrary Banach space is nuclear.