
Topological tensor product
Encyclopedia
In mathematics
, there are usually many different ways to construct a topological tensor product of two topological vector space
s. For Hilbert space
s or nuclear space
s there is a simple well-behaved
theory of tensor product
s (see Tensor product of Hilbert spaces
), but for general Banach space
s or locally convex topological vector space
the theory is notoriously subtle.
The algebraic tensor product of two Hilbert spaces A and B
has a natural positive definite sesquilinear form
induced by the sesquilinear forms of A and B. So in particular it has a natural positive definite quadratic form, and the corresponding completion is a Hilbert space A⊗B, called the (Hilbert space) tensor product of A and B.
If the vectors ai and bj run through orthonormal bases of A and B, then the vectors ai⊗bj form an orthonormal basis of A⊗B.
If A and B are Banach spaces the algebraic tensor product of A and B means the tensor product
of
A and B as vector spaces and is denoted by .
.
The algebraic tensor product consists of all finite sums
consists of all finite sums
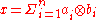
where is a natural number depending on
is a natural number depending on  and
and
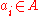 and
and  for
for
 .
.
When A and B are Banach spaces a cross norm p on the algebraic tensor product
is a norm satisfying the conditions

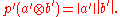
Here a′ and b′ are in the duals of A and B,
and p′ is the dual norm of p. The term reasonable crossnorm is also used for the definition above.
There is a largest cross norm called the projective cross norm, given by
called the projective cross norm, given by
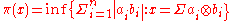
where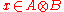 .
.
There is a smallest cross norm called the injective cross norm,given by
called the injective cross norm,given by
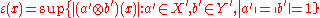
where . Here A′ and B′ mean the topological duals of
. Here A′ and B′ mean the topological duals of
Banach spaces A and B, respectively.
The completions of the algebraic tensor product in these two norms are called
the projective and injective tensor products, and are denoted by
and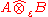 .
.
The norm used for the Hilbert space tensor product is not equal to either of these norms in general.
Some authors denote it by σ, so the Hilbert space tensor product in the section above would be
 .
.
A uniform crossnorm α is an assignment to each pair of Banach spaces of a reasonable crossnorm on
of Banach spaces of a reasonable crossnorm on  so that if
so that if  ,
,  ,
,  ,
,  are arbitrary Banach spaces then for all (continuous linear) operators
are arbitrary Banach spaces then for all (continuous linear) operators 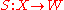 and
and 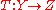 the operator
the operator  is continuous and
is continuous and
 .
.
If A and B are two Banach spaces and α is a uniform cross norm then α defines a reasonable cross norm on the algebraic tensor product . The normed linear space obtained by equipping
. The normed linear space obtained by equipping  with that norm is denoted by
with that norm is denoted by  . The completion of
. The completion of 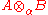 , which is a Banach space, is denoted by
, which is a Banach space, is denoted by 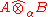 . The value of the norm given by α on
. The value of the norm given by α on  and on the completed tensor product
and on the completed tensor product 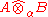 for an element x in
for an element x in 
(or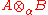 ) is denoted by
) is denoted by  or
or 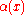 .
.
A uniform crossnorm is said to be finitely generated if, for every pair
is said to be finitely generated if, for every pair 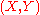 of Banach spaces and every
of Banach spaces and every 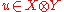 ,
,
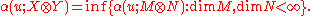
A uniform crossnorm is cofinitely generated if, for every pair
is cofinitely generated if, for every pair 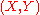 of Banach spaces and every
of Banach spaces and every  ,
,

A tensor norm is defined to be a finitely generated uniform crossnorm.
The projective cross norm and the injective cross norm
and the injective cross norm  defined above are tensor norms
defined above are tensor norms
and they are called the projective tensor norm and the injective tensor norm, respectively.
If A and B are arbitrary Banach spaces and α is an arbitrary uniform cross norm then

on A and on B we can define the corresponding family of cross norms on the algebraic tensor product A⊗B, and by choosing one cross norm from each family we get some cross norms on A⊗B, defining a topology. There are in general an enormous number of ways to do this. The two most important ways are to take all the projective cross norms, or all the injective cross norms. The completions of the resulting topologies on A⊗B are called the projective and injective tensor products, and denoted by A⊗γB and A⊗λB.
There is a natural map from A⊗γB
to A⊗λB.
If A or B is a nuclear space
then the natural map from A⊗γB
to A⊗λB is an isomorphism. Roughly speaking, this means that if A or B is nuclear, then there is only one sensible tensor product of A and B.
This property characterizes nuclear spaces.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, there are usually many different ways to construct a topological tensor product of two topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s. For Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s or nuclear space
Nuclear space
In mathematics, a nuclear space is a topological vector space with many of the good properties of finite-dimensional vector spaces. The topology on them can be defined by a family of seminorms whose unit balls decrease rapidly in size...
s there is a simple well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
theory of tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s (see Tensor product of Hilbert spaces
Tensor product of Hilbert spaces
In mathematics, and in particular functional analysis, the tensor product of Hilbert spaces is a way to extend the tensor product construction so that the result of taking a tensor product of two Hilbert space is another Hilbert space. Roughly speaking, the tensor product is the completion of the...
), but for general Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s or locally convex topological vector space
Locally convex topological vector space
In functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
the theory is notoriously subtle.
Tensor products of Hilbert spaces
The algebraic tensor product of two Hilbert spaces A and B
has a natural positive definite sesquilinear form
Sesquilinear form
In mathematics, a sesquilinear form on a complex vector space V is a map V × V → C that is linear in one argument and antilinear in the other. The name originates from the numerical prefix sesqui- meaning "one and a half"...
induced by the sesquilinear forms of A and B. So in particular it has a natural positive definite quadratic form, and the corresponding completion is a Hilbert space A⊗B, called the (Hilbert space) tensor product of A and B.
If the vectors ai and bj run through orthonormal bases of A and B, then the vectors ai⊗bj form an orthonormal basis of A⊗B.
Cross norms and tensor products of Banach spaces
We shall use the notation from in this section. The obvious way to define the tensor product of two Banach spaces A and B is to copy the method for Hilbert spaces: define a norm on the algebraic tensor product, then take the completion in this norm. The problem is that there is more than one natural way to define a norm on the tensor product.If A and B are Banach spaces the algebraic tensor product of A and B means the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of
A and B as vector spaces and is denoted by
 .
.The algebraic tensor product
 consists of all finite sums
consists of all finite sums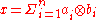
where
 is a natural number depending on
is a natural number depending on  and
and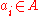 and
and  for
for .
.When A and B are Banach spaces a cross norm p on the algebraic tensor product

is a norm satisfying the conditions

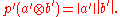
Here a′ and b′ are in the duals of A and B,
and p′ is the dual norm of p. The term reasonable crossnorm is also used for the definition above.
There is a largest cross norm
 called the projective cross norm, given by
called the projective cross norm, given by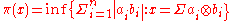
where
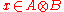 .
.There is a smallest cross norm
 called the injective cross norm,given by
called the injective cross norm,given by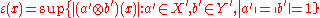
where
 . Here A′ and B′ mean the topological duals of
. Here A′ and B′ mean the topological duals ofBanach spaces A and B, respectively.
The completions of the algebraic tensor product in these two norms are called
the projective and injective tensor products, and are denoted by

and
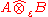 .
.The norm used for the Hilbert space tensor product is not equal to either of these norms in general.
Some authors denote it by σ, so the Hilbert space tensor product in the section above would be
 .
.A uniform crossnorm α is an assignment to each pair
 of Banach spaces of a reasonable crossnorm on
of Banach spaces of a reasonable crossnorm on  so that if
so that if  ,
,  ,
,  ,
,  are arbitrary Banach spaces then for all (continuous linear) operators
are arbitrary Banach spaces then for all (continuous linear) operators 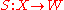 and
and 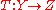 the operator
the operator  is continuous and
is continuous and .
.If A and B are two Banach spaces and α is a uniform cross norm then α defines a reasonable cross norm on the algebraic tensor product
 . The normed linear space obtained by equipping
. The normed linear space obtained by equipping  with that norm is denoted by
with that norm is denoted by  . The completion of
. The completion of 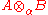 , which is a Banach space, is denoted by
, which is a Banach space, is denoted by 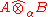 . The value of the norm given by α on
. The value of the norm given by α on  and on the completed tensor product
and on the completed tensor product 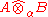 for an element x in
for an element x in 
(or
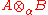 ) is denoted by
) is denoted by  or
or 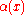 .
.A uniform crossnorm
 is said to be finitely generated if, for every pair
is said to be finitely generated if, for every pair 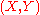 of Banach spaces and every
of Banach spaces and every 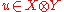 ,
,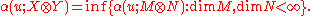
A uniform crossnorm
 is cofinitely generated if, for every pair
is cofinitely generated if, for every pair 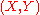 of Banach spaces and every
of Banach spaces and every  ,
,
A tensor norm is defined to be a finitely generated uniform crossnorm.
The projective cross norm
 and the injective cross norm
and the injective cross norm  defined above are tensor norms
defined above are tensor normsand they are called the projective tensor norm and the injective tensor norm, respectively.
If A and B are arbitrary Banach spaces and α is an arbitrary uniform cross norm then

Tensor products of locally convex topological vector spaces
The topologies of locally convex topological vector spaces A and B are given by families of seminorms. For each choice of seminormon A and on B we can define the corresponding family of cross norms on the algebraic tensor product A⊗B, and by choosing one cross norm from each family we get some cross norms on A⊗B, defining a topology. There are in general an enormous number of ways to do this. The two most important ways are to take all the projective cross norms, or all the injective cross norms. The completions of the resulting topologies on A⊗B are called the projective and injective tensor products, and denoted by A⊗γB and A⊗λB.
There is a natural map from A⊗γB
to A⊗λB.
If A or B is a nuclear space
Nuclear space
In mathematics, a nuclear space is a topological vector space with many of the good properties of finite-dimensional vector spaces. The topology on them can be defined by a family of seminorms whose unit balls decrease rapidly in size...
then the natural map from A⊗γB
to A⊗λB is an isomorphism. Roughly speaking, this means that if A or B is nuclear, then there is only one sensible tensor product of A and B.
This property characterizes nuclear spaces.
See also
- Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, Fréchet spaceFréchet spaceIn functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
, locally convex topological vector spaceLocally convex topological vector spaceIn functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
, Nuclear spaceNuclear spaceIn mathematics, a nuclear space is a topological vector space with many of the good properties of finite-dimensional vector spaces. The topology on them can be defined by a family of seminorms whose unit balls decrease rapidly in size... - Tensor product of Hilbert spacesTensor product of Hilbert spacesIn mathematics, and in particular functional analysis, the tensor product of Hilbert spaces is a way to extend the tensor product construction so that the result of taking a tensor product of two Hilbert space is another Hilbert space. Roughly speaking, the tensor product is the completion of the...
- Fredholm kernelFredholm kernelIn mathematics, a Fredholm kernel is a certain type of a kernel on a Banach space, associated with nuclear operators on the Banach space. They are an abstraction of the idea of the Fredholm integral equation and the Fredholm operator, and are one of the objects of study in Fredholm theory....
- Projective topology

