
Tensor product of Hilbert spaces
Encyclopedia
In mathematics
, and in particular functional analysis
, the tensor product of Hilbert space
s is a way to extend the tensor product
construction so that the result of taking a tensor product of two Hilbert space is another Hilbert space. Roughly speaking, the tensor product is the completion of the ordinary tensor product. This is a special case of a topological tensor product
.
 and
and  , respectively. Construct the tensor product of H1 and H2 as vector spaces as explained in the article on tensor product
, respectively. Construct the tensor product of H1 and H2 as vector spaces as explained in the article on tensor product
s. We can turn this vector space tensor product into an inner product space
by defining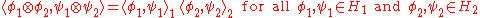
and extending by linearity. That this inner product is the natural one is justified by the identification of scalar-valued bilinear maps on H1 × H2 and linear functionals on their vector space tensor product. Finally, take the completion under this inner product. The resulting Hilbert space is the tensor product of H1 and H2.
 the rank one operator
the rank one operator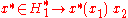
from H1∗ to H2, and this extends to a linear identification between and the space of finite rank operators from H1∗ to H2.
and the space of finite rank operators from H1∗ to H2.
The finite rank operators are embedded in the Hilbert space HS(H1∗, H2) of Hilbert-Schmidt operators from H1∗ to H2. The scalar product in HS(H1∗, H2) is given by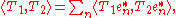
where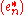 is an arbitrary orthonormal basis of H1∗.
is an arbitrary orthonormal basis of H1∗.
Under the preceding identification, one can define the Hilbertian tensor product of H1 and H2, that is isometrically and linearly isomorphic to HS(H1∗, H2).
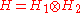 is characterized by the following universal property
is characterized by the following universal property
:
As with any universal property, this characterizes the tensor product H up to isomorphism. The same universal property, with obvious modifications, also applies for the tensor product of any finite number of Hilbert spaces.
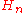 is a collection of Hilbert spaces and
is a collection of Hilbert spaces and 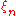 is a collection of unit vectors in these Hilbert spaces then the incomplete tensor product (or Guichardet tensor product) is the
is a collection of unit vectors in these Hilbert spaces then the incomplete tensor product (or Guichardet tensor product) is the 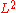 completion of the set of all finite linear combinations of simple tensor vectors
completion of the set of all finite linear combinations of simple tensor vectors  where all but finitely many of the
where all but finitely many of the 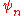 's equal the corresponding
's equal the corresponding 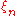 .
.
 be the von Neumann algebra of bounded operators on
be the von Neumann algebra of bounded operators on 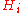 for
for  . Then the von Neumann tensor product of the von Neumann algebras is the strong completion of the set of all finite linear combinations of simple tensor products
. Then the von Neumann tensor product of the von Neumann algebras is the strong completion of the set of all finite linear combinations of simple tensor products  where
where  for
for  . This is exactly equal to the von Neumann algebra of bounded operators of
. This is exactly equal to the von Neumann algebra of bounded operators of  . Unlike for Hilbert spaces, one may take infinite tensor products of von Neumann algebras, and for that matter
. Unlike for Hilbert spaces, one may take infinite tensor products of von Neumann algebras, and for that matter 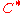 -algebras of operators, without defining reference states. This is one advantage of the "algebraic" method in quantum statistical mechanics.
-algebras of operators, without defining reference states. This is one advantage of the "algebraic" method in quantum statistical mechanics.
{φk} and {ψl}, respectively, then {φk ⊗ ψl} is an orthonormal basis for H1 ⊗ H2. In particular, the Hilbert dimension of the tensor product is the product (as cardinal number
s) of the Hilbert dimensions.
Given two measure spaces X and Y, with measures μ and ν respectively, one may look at L
2(X × Y), the space of functions on X × Y that are square integrable with respect to the product measure μ × ν. If f is a square integrable function on X, and g is a square integrable function on Y, then we can define a function h on X × Y by h(x,y) = f(x) g(y). The definition of the product measure ensures that all functions of this form are square integrable, so this defines a bilinear
mapping L2(X) × L2(Y) → L2(X × Y). Linear combination
s of functions of the form f(x) g(y) are also in L2(X × Y). It turns out that the set of linear combinations is in fact dense in L2(X × Y), if L2(X) and L2(Y) are separable. This shows that L2(X) ⊗ L2(Y) is isomorphic to L2(X × Y), and it also explains why we need to take the completion in the construction of the Hilbert space tensor product.
Similarly, we can show that L2(X; H), denoting the space of square integrable functions X → H, is isomorphic to L2(X) ⊗ H if this space is separable. The isomorphism maps f(x) ⊗ φ ∈ L2(X) ⊗ H to f(x)φ ∈ L2(X; H). We can combine this with the previous example and conclude that L2(X) ⊗ L2(Y) and L2(X × Y) are both isomorphic to L2(X; L2(Y)).
Tensor products of Hilbert spaces arise often in quantum mechanics
. If some particle is described by the Hilbert space H1, and another particle is described by H2, then the system consisting of both particles is described by the tensor product of H1 and H2. For example, the state space of a quantum harmonic oscillator
is L2(R), so the state space of two oscillators is L2(R) ⊗ L2(R), which is isomorphic to L2(R2). Therefore, the two-particle system is described by wave functions of the form φ(x1, x2). A more intricate example is provided by the Fock space
s, which describe a variable number of particles.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and in particular functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the tensor product of Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s is a way to extend the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
construction so that the result of taking a tensor product of two Hilbert space is another Hilbert space. Roughly speaking, the tensor product is the completion of the ordinary tensor product. This is a special case of a topological tensor product
Topological tensor product
In mathematics, there are usually many different ways to construct a topological tensor product of two topological vector spaces. For Hilbert spaces or nuclear spaces there is a simple well-behaved theory of tensor products , but for general Banach spaces or locally convex topological vector space...
.
Definition
Since Hilbert spaces have inner products, one would like to introduce an inner product, and therefore a topology, on the tensor product that arise naturally from those of the factors. Let H1 and H2 be two Hilbert spaces with inner products and
and  , respectively. Construct the tensor product of H1 and H2 as vector spaces as explained in the article on tensor product
, respectively. Construct the tensor product of H1 and H2 as vector spaces as explained in the article on tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s. We can turn this vector space tensor product into an inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
by defining
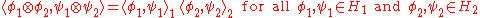
and extending by linearity. That this inner product is the natural one is justified by the identification of scalar-valued bilinear maps on H1 × H2 and linear functionals on their vector space tensor product. Finally, take the completion under this inner product. The resulting Hilbert space is the tensor product of H1 and H2.
Explicit construction
The tensor product can also be defined without appealing to the metric space completion. If H1 and H2 are two Hilbert spaces, one associates to every simple tensor product the rank one operator
the rank one operator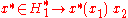
from H1∗ to H2, and this extends to a linear identification between
 and the space of finite rank operators from H1∗ to H2.
and the space of finite rank operators from H1∗ to H2.The finite rank operators are embedded in the Hilbert space HS(H1∗, H2) of Hilbert-Schmidt operators from H1∗ to H2. The scalar product in HS(H1∗, H2) is given by
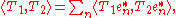
where
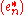 is an arbitrary orthonormal basis of H1∗.
is an arbitrary orthonormal basis of H1∗.Under the preceding identification, one can define the Hilbertian tensor product of H1 and H2, that is isometrically and linearly isomorphic to HS(H1∗, H2).
Universal property
The Hilbert tensor product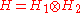 is characterized by the following universal property
is characterized by the following universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
:
- There is a weakly Hilbert-Schmidt mapping p : H1 × H2 → H such that, given any weakly Hilbert-Schmidt mapping L : H1 × H2 → K to a Hilbert space K, there is a unique bounded operator T from H to K such that L = Tp.
As with any universal property, this characterizes the tensor product H up to isomorphism. The same universal property, with obvious modifications, also applies for the tensor product of any finite number of Hilbert spaces.
Infinite tensor products
If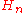 is a collection of Hilbert spaces and
is a collection of Hilbert spaces and 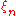 is a collection of unit vectors in these Hilbert spaces then the incomplete tensor product (or Guichardet tensor product) is the
is a collection of unit vectors in these Hilbert spaces then the incomplete tensor product (or Guichardet tensor product) is the 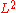 completion of the set of all finite linear combinations of simple tensor vectors
completion of the set of all finite linear combinations of simple tensor vectors  where all but finitely many of the
where all but finitely many of the 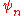 's equal the corresponding
's equal the corresponding 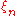 .
.Operator algebras
Let be the von Neumann algebra of bounded operators on
be the von Neumann algebra of bounded operators on 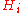 for
for  . Then the von Neumann tensor product of the von Neumann algebras is the strong completion of the set of all finite linear combinations of simple tensor products
. Then the von Neumann tensor product of the von Neumann algebras is the strong completion of the set of all finite linear combinations of simple tensor products  where
where  for
for  . This is exactly equal to the von Neumann algebra of bounded operators of
. This is exactly equal to the von Neumann algebra of bounded operators of  . Unlike for Hilbert spaces, one may take infinite tensor products of von Neumann algebras, and for that matter
. Unlike for Hilbert spaces, one may take infinite tensor products of von Neumann algebras, and for that matter 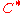 -algebras of operators, without defining reference states. This is one advantage of the "algebraic" method in quantum statistical mechanics.
-algebras of operators, without defining reference states. This is one advantage of the "algebraic" method in quantum statistical mechanics.Properties
If H1 and H2 have orthonormal basesOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
{φk} and {ψl}, respectively, then {φk ⊗ ψl} is an orthonormal basis for H1 ⊗ H2. In particular, the Hilbert dimension of the tensor product is the product (as cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s) of the Hilbert dimensions.
Examples and applications
The following examples show how tensor products arise naturally.Given two measure spaces X and Y, with measures μ and ν respectively, one may look at L
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
2(X × Y), the space of functions on X × Y that are square integrable with respect to the product measure μ × ν. If f is a square integrable function on X, and g is a square integrable function on Y, then we can define a function h on X × Y by h(x,y) = f(x) g(y). The definition of the product measure ensures that all functions of this form are square integrable, so this defines a bilinear
Bilinear
Bilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
mapping L2(X) × L2(Y) → L2(X × Y). Linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s of functions of the form f(x) g(y) are also in L2(X × Y). It turns out that the set of linear combinations is in fact dense in L2(X × Y), if L2(X) and L2(Y) are separable. This shows that L2(X) ⊗ L2(Y) is isomorphic to L2(X × Y), and it also explains why we need to take the completion in the construction of the Hilbert space tensor product.
Similarly, we can show that L2(X; H), denoting the space of square integrable functions X → H, is isomorphic to L2(X) ⊗ H if this space is separable. The isomorphism maps f(x) ⊗ φ ∈ L2(X) ⊗ H to f(x)φ ∈ L2(X; H). We can combine this with the previous example and conclude that L2(X) ⊗ L2(Y) and L2(X × Y) are both isomorphic to L2(X; L2(Y)).
Tensor products of Hilbert spaces arise often in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. If some particle is described by the Hilbert space H1, and another particle is described by H2, then the system consisting of both particles is described by the tensor product of H1 and H2. For example, the state space of a quantum harmonic oscillator
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
is L2(R), so the state space of two oscillators is L2(R) ⊗ L2(R), which is isomorphic to L2(R2). Therefore, the two-particle system is described by wave functions of the form φ(x1, x2). A more intricate example is provided by the Fock space
Fock space
The Fock space is an algebraic system used in quantum mechanics to describe quantum states with a variable or unknown number of particles. It is named after V. A...
s, which describe a variable number of particles.

