Fredholm operator
Encyclopedia
In mathematics
, a Fredholm operator is an operator that arises in the Fredholm theory
of integral equation
s. It is named in honour of Erik Ivar Fredholm
.
A Fredholm operator is a bounded linear operator between two Banach space
s whose kernel
and cokernel
are finite-dimensional and whose range
is closed. (The last condition is actually redundant.) Equivalently, an operator T : X → Y is Fredholm if it is invertible modulo
compact operator
s, i.e., if there exists a bounded linear operator
such that
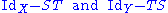
are compact operators on X and Y respectively.
The index of a Fredholm operator is
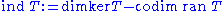
or equivalently,
see dimension
, kernel
, codimension
, range, and cokernel.
. More precisely, when T0 is Fredholm from X to Y, there exists ε > 0 such that every T in L(X, Y) with ||T − T0|| < ε is Fredholm, with the same index as that of T0.
When T is Fredholm from X to Y and U Fredholm from Y to Z, then the composition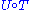
is Fredholm from X to Z and
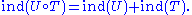
When T is Fredholm, the transpose (or adjoint) operator is Fredholm from to , and . When X and Y are Hilbert spaces
, the same conclusion holds for the Hermitian adjoint
T∗.
When T is Fredholm and K a compact operator, then T + K is Fredholm. The index of T remains constant under compact perturbations of T. This follows from the fact that the index i(s) of is an integer defined for every s in [0, 1], and i(s) is locally constant, hence i(1) = i(0).
Invariance by perturbation is true for larger classes than the class of compact operators. For example, when T is Fredholm and S a strictly singular operator, then T + S is Fredholm with the same index. A bounded linear operator S from X to Y is strictly singular when its restriction to any infinite dimensional subspace X0 of X fails to be an into isomorphism, that is:
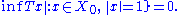
with an orthonormal basis {en} indexed by the non negative integers. The (right) shift operator
S on H is defined by
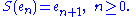
This operator S is injective (actually, isometric) and has a closed range of codimension 1, hence S is Fredholm with ind(S) = −1. The powers Sk, k ≥ 0, are Fredholm with index −k. The adjoint S∗ is the left shift,
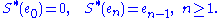
The left shift S∗ is Fredholm with index 1.
If H is the classical Hardy space
H2(T) on the unit circle T in the complex plane, then the shift operator with respect to the orthonormal basis of complex exponentials
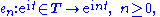
is the multiplication operator Mφ with the function φ = e1. More generally, let φ be a complex continuous function on T that does not vanish on T, and let Tφ denote the Toeplitz operator
with symbol φ, equal to multiplication by φ followed by the orthogonal projection P from L2(T) onto H2(T):
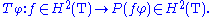
Then Tφ is a Fredholm operator on H2(T), with index related to the winding number
around 0 of the closed path : the index of Tφ, as defined in this article, is the opposite of this winding number.
An elliptic operator
can be extended to a Fredholm operator. The use of Fredholm operators in partial differential equation
s is an abstract form of the parametrix
method.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Fredholm operator is an operator that arises in the Fredholm theory
Fredholm theory
In mathematics, Fredholm theory is a theory of integral equations. In the narrowest sense, Fredholm theory concerns itself with the solution of the Fredholm integral equation. In a broader sense, the abstract structure of Fredholm's theory is given in terms of the spectral theory of Fredholm...
of integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
s. It is named in honour of Erik Ivar Fredholm
Erik Ivar Fredholm
Erik Ivar Fredholm was a Swedish mathematician who established the modern theory of integral equations. His 1903 paper in Acta Mathematica is considered to be one of the major landmarks in the establishment of operator theory.The lunar crater Fredholm is named after him.-List of publications:* E.I...
.
A Fredholm operator is a bounded linear operator between two Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s whose kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
and cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
are finite-dimensional and whose range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
is closed. (The last condition is actually redundant.) Equivalently, an operator T : X → Y is Fredholm if it is invertible modulo
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
compact operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
s, i.e., if there exists a bounded linear operator
such that
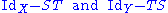
are compact operators on X and Y respectively.
The index of a Fredholm operator is
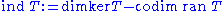
or equivalently,
see dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
, kernel
Null space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
, codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
, range, and cokernel.
Properties
The set of Fredholm operators from X to Y is open in the Banach space L(X, Y) of bounded linear operators, equipped with the operator normOperator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
. More precisely, when T0 is Fredholm from X to Y, there exists ε > 0 such that every T in L(X, Y) with ||T − T0|| < ε is Fredholm, with the same index as that of T0.
When T is Fredholm from X to Y and U Fredholm from Y to Z, then the composition
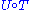is Fredholm from X to Z and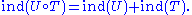When T is Fredholm, the transpose (or adjoint) operator is Fredholm from to , and . When X and Y are Hilbert spaces
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, the same conclusion holds for the Hermitian adjoint
Hermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
T∗.
When T is Fredholm and K a compact operator, then T + K is Fredholm. The index of T remains constant under compact perturbations of T. This follows from the fact that the index i(s) of is an integer defined for every s in [0, 1], and i(s) is locally constant, hence i(1) = i(0).
Invariance by perturbation is true for larger classes than the class of compact operators. For example, when T is Fredholm and S a strictly singular operator, then T + S is Fredholm with the same index. A bounded linear operator S from X to Y is strictly singular when its restriction to any infinite dimensional subspace X0 of X fails to be an into isomorphism, that is:
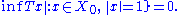
Examples
Let H be a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
with an orthonormal basis {en} indexed by the non negative integers. The (right) shift operator
Shift operator
In mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
S on H is defined by
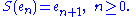
This operator S is injective (actually, isometric) and has a closed range of codimension 1, hence S is Fredholm with ind(S) = −1. The powers Sk, k ≥ 0, are Fredholm with index −k. The adjoint S∗ is the left shift,
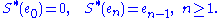
The left shift S∗ is Fredholm with index 1.
If H is the classical Hardy space
Hardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
H2(T) on the unit circle T in the complex plane, then the shift operator with respect to the orthonormal basis of complex exponentials
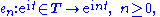
is the multiplication operator Mφ with the function φ = e1. More generally, let φ be a complex continuous function on T that does not vanish on T, and let Tφ denote the Toeplitz operator
Toeplitz operator
In operator theory, a Toeplitz operator is the compression of a multiplication operator on the circle to the Hardy space.- Details :Let S1 be the circle, with the standard Lebesgue measure, and L2 be the Hilbert space of square-integrable functions. A bounded measurable function g on S1 defines a...
with symbol φ, equal to multiplication by φ followed by the orthogonal projection P from L2(T) onto H2(T):
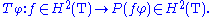
Then Tφ is a Fredholm operator on H2(T), with index related to the winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
around 0 of the closed path : the index of Tφ, as defined in this article, is the opposite of this winding number.
Applications
The Atiyah-Singer index theorem gives a topological characterization of the index of certain operators on manifolds.An elliptic operator
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
can be extended to a Fredholm operator. The use of Fredholm operators in partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s is an abstract form of the parametrix
Parametrix
In mathematics, and specifically the field of partial differential equations , a parametrix is an approximation to a fundamental solution of a PDE, and is essentially an approximate inverse to a differential operator....
method.