Spectral concentration problem - AbsoluteAstronomy.com

The spectral concentration problem in Fourier analysis refers to finding a time sequence whose discrete Fourier transform

Discrete Fourier transform

In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...

is maximally localized on a given frequency

Frequency

Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...

interval, as measured by the spectral concentration.

Spectral concentration

The discrete-time Fourier transform

Discrete-time Fourier transform

In mathematics, the discrete-time Fourier transform is one of the specific forms of Fourier analysis. As such, it transforms one function into another, which is called the frequency domain representation, or simply the "DTFT", of the original function . But the DTFT requires an input function...

(DTFT) U(f) of a finite series

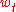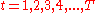is defined as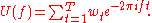

In the following, the sampling interval will be taken as Δt = 1, and hence the frequency interval as
f ∈ [-½,½]. U(f) is a periodic function

Periodic function

In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...

with a period 1.

For a given frequency W such that 0<W<½, the spectral concentration

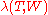of U(f) on the interval [-W,W] is defined as the ratio of power of U(f) contained in the frequency band [-W,W] to the power of U(f) contained in the entire frequency band [-½,½]. That is,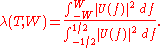

It can be shown that U(f) has only isolated zeros and hence

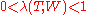(see [1]). Thus, the spectral concentration is strictly less than one, and there is no finite sequence

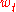for which the DTFT can be confined to a band [-W,W] and made to vanish outside this band.

Statement of the problem

Among all sequences

Séquences

Séquences is a French-language film magazine originally published in Montreal, Quebec by the Commission des ciné-clubs du Centre catholique du cinéma de Montréal, a Roman Catholic film society. Founded in 1955, the publication was edited for forty years by Léo Bonneville, a member of the Clerics...

for a given T and W, is there a sequence for which the spectral concentration is maximum? In other words, is there a sequence for which the sidelobe energy outside a frequency band [-W,W] is minimum?

The answer is yes; such a sequence indeed exists and can be found by optimizing

. Thus maximising the power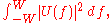

subject to the constraint that the total power is fixed, say

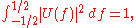
leads to the following equation satisfied by the optimal sequence

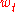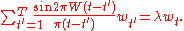
This is an eigenvalue equation for a symmetric matrix

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

given by

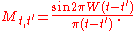
It can be shown that this matrix is positive-definite, hence all the eigenvalues of
this matrix lie between 0 and 1. The largest eigenvalue of the above equation corresponds to the largest possible spectral concentration; the corresponding eigenvector is the required optimal sequence

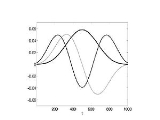
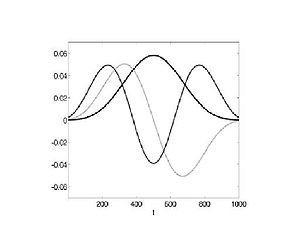
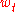. This sequence is called a 0^th–order Slepian sequence (also known as a discrete prolate spheroidal sequence, or DPSS), which is a unique taper with maximally suppressed sidelobes.

It turns out that the number of dominant eigenvalues of the matrix M that are close to 1, corresponds to N=2WT called as Shannon number

Shannon number

The Shannon number, named after Claude Shannon, is an estimated lower bound on the game-tree complexity of chess. Shannon calculated it as an aside in his 1950 paper "Programming a Computer for Playing Chess"...

. If the eigenvectors

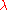are arranged in decreasing order (i.e,

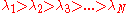), then the eigenvector corresponding to

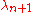is called n^th–order Slepian sequence (DPSS) (0≤n≤N-1). This n^th–order taper also offers the best sidelobe suppression and is pairwise orthogonal to the Slepian sequences of previous orders

. These lower order Slepian sequences form
the basis for spectral estimation by multitaper

Multitaper

In signal processing, the multitaper method is a technique developed by David J. Thomson to estimate the power spectrum SX of a stationary ergodic finite-variance random process X, given a finite contiguous realization of X as data....

method.

Not limited to time series, the spectral concentration problem can be reformulated to apply on the surface of the sphere by using spherical harmonics

Spherical harmonics

In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...

, for applications in geophysics

Geophysics

Geophysics is the physics of the Earth and its environment in space; also the study of the Earth using quantitative physical methods. The term geophysics sometimes refers only to the geological applications: Earth's shape; its gravitational and magnetic fields; its internal structure and...

and cosmology

Cosmology

Cosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...

among others.

Spectral concentration

Statement of the problem

See also