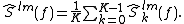In signal processing

Signal processing

Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...

, the multitaper method is a technique developed by David J. Thomson

David J. Thomson

Dr. David J. Thomson is a Professor in the Department of Mathematics and Statistics, and a Canada Research Chair in Statistics and Signal Processing...

 to estimate the power spectrum S_X of a stationary

Stationary process

In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...

 ergodic finite-variance random process X, given a finite contiguous realization

Realization

realization and realisation may be:* Realization , a sport climbing route in Ceüse, France* Realization , the pricing of security at market value* Realization , an actually observed value of random variable...

 of X as data.

Motivation

The multitaper method overcomes some of the limitations of conventional Fourier analysis. When applying the Fourier transform to extract spectral information from a signal, we assume that each Fourier coefficient is a reliable representation of the amplitude and relative phase of the corresponding component frequency. This assumption, however, is not always valid. For instance, a single trial represents only one noisy realization of the underlying process of interest. A comparable situation arises in statistics when estimating measures of central tendency

Mean

In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....

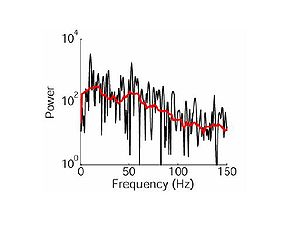
 i.e., it is bad practice to estimate qualities of a population using individuals or very small samples. Likewise, a single sample of a process does not necessarily provide a reliable estimate of its spectral properties. Moreover, the naive power spectral density obtained from the signal's Fourier transform

Fourier transform

In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...

 is a biased estimate of the true spectral content.

These problems are often overcome by averaging over many realizations of the same event. However, this method is unreliable with small data sets and undesirable when one does not wish to attenuate signal components that vary across trials. Instead of ensemble averaging, the multitaper method reduces estimation bias by obtaining multiple independent estimates from the same sample. Each data taper is multiplied element-wise by the signal to provide a windowed trial from which one estimates the power at each component frequency. As each taper is pairwise orthogonal to all other tapers, the windowed signals provide statistically independent estimates of the underlying spectrum. The final spectrum is obtained by averaging over all the tapered spectra. Thomson chose as tapers the Slepian or discrete prolate spheroidal sequences since these tapers are mutually orthogonal and possess desirable spectral concentration properties (see the section on Slepian sequences). In practice, a weighted average is often used to compensate for increased energy loss at higher order tapers.

The method

Consider a p-dimensional zero mean stationary stochastic process

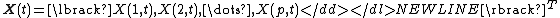
Here T denotes the matrix transposition. In neurophysiology

Neurophysiology

Neurophysiology is a part of physiology. Neurophysiology is the study of nervous system function...

 for example, p refers to the total number of channels and
hence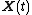 can represent simultaneous measurement of
electrical activity of those p channels. Let the sampling interval
between observations be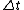 , so that the Nyquist frequency
is .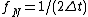

The multitaper spectral estimator utilizes several different data tapers which are orthogonal to each other. The multitaper cross-spectral estimator between channel l and m is the average of K direct cross-spectral estimators between the same pair of channels (l and m) and hence takes the form

Here,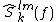 (for 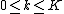) is the k^th direct cross spectral estimator between channel l and m and is given by

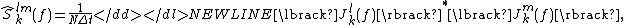
where

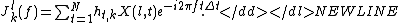
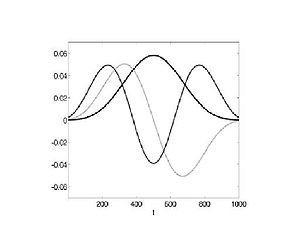
The Slepian sequences

The sequence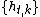 is the data taper for the
k^th direct cross-spectral estimator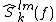 and is chosen as follows:

We choose a set of K orthogonal data tapers such that each one provides a good protection against leakage. These are given by the Slepian sequences, after David Slepian

David Slepian

David S. Slepian was an American mathematician.Born in Pittsburgh, Pennsylvania he studied B.Sc. at University of Michigan before joining the forces in World War II,as Sonic deception officer in the Ghost army....

 (also known in literature as discrete prolate spheroidal sequences or DPSS for short) with parameter W and orders k = 0 to K − 1. The maximum order K is chosen to be less than the Shannon number . The quantity 2W defines the resolution bandwidth for the Spectral concentration problem

Spectral concentration problem

The spectral concentration problem in Fourier analysis refers to finding a time sequence whose discrete Fourier transform is maximally localized on a given frequency interval, as measured by the spectral concentration.-Spectral concentration:...

 and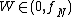 . When l = m, we get the multitaper estimator for the auto-spectrum of the l^th channel.

Applications of multitaper method

This technique is currently used in the spectral analysis

Spectral analysis

Spectral analysis or Spectrum analysis may refer to:* Spectrum analysis in chemistry and physics, a method of analyzing the chemical properties of matter from bands in their visible spectrum...

 toolkit of Chronux

Chronux

Chronux is an open-source software package developed for the loading, visualization and analysis of a variety of modalities / formats of neurobiological time series data...

. An extensive treatment about the application of this method to analyze multi-trial, multi-channel data generated in Neuroscience

Neuroscience

Neuroscience is the scientific study of the nervous system. Traditionally, neuroscience has been seen as a branch of biology. However, it is currently an interdisciplinary science that collaborates with other fields such as chemistry, computer science, engineering, linguistics, mathematics,...

 experiments, Biomedical Engineering

Biomedical engineering

Biomedical Engineering is the application of engineering principles and design concepts to medicine and biology. This field seeks to close the gap between engineering and medicine: It combines the design and problem solving skills of engineering with medical and biological sciences to improve...

 and others can be found here. Not limited to time series, the multitaper method can be reformulated for spectral estimation on the sphere using spherical harmonics

Spherical harmonics

In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...

 for applications in geophysics

Geophysics

Geophysics is the physics of the Earth and its environment in space; also the study of the Earth using quantitative physical methods. The term geophysics sometimes refers only to the geological applications: Earth's shape; its gravitational and magnetic fields; its internal structure and...

 and cosmology

Cosmology

Cosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...

among others.

External links

• http://www.mast.queensu.ca/~djt Website of David J. Thomson
• http://sourceforge.net/projects/mtpsd/ C++ library and Octave dynamical extension
• http://www.atmos.ucla.edu/tcd/ssa/guide/mann/mann.html Documentation on the multitaper method from the SSA-MTM Toolkit implementation
• http://wwwprof.uniandes.edu.co/~gprieto/software/mwlib.html Fortran 90 library with additional multivariate applications
• http://code.google.com/p/pymutt/ Python module

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.